Calcul de limite en 0, avec ln
Colle de mathématiques
Sujet de colle de maths:- DLDéveloppements limités
Énoncé du sujet
Déterminer la limite en 0 de
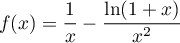
Correction
![\[\ln(1+x)=x-\dfrac{x^2}2+o\left( x^2\rp\]](/Generateur-Devoirs/Colles/DL/DL-limite-ln_c/1.png)
et donc,
![\[\begin{array}{ll}
f(x)&=\dfrac1x-\dfrac{\ln(1+x)}{x^2}\\[1em]
&=\dfrac1x-\dfrac1{x^2}\left( x-\dfrac{x^2}2+o\left( x^2\rp\rp\\[1em]
&=\dfrac12+o(1)
\enar\]](/Generateur-Devoirs/Colles/DL/DL-limite-ln_c/2.png)
ce qui montre que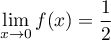
.
Correction
On a, en 0et donc,
ce qui montre que
.
Tag:DL
Autres sujets au hasard:
Voir aussi: