Calcul de limite: composée ln et sin

Colle de mathématiques

Sujet de colle de maths:

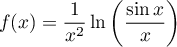
Déterminer la limite en 0 de: $f(x)=\dfrac{1}{x^2}\ln\lp\dfrac{\sin x}{x}\rp$

Correction

En 0 on a

$\sin(x)=x-\dfrac{x^3}{6}+o\left( x^3\rp$

et donc,

$f(x)=\dfrac{1}{x^2}\ln\lp\dfrac{\sin x}{x}\right) =\dfrac1{x^2}\ln\lp1-\dfrac{x^2}6+o\lp x^2\rp\rp$

puis en utilisant le développement limité du logarithme en 0,

$f(x)=\dfrac1{x^2}\left( -\dfrac{x^2}6+o\left( x^2\rp\rp =-\dfrac16+o(1)$

ce qui montre la limite

$\lim_{x\to0}(x)=-\dfrac16$

Tag:DL

Autres sujets au hasard:

Voir aussi: