Tangente commune à deux courbes
Exercice corrigé - Spécialité maths, première générale
Énoncé
Soit 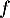 la fonction définie sur
la fonction définie sur 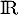 par l'expression
par l'expression 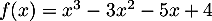 .
.
On note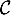 sa courbe représentative dans un repère orthonormal
sa courbe représentative dans un repère orthonormal 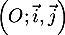 .
.
On note
- Etudier la fonction
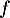 , et tracer la courbe
, et tracer la courbe 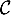 .
.
- Soit
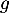 la fonction définie par l'expression
la fonction définie par l'expression
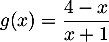 .
On note
.
On note 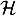 sa courbe représentative dans le même repère.
sa courbe représentative dans le même repère.
Etudier la fonction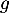 et tracer
et tracer 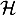 .
.
- Vérifier que les courbes
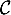 et
et 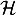 passent par le même point
passent par le même point 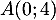 .
Déterminer alors les coordonnées de tous les points d'intersection
de
.
Déterminer alors les coordonnées de tous les points d'intersection
de 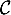 et
et 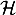 .
.
- Démontrer que les deux courbes ont une tangente commune en
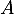 .
.
Correction
Correction
- La fonction
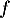 est une fonction polynôme du troisième
degré, et est donc définie et dérivable sur
est une fonction polynôme du troisième
degré, et est donc définie et dérivable sur 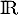 ,
avec,
pour tout
,
avec,
pour tout 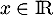 ,
, 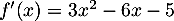 .
Le discriminant de
.
Le discriminant de 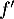 est
est 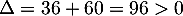 , et donc
, et donc 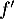 admet
deux racines:
admet
deux racines:
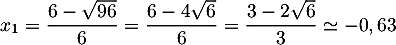 et
et
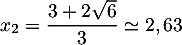 .
.
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $x_1$ && $x_2$ && $+\infty$ \\\hline
$f'(x)$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} &$-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ &\\\hline
&&&$\simeq5,70$&&&&\\
$f$ && \Large{$\nearrow$} && \Large{$\searrow$} &&
\Large{$\nearrow$} & \\
&&&&&$\simeq -11,71$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/extgcom_c/10.png)
- La fonction
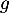 est le quotient des fonctions
est le quotient des fonctions 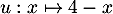 et
et 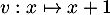 qui sont dérivables sur
qui sont dérivables sur 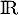 , avec
, avec
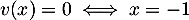 .
.
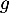 est donc définie et dérivable sur
est donc définie et dérivable sur 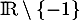 ,
et, pour tout
,
et, pour tout 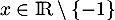 ,
,
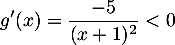 :
: 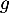 est strictement décroissante
sur
est strictement décroissante
sur ![$]-\infty;-1[$](/Generateur-Devoirs/1S/Chap3/extgcom_c/21.png) et sur
et sur ![$]-1;+\infty[$](/Generateur-Devoirs/1S/Chap3/extgcom_c/22.png) .
.
![\[\psset{xunit=1cm,yunit=0.2cm}
\begin{pspicture}(-6,-20)(5,20)
\psline[linewidth=0.8pt]{->}(-3,0)(4.5,0)
\psline[linewidth=0.8pt]{->}(0,-20)(0,20)
\psline[linewidth=1.4pt]{->}(0,0)(1,0)
\psline[linewidth=1.4pt]{->}(0,0)(0,1)
\psplot[linewidth=1pt]{-2.3}{4.5}{
x x mul x mul
-3 x mul x mul add
-5 x mul add
4 add
}
\psline{<->}(-2,5.70)(0.5,5.70)
\psline{<->}(1,-11.71)(4,-11.71)
\rput(4.8,12){$\mathcal{C}$}
\psplot[linewidth=1pt]{-3}{-1.25}{
4 x sub
x 1 add div
}
\psplot[linewidth=1pt]{-0.75}{4}{
4 x sub
x 1 add div
}
\psline[linewidth=0.5pt](-1,-20)(-1,20)
\rput(-3,-2){$\mathcal{H}$}
\rput(-.5,18){$\mathcal{H}$}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap3/extgcom_c/23.png)
- On a
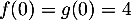 , et donc le point
, et donc le point 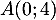 est un point de
est un point de
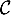 et de
et de 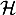 .
.
Les points d'intersection de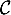 et
et 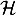 ont
pour abscisse
ont
pour abscisse 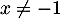 tel que
tel que 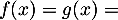 , soit
, soit
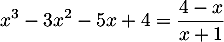 ,
,
soit aussi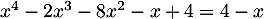 ,
,
soit donc,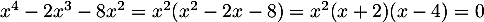 ,
d'où
,
d'où  ou
ou  ou
ou 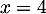 .
Les points d'intersection sont donc
.
Les points d'intersection sont donc
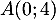 ,
,  et
et  .
.
- La tangente à
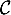 en
en 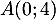 a pour équation
a pour équation
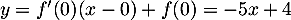 .
.
La tangente à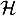 en
en 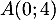 a pour équation
a pour équation
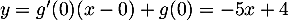 .
.
Les courbes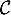 et
et 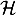 ont donc la droite
d'équation
ont donc la droite
d'équation 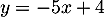 comme tangente commune en
comme tangente commune en 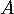 .
.
On dit que les courbes et
et  sont
tangentes en
sont
tangentes en  .
.
Tag:Fonctions et dérivées
Voir aussi:
Quelques devoirs
second degré (équation et inéquation, tableau de signe). Dérivabilité d'une fonction en un point: taux d'accroissement et nombre dérivé (calcul et lecture graphique)
fonctions dérivées, étude de fonction et position relative de deux courbes
dérivées et étude de fonction. Angles en radians sur le cercle trigonométrique et en mesure principale
second degré, factorisation d'un polynome du 3ème degré. Calculs de fonctions dérivées et équation d'une tangente
Mesure principale d'un angle en radians - Etude des variations d'une fonctions - Etude d'une fonction auxilaire et TVI
