Vrai ou faux
Exercice corrigé - Spécialité maths, première générale
Énoncé
Vrai ou Faux ?
Pour chacune des propositions suivantes, dire si elle est vraie ou fausse. Justifier. (On pourra par exemple, dans certains cas, donner un exemple ou un contre exemple).
Pour chacune des propositions suivantes, dire si elle est vraie ou fausse. Justifier. (On pourra par exemple, dans certains cas, donner un exemple ou un contre exemple).
- Il existe des fonctions dérivables et monotones sur
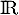 qui n'ont pas de maximum sur
qui n'ont pas de maximum sur 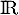 .
.
- Soit
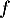 une fonction dérivable sur un intervalle
une fonction dérivable sur un intervalle 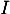 et positive sur
et positive sur 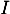 .
.
Alors, les fonctions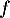 et
et 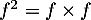 ont le même sens de variation sur
ont le même sens de variation sur 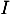 .
.
- Soit
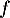 une fonction définie sur
une fonction définie sur ![$[a;b]$](/Generateur-Devoirs/1S/Chap3/exVF/10.png) .
Si l'équation
.
Si l'équation 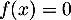 admet une solution unique, alors
admet une solution unique, alors 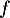 est strictement monotone sur
est strictement monotone sur ![$[a;b]$](/Generateur-Devoirs/1S/Chap3/exVF/13.png) .
.
- La fonction
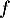 définie par
définie par 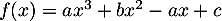 ,
, 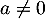 , n'admet aucun extremum.
, n'admet aucun extremum.
Correction
Correction
Vrai ou Faux ?- Vrai. Par exemple la fonction
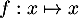 (ou même
plus généralement toute fonction affine), est dérivable sur
(ou même
plus généralement toute fonction affine), est dérivable sur 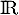 ,
strictement croissante, et n'admet pas de maximum.
,
strictement croissante, et n'admet pas de maximum.
- Vrai.
Comme
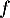 est dérivable sur
est dérivable sur 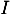 ,
, 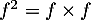 l'est aussi,
et, pour tout
l'est aussi,
et, pour tout 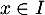 ,
,
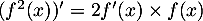 .
.
Comme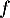 est positive sur
est positive sur 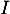 , c'est-à-dire pour tout
, c'est-à-dire pour tout
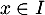 ,
, 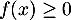 , la dérivée de
, la dérivée de 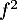 et
et 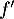 ont le même
signe, ce qui montre que
ont le même
signe, ce qui montre que 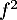 et
et 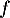 ont le même sens de
variation.
ont le même sens de
variation.
- Faux. La propriété ``
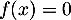 '' indique
géométriquement que la courbe représentative de la fonction
'' indique
géométriquement que la courbe représentative de la fonction 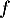 coupe l'axe des abscisses une unique fois, et c'est tout! en
particulier cette propriété ne donne aucune information sur le
comportement de la courbe de part et d'autre de cette intersection.
coupe l'axe des abscisses une unique fois, et c'est tout! en
particulier cette propriété ne donne aucune information sur le
comportement de la courbe de part et d'autre de cette intersection.
Par exemple, la fonction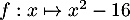 définie sur
définie sur ![$[-10;3]$](/Generateur-Devoirs/1S/Chap3/exVF_c/19.png) ,
vérifie cette propriété, la seule racine étant
,
vérifie cette propriété, la seule racine étant 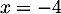 dans cet
intervalle, et est pourtant décroissante sur
dans cet
intervalle, et est pourtant décroissante sur ![$[-10;-4]$](/Generateur-Devoirs/1S/Chap3/exVF_c/21.png) et
croissante sur
et
croissante sur ![$[-4;3]$](/Generateur-Devoirs/1S/Chap3/exVF_c/22.png) .
.
- Faux.
La fonction
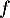 est une fonction polynôme, donc dérivable
sur
est une fonction polynôme, donc dérivable
sur 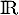 , avec, pour tout
, avec, pour tout 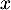 réel:
réel:
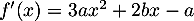 .
.
Le discriminant de ce trinôme est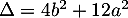 .
.
 est une somme de nombres positifs et donc
est une somme de nombres positifs et donc 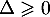 .
.
De plus, comme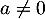 , on a
, on a 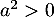 et donc aussi
et donc aussi 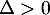 .
Ainsi, ce trinôme
.
Ainsi, ce trinôme 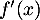 change de signe sur
change de signe sur 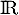 , et donc la fonction
, et donc la fonction 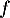 change de sens de variation deux fois sur
change de sens de variation deux fois sur 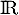 .
Elle admet donc deux extrema, un maximum et un minimum.
.
Elle admet donc deux extrema, un maximum et un minimum.
Tag:Fonctions et dérivées
Voir aussi:
Quelques devoirs
second degré (équation et inéquation, tableau de signe). Dérivabilité d'une fonction en un point: taux d'accroissement et nombre dérivé (calcul et lecture graphique)
fonctions dérivées, étude de fonction et position relative de deux courbes
dérivées et étude de fonction. Angles en radians sur le cercle trigonométrique et en mesure principale
second degré, factorisation d'un polynome du 3ème degré. Calculs de fonctions dérivées et équation d'une tangente
Mesure principale d'un angle en radians - Etude des variations d'une fonctions - Etude d'une fonction auxilaire et TVI
