Fonction avec 4 paramètres à trouver
Exercice corrigé - Spécialité maths, première générale
Énoncé
La courbe 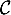 suivante représente une fonction
suivante représente une fonction 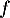 définie sur
définie sur 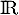 et dont l'expression est de la forme
et dont l'expression est de la forme
![\[f(x)=ax^3+bx^2+cx+d\]](/Generateur-Devoirs/1S/Chap3/exparam/4.png)
où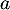 ,
, 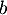 ,
, 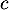 et
et 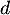 sont quatre réels.
sont quatre réels.
La tangente à
à 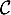 à l'origine
à l'origine  passe par le point
passe par le point 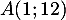 , et la tangente au point
, et la tangente au point 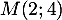 de
de 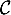 est horizontale.
est horizontale.
![\[\psset{xunit=1.5cm,yunit=0.3cm}
\begin{pspicture}(-1,-4.6)(3.5,13.)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(-1.5,0)(3.5,0)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,-5.5)(0,13.2)
%\rput(-0.2,0.5){$O$}
%
\multido{\i=-1+1}{5}{
\psline[linestyle=dashed,linewidth=0.3pt](\i,-5)(\i,12.8)
\rput(\i,-0.5){$\i$}
}
\multido{\i=-4+2}{9}{
\psline[linestyle=dashed,linewidth=0.3pt](-1.2,\i)(3.2,\i)
\rput(-0.2,\i){$\i$}
}
%
\psplot[linewidth=1.5pt]{-0.4}{3.2}{2 x 3 exp mul -9 x 2 exp mul add 12 x mul add}
\rput(2.8,9){\large$\Cf$}
\rput(2,4){$\tm$}
\rput(1.8,3.5){$M$}
%
\psplot{-0.5}{1.1}{12 x mul}
\rput(0.6,9){$T$}
\rput(1,12){$\tm$}\rput(0.8,12.45){\large$A$}
\end{pspicture}
\]](/Generateur-Devoirs/1S/Chap3/exparam/15.png)
où
La tangente
![\[\psset{xunit=1.5cm,yunit=0.3cm}
\begin{pspicture}(-1,-4.6)(3.5,13.)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(-1.5,0)(3.5,0)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,-5.5)(0,13.2)
%\rput(-0.2,0.5){$O$}
%
\multido{\i=-1+1}{5}{
\psline[linestyle=dashed,linewidth=0.3pt](\i,-5)(\i,12.8)
\rput(\i,-0.5){$\i$}
}
\multido{\i=-4+2}{9}{
\psline[linestyle=dashed,linewidth=0.3pt](-1.2,\i)(3.2,\i)
\rput(-0.2,\i){$\i$}
}
%
\psplot[linewidth=1.5pt]{-0.4}{3.2}{2 x 3 exp mul -9 x 2 exp mul add 12 x mul add}
\rput(2.8,9){\large$\Cf$}
\rput(2,4){$\tm$}
\rput(1.8,3.5){$M$}
%
\psplot{-0.5}{1.1}{12 x mul}
\rput(0.6,9){$T$}
\rput(1,12){$\tm$}\rput(0.8,12.45){\large$A$}
\end{pspicture}
\]](/Generateur-Devoirs/1S/Chap3/exparam/15.png)
- Déterminer les réels
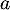 ,
, 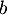 ,
, 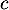 et
et 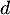 .
.
- Il semblerait que
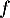 admette un maximum local en
admette un maximum local en  .
Est-ce vraiment le cas ?
Quelle est la valeur de ce maximum ?
.
Est-ce vraiment le cas ?
Quelle est la valeur de ce maximum ?
- Montrer que la courbe
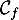 ne coupe l'axe des abscisses qu'en
l'origine.
ne coupe l'axe des abscisses qu'en
l'origine.
- En quels points
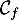 admet-elle une tangente parallèle à
admet-elle une tangente parallèle à 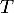 ?
?
Correction
Correction
- On sait que
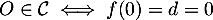 .
.
La tangente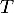 en
en  à
à 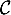 passe par les points
passe par les points 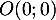 et
et
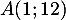 et a donc pour coefficient directeur
et a donc pour coefficient directeur
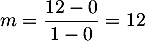 .
Ainsi,
.
Ainsi, 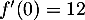 .
Or, pour tout réel
.
Or, pour tout réel 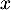 ,
, 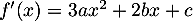 ,
et donc,
,
et donc, 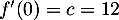 .
.
On a de même, en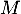 ,
,
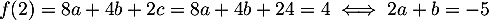 ,
et,
,
et, 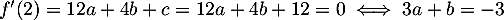
En soustrayant ces deux dernières équations, on obtient , et donc,
, et donc, 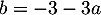 soit
soit 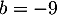 .
.
Ainsi, pour tout réel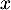 ,
,
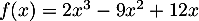 .
.
- Pour tout réel
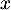 ,
,
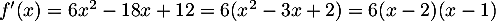 (car on a déterminé
(car on a déterminé 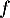 au 1. justement pour que
au 1. justement pour que 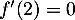 ,
c'est-à-dire que
,
c'est-à-dire que 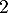 soit une racine de
soit une racine de 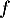 ).
).
On a alors le tableau de variation suivant, qui montre que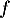 admet bien un maximum local en
admet bien un maximum local en  , et
qui vaut
, et
qui vaut 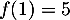 .
.
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $1$ && $2$ && $+\infty$ \\\hline
$f'(x)$ && $+$ &\zb&$-$&\zb&$+$& \\\hline
&&&5&&&&\\
$f(x)$&& \psline{->}(-0.5,-0.4)(0.5,0.5)&&
\psline{->}(-0.5,0.5)(0.5,-0.4)&&
\psline{->}(-0.5,-0.4)(0.5,0.5)&\\
&&&&&4&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exparam_c/29.png)
- On peut raisonner de (au moins) deux manières:
-
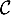 coupe l'axe des abscisses aux points
coupe l'axe des abscisses aux points 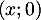 tels que
tels que
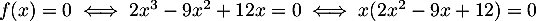 , ainsi, soit
, ainsi, soit 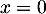 (origine du repère),
soit
(origine du repère),
soit 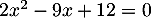 .
.
Ce trinôme a pour discriminant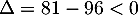 et n'admet donc
pas de racine réelle.
et n'admet donc
pas de racine réelle.
Ainsi,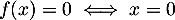 ,
et
,
et  coupe l'axe des abscisses uniquement à l'origine.
coupe l'axe des abscisses uniquement à l'origine.
- D'après le tableau de variation de
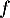 ,
sur
,
sur ![$]-\infty;1]$](/Generateur-Devoirs/1S/Chap3/exparam_c/39.png) ,
,  est strictement croissante et
est strictement croissante et 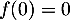 est
donc l'unique solution de l'équation
est
donc l'unique solution de l'équation 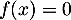 sur
sur ![$]-\infty;1]$](/Generateur-Devoirs/1S/Chap3/exparam_c/43.png) ,
d'après le théorème des valeurs intermédiaires.
,
d'après le théorème des valeurs intermédiaires.
Sur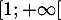 ,
, 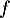 a pour minimum global
a pour minimum global 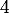 , et donc,
pour tout
, et donc,
pour tout 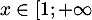 ,
, 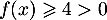 ,
et l'équation
,
et l'équation 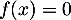 ne peut donc pas avoir de solution.
ne peut donc pas avoir de solution.
En résumé, l'équation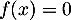 admet pour unique solution sur
admet pour unique solution sur 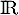
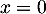 , et
, et 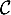 coupe l'axe des abscisses uniquement en
l'origine.
coupe l'axe des abscisses uniquement en
l'origine.
-
- La droite
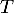 a pour coefficient directeur
a pour coefficient directeur 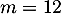 .
.
Une tangente à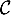 au point d'abscisse
au point d'abscisse 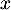 est donc parallèle à
est donc parallèle à
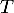 si et seulement si
si et seulement si
 .
.
On a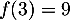 , et donc
, et donc  admet une seule autre tangente
parallèle à
admet une seule autre tangente
parallèle à  , sa tangente au point
, sa tangente au point 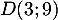 .
.
Tag:Fonctions et dérivées
Voir aussi:
Quelques devoirs
second degré (équation et inéquation, tableau de signe). Dérivabilité d'une fonction en un point: taux d'accroissement et nombre dérivé (calcul et lecture graphique)
fonctions dérivées, étude de fonction et position relative de deux courbes
dérivées et étude de fonction. Angles en radians sur le cercle trigonométrique et en mesure principale
second degré, factorisation d'un polynome du 3ème degré. Calculs de fonctions dérivées et équation d'une tangente
Mesure principale d'un angle en radians - Etude des variations d'une fonctions - Etude d'une fonction auxilaire et TVI
