Pour un premier devoir...
Exercice corrigé - Spécialité maths, première générale
Énoncé
- Ecrire le polynôme
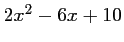 sous forme canonique.
sous forme canonique.
- Résoudre les équations suivantes :
- On cherche à résoudre l'équation
 .
.
- Montrer que

- Résoudre alors l'équation
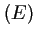 .
.
- Montrer que
Correction
Correction
-
![$ 2x^2-6x+10=2(x^2-3x+5)
=2\left[\left(x-\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2+5\right]
=2\left[\left(x-\frac{3}{2}\right)^2+\frac{11}{4}\right]$](/Generateur-Devoirs/1S/Chap1/ex8_c_img1.png) .
.
-
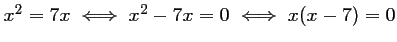 soit
soit 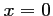 ou
ou 
-
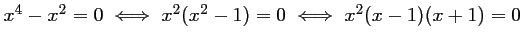 soit
soit 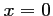 ou
ou 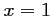 ou
ou 
-

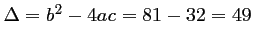 :
:  donc l'équation admet deux racines réelles distinctes :
donc l'équation admet deux racines réelles distinctes :
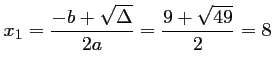 et
et 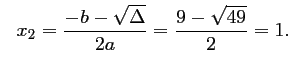
-
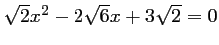
 :
:
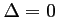 donc l'équation admet une racine réelle double :
donc l'équation admet une racine réelle double :
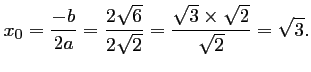
-
-
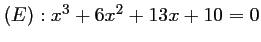 .
.
-
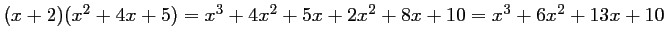
-

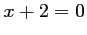 soit
soit
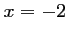 ou
ou
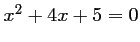 :
:
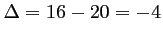 :
:
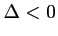 donc l'équation du second degré n'admet pas de racine réelle.
donc l'équation du second degré n'admet pas de racine réelle.
Finalement, l'équation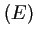 admet pour unique solution
admet pour unique solution 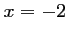 .
.
-
Tag:2nd degré
Voir aussi:
Quelques devoirs
équations et inéquations du second degré. Racines d'une fonction trinôme du 2nd degré. Polynome du 3ème degré: factorisation et signe d'une fractoion rationnelle
second degré (équation et inéquation, tableau de signe). Dérivabilité d'une fonction en un point: taux d'accroissement et nombre dérivé (calcul et lecture graphique)
équations et inéquations du second degré. Racines d'une fonction trinôme du 2nd degré
second degré, factorisation d'un polynome du 3ème degré. Équation (réduite) de droite
second degré, factorisation d'un polynome du 3ème degré. Équation (réduite) de droite
