Matrices qui commutent

Exercice corrigé - Maths expertes, terminale générale

Énoncé

$A$ et $B$ sont deux matrices carrées d'ordre $n$ telles que $AB = A + I_n$.
On suppose que $A$ est inversible et que $A^{-1} = B-I_n$, démontrer alors que $A$ et $B$ commutent, c'est-à-dire que $AB = BA$


Correction

Correction

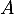En utilisant la définition de la matrice inverse $A$ et la matrice inverse 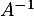$A^{-1}$ donnée, on a
\[A^{-1}A=(B-I_n)A=BA-A=I_n\]

et on trouve donc que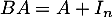 $BA=A+I_n$ qui est aussi exactement l'epxression du produit $AB$.
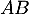On a donc ainsi bien trouvé que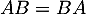 $AB=BA$, c'est-à-dire que ces matrices commutent.


Tag:matrices

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs


LongPage: h2: 3 - h3: 0