Devoir de maths corrigé, Plan complexe
Maths expertes, terminale générale
Devoir de mathématiques, et corrigé, sur les nombres complexes posé en maths expertes, terminale générale, année scolaire 2024/2025
Exercice 1: Lieux de points dans le plan complexe, et équation cartésienne
Représenter graphiquement et donner l'équation cartésienne, de l'ensemble des points 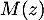 tels que
tels que
a)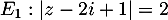 ,
b)
,
b) 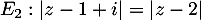
Cacher la correction
a)
Correction exercice 1
- Soit
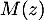 et
et 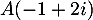 alors on a
alors on a
![\[\begin{array}{rl}
M\in E_1 \iff&|z-2i+1|=2\\[.5em]
\iff&|z-(-1+2i)|=2\\[.5em]
\iff&AM=2\enar\]](/Generateur-Devoirs/Mex/CplxPlan/exlieux0_c/3.png)
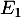 est donc le cercle de entre
est donc le cercle de entre 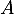 et de rayon 2.
et de rayon 2.
{$A$}
\psline[linestyle=dashed](-1,0)(-1,2)(0,2)
\rput[l](.2,2){$2$}\rput(-1,-.4){$-1$}
\psarc[linewidth=1.3pt,linecolor=red](-1,2){2}{0}{360}
\psline[linewidth=1.5pt]{->}(0,0)(1,0)
\psline[linewidth=1.5pt]{->}(0,0)(0,1)
\rput(-.2,-.2){$O$}
\rput(-.3,.3){$\vec{v}$}
\rput(.3,-.3){$\vec{u}$}
\end{pspicture*}\]](/Generateur-Devoirs/Mex/CplxPlan/exlieux0_c/6.png)
Pour obtenir l'équation cartésienne, on introduit les coordonnées cartésiennes des points: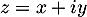 et
et 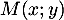 et
et 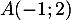 et alors, en élevant au carré,
et alors, en élevant au carré,
![\[\begin{array}{ll}|z-2i+1|^2&=|(x+1)+i(y-2)|^2\\[.5em]
&=(x+1)^2+(y-2)^2\enar\]](/Generateur-Devoirs/Mex/CplxPlan/exlieux0_c/10.png)
d'où l'équation cartésienne du cercle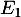 :
:
![\[(x+1)^2+(y-2)^2=4\]](/Generateur-Devoirs/Mex/CplxPlan/exlieux0_c/12.png)
- Soit
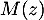 et
et 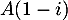 et
et 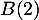 alors on a
alors on a
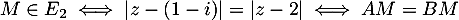 .
.
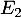 est donc la médiatrice du segment
est donc la médiatrice du segment ![$[AB]$](/Generateur-Devoirs/Mex/CplxPlan/exlieux0_c/18.png) .
.
{$A$}
\rput(2,0){$\tm$}\rput(2.2,.2){$B$}
\psline[linewidth=1.5pt]{->}(0,0)(1,0)
\psline[linewidth=1.5pt]{->}(0,0)(0,1)
\rput(-.2,-.2){$O$}
\rput(-.3,.3){$\vec{v}$}
\rput(.3,-.3){$\vec{u}$}
\psline(1,-1)(2,0)
% V{AB}(1,1) I(1.5,-.5)
%\overrightarrow{IM}.\overrightarrow{AB}=0 \iff (x-1.5)+(y+0.5)=0 \iff y=-x+1
\psplot[linewidth=1.3pt,linecolor=red]{-3}{3}{-1 x mul 1 add}
\rput(-1,2.6){\red$E_2$}
\end{pspicture*}\]](/Generateur-Devoirs/Mex/CplxPlan/exlieux0_c/19.png)
Pour obtenir l'équation cartésienne de la droite, on pose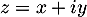 et alors, en élevant aux carré les modules qui sont des nombres positifs
et alors, en élevant aux carré les modules qui sont des nombres positifs
![\[\begin{array}{rl}(E_2):&|z-1+i|=|z-2|\\[.5em]
\iff&|(x-1)+i(y+1)|^2=|(x-2)+iy|^2\\[.5em]
\iff&(x-1)^2+(y+1)^2=(x-2)^2+y^2
\enar\]](/Generateur-Devoirs/Mex/CplxPlan/exlieux0_c/21.png)
En développant les identités remarquables, tous les carrés se simplifient et il reste alors
![\[\begin{array}{rl}(E_2): &x^2-2x+1+y^2+2y+1=x^2-4x+4+y^2\\[.5em]
\iff&2x+2y-2=0\enar\]](/Generateur-Devoirs/Mex/CplxPlan/exlieux0_c/22.png)
ou encore l'équation cartésienne de la droite: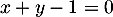 ou aussi l'équation réduite
ou aussi l'équation réduite 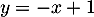
Cacher la correction
Exercice 2: Formes algébrique, trigonométrique et exponentielle de nombres complexes
(Baccalauréat France métropolitaine, Septembre 2007, 5 points)
Soit les nombres complexes :
![\[z_{1} = \sqrt{2} + \text{i}\sqrt{6},~ z_{2} = 2 + 2\text{i}\quad \text{et} \quad Z = \dfrac{z_{1}}{z_{2}}.\]](/Generateur-Devoirs/Mex/CplxPlan/expi12/1.png)
Cacher la correction
- Écrire
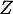 sous forme algébrique.
sous forme algébrique.
- Donner les modules et arguments de
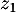 ,
, 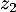 et
et 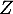 .
.
- En déduire
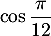 et
et 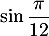 .
.
- Écrire sous forme algébrique le nombre complexe
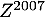 .
.
Correction exercice 2
- On a
![\[\begin{array}{ll}Z&= \dfrac{z_1}{z_2} = \dfrac{\sqrt2 + i\sqrt6}{2 + 2i}\\[.8em]
&=\dfrac{(\sqrt2 + i\sqrt6)(2-2i)}{(2 + 2i)(2-2i)}\\[.8em]
&=\dfrac{2\sqrt2+2\sqrt6-2i\sqrt2+2i\sqrt6}{8}\\[.8em]
&=\dfrac14\lp\sqrt2+\sqrt6\rp+\dfrac14i\lp-\sqrt2+\sqrt6\rp\enar\]](/Generateur-Devoirs/Mex/CplxPlan/expi12_c/1.png)
-
-
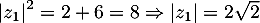 . On a donc
. On a donc 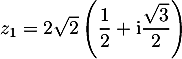 . Donc arg
. Donc arg![$(z_{1}) = \dfrac{\pi}{3}~~[2\pi]$](/Generateur-Devoirs/Mex/CplxPlan/expi12_c/4.png) .
.
- On a de même
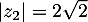 , puis
, puis 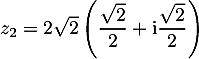 .
Donc arg
.
Donc arg![$(z_{2}) = \dfrac{\pi}{4}~~[2\pi]$](/Generateur-Devoirs/Mex/CplxPlan/expi12_c/7.png) .
.
- Il suit alors
![\[\begin{array}{ll}\text{arg}(Z)&=\arg\lp\dfrac{z_1}{z_2}\rp\\[.8em]
&=\arg(z_1)-\arg(z_2)\\[.6em]
&=\dfrac\pi3-\dfrac\pi4
=\dfrac{\pi}{12}~[2\pi]
\enar\]](/Generateur-Devoirs/Mex/CplxPlan/expi12_c/8.png)
On calcule aussi le module:
![\[|Z| = \dfrac{|z_1|}{|z_2|}=1\]](/Generateur-Devoirs/Mex/CplxPlan/expi12_c/9.png)
-
- On déduit des cacluls précédents que
![\[Z = \cos \left( \dfrac{\pi}{12}\right) + i\sin \left(\dfrac{\pi}{12}\right)\]](/Generateur-Devoirs/Mex/CplxPlan/expi12_c/10.png)
et alors par identification avec la forme algébrique de la question 1):
![\[\la\begin{array}{ll}
\cos \lp\dfrac{\pi}{12}\right) &= \dfrac14\lp\sqrt2+\sqrt6\right)\\[.8em]
\sin \lp\dfrac{\pi}{12}\right) &= \dfrac14\lp-\sqrt2+\sqrt6\right)
\enar\right.\]](/Generateur-Devoirs/Mex/CplxPlan/expi12_c/11.png)
- On calcule le module:
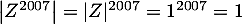
puis l'argument:
![\[\begin{array}{ll}\text{arg}\left( Z^{2007} \right) &= 2007\times \dfrac{\pi}{12}= \dfrac{669\pi}{4}\\[.8em]
&= 168\pi - \dfrac{3\pi}{4} \equiv -\dfrac{3\pi}{4}~[2\pi]\enar\]](/Generateur-Devoirs/Mex/CplxPlan/expi12_c/13.png)
On a donc
![\[\begin{array}{ll}Z^{2007} = e^{-\frac{3\pi}{4}}
&= \cos\lp-\frac{3\pi}{4} \right) + i\sin\lp-\frac{3\pi}{4}\right)\\[.8em]
&= - \dfrac{\sqrt2}{2} - i\dfrac{\sqrt2}{2}\enar\]](/Generateur-Devoirs/Mex/CplxPlan/expi12_c/14.png)
Cacher la correction
Exercice 3: Racines d'une équation du 2nd degré sous forme exponentielle
Résoudre dans 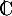 l'équation
l'équation 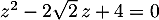 .
.
Écrire les solutions sous forme exponentielle.
Le discriminant de cette équation du second degré est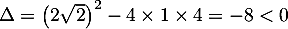 .
.
L'équation admet donc deuxsolutions complexes conjuguées:
![\[z_1=\dfrac{2\sqrt2-i\sqrt{8}}{2}=\dfrac{2\sqrt2-i2\sqrt2}{2}=\sqrt2\lp1-i\rp\]](/Generateur-Devoirs/Mex/CplxPlan/ex2ndexp_c/2.png)
et
![\[z_2=\overline{z_1}=\sqrt2\lp1+i\rp\]](/Generateur-Devoirs/Mex/CplxPlan/ex2ndexp_c/3.png)
Pour écrire sous forme exponentielle ces racines, on détermine leur module et leur argument.
On a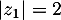 et
et 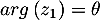 tel que
tel que
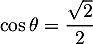 et
et 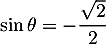 .
.
On trouve ainsi que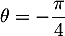 , et donc la forme exponentielle
, et donc la forme exponentielle
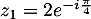 .
.
On a alors pour la deuième racine
![\[z_2=\overline{z_1}=2e^{i\frac{\pi}{4}}\]](/Generateur-Devoirs/Mex/CplxPlan/ex2ndexp_c/10.png)
Cacher la correction
Écrire les solutions sous forme exponentielle.
Correction exercice 3
Le discriminant de cette équation du second degré est
L'équation admet donc deuxsolutions complexes conjuguées:
et
Pour écrire sous forme exponentielle ces racines, on détermine leur module et leur argument.
On a
On trouve ainsi que
On a alors pour la deuième racine
Cacher la correction
Quelques autres devoirs
sur la division euclidienne et les congruences. Nombres complexes: calcul algébrique, inverse et module. Résolution d'une équation.
sur le plan complexe: ensemble de points dans le plan complexe, forme exponentielle et équation du second degré complexe
sur le plan complexe, les nombres complexes en géométrie, et les congruences en arithmétiques. Ecritures algébriques, trigonométrique et exponentielle d'un nombre complexe. Application au calcul de la puissance d'un nombre complexe. Calcul des valeurs exactes des cosinus et sinus de π/12. Congruences et chiffre des unités d'une puissance
sur le plan complexe, les nombres complexes en géométrie, et les congruences en arithmétiques. Ecritures algébriques, trigonométrique et exponentielle d'un nombre complexe. Application au calcul de la puissance d'un nombre complexe. Critère de divisibilité par 19
sur les matrices, calcul matriciel et les nombres complexes: géométrie, formes algébriques et exponentielles.
Quelques exercices corrigés
Exercices corrigés
Calculs algébriques, modules et une équation
Exercices corrigés
Ensembles de points du plan complexe, modules et équations cartésiennes
Exercices corrigés
Ensembles de points du plan complexe
Exercices corrigés
Formes algébriques et exponentielles et valeur exacte cosinus
Exercices corrigés
Formes algébriques et exponentielles et cosinus pi sur 12
Voir aussi: