Calculs algébriques, modules et une équation
Exercice corrigé - Maths expertes, terminale générale
Énoncé
- Soit
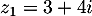 .
.
Écrire sous forme algébrique le nombre complexe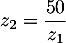 .
.
Calculer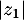 et
et 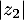 .
.
- Déterminer l'ensemble des nombres complexes
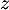 tels que
tels que 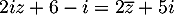
Correction
Correction
-
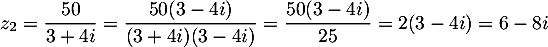
On calcule alors les modules: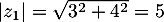 et
et 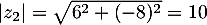
- Soit
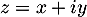 , avec
, avec 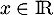 et
et 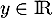 tel que
tel que
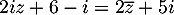 alors
alors
![\[\begin{array}{ll}&2i(x+iy)+6-i=2(x-iy)+5i\\
\iff&(-2y+6)+i(2x-1)=2x+i(-2y+5)
\enar\]](/Generateur-Devoirs/Mex/CplxPlan/ex0_c/8.png)
On identifie alors les parties réelles et imaginaires:
![\[\la\begin{array}{rcl}
-2y+6&=&2\\
2x-1&=&-2y+5\enar\right.\]](/Generateur-Devoirs/Mex/CplxPlan/ex0_c/9.png)
La première équation donne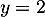 et la deuxième devient alors
et la deuxième devient alors
![\[2x-1=-4+5=1\iff x=1\]](/Generateur-Devoirs/Mex/CplxPlan/ex0_c/11.png)
La solution est alors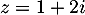
Tags:Nombres Complexes - AlgébriquePlan complexe
Voir aussi:
Quelques devoirs
sur les nombres complexes: forme algébrique des nombres complexes et résolution d'équations complexes
sur les nombres complexes: résolution d'équations et forme algébrique. Arithmétique, divisibilité et division euclidienne
sur les nombres complexes, point de vue algébrique. Calculs algébriques sur les nombres complexes, inverse d'un nombre complexe et résolution d'équations
sur les nombres complexes et polynômes. Résolution d'une éuqation complexe. Racine d'un polynôme et factorisation du polynôme. Quotients et restes de division euclidienne. Divisiblité par 8
