Puissance n-ième d'une matrice, par récurrence, et limites suites récurrentes imbriquées
Exercice corrigé - Maths expertes, terminale générale
Énoncé
On considère la matrice carrée 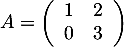 .
.
- Calculer
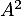 .
.
- Montrer que, pour tout entier naturel
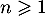 , on a
, on a
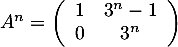 .
.
- Déterminer les limites des suites
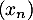 et
et 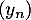 définies, pour tout entier
définies, pour tout entier 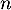 , par
, par
![\[
x_0=1\ ;\ y_0=-5 \quad\text{ et, }\quad
\la\begin{array}{ll}x_{n+1}=x_n+2y_n\\y_{n+1}=3y_n\enar\right.
\]](/Generateur-Devoirs/Mex/Matrices/exsulim/8.png)
Correction
Correction
-
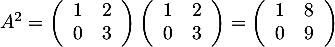
- On peut démontrer cette propriété par récurrence.
Initialisation. Pour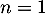 , on a
, on a
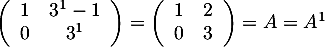 ,
est la propriété est donc initialement vraie au rang
,
est la propriété est donc initialement vraie au rang  .
.
Hérédité. Supposons que pour un entier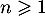 on ait
on ait
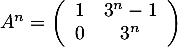 .
.
Alors, au rang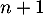 ,
,
![\[\begin{array}{ll}A^{n+1}&=A^n\,A
=\lp\begin{array}{cc}1&3^n-1\\0&3^n\enar\rp\lp\begin{array}{cc}1&2\\0&3\enar\rp\\[.6cm]
&=\lp\begin{array}{cc}1&1\tm2+\lp3^n-1\rp\tm3\\0&3^n\tm3\enar\rp\\[.6cm]
&=\lp\begin{array}{cc}1&2+3^{n+1}-3\\0&3^{n+1}\enar\right)
=\lp\begin{array}{cc}1&3^{n+1}-1\\0&3^{n+1}\enar\right)
\enar\]](/Generateur-Devoirs/Mex/Matrices/exsulim_c/8.png)
ce qui montre que la propriété est encore vraie au rang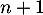 .
.
Conclusion. On vient donc de démontrer, d'après le principe de récurrence, que pour tout entier naturel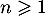 ,
,
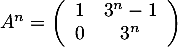 .
.
- Sous forme matricielle, en introduisant la suite
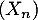 définie pour tout entier naturel
définie pour tout entier naturel 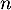 par
par
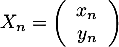 , on a
, on a
![\[\la\begin{array}{ll}x_{n+1}=x_n+2y_n\\y_{n+1}=3y_n\enar\right.
\iff X_{n+1}=AX_n \]](/Generateur-Devoirs/Mex/Matrices/exsulim_c/15.png)
Ainsi,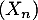 est une suite géométrique, et donc, pour tout
entier
est une suite géométrique, et donc, pour tout
entier 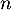 ,
,
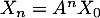 avec
avec 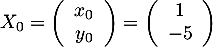 .
.
D'après le résultat de la question précédente, on a donc
![\[X_n=\lp\begin{array}{c}x_n\\y_n\enar\right)
=\lp\begin{array}{cc}1&3^n-1\\0&3^n\enar\right) \lp\begin{array}{c}1\\-5\enar\right)
=\lp\begin{array}{cc}1-5\lp3^n-1\rp\\-5\tm3^n\enar\rp
\]](/Generateur-Devoirs/Mex/Matrices/exsulim_c/20.png)
soit
![\[\la\begin{array}{ll}
x_n&=1-5(3^n-1)=-5\tm3^n+6\\[.3cm]
y_n&=-5\tm3^n
\enar\right.\]](/Generateur-Devoirs/Mex/Matrices/exsulim_c/21.png)
Comme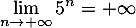 , on a alors
, on a alors
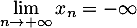 et de même
et de même
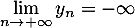
Tag:matrices
Voir aussi:
Quelques devoirs
sur les matrices et calcul matriciel, produit, puissance d'une matrice, définition de l'inverse d'une matrice
sur la factorisation et racines d'un polynôme complexe et matrices et calcul matriciel, diagonalisation et limites de suites
sur binôme de Newton et les racines de l'unité. Calcul de la puissance n-ième d'une matrice
sur les matrices, calcul matriciel et les nombres complexes: géométrie, formes algébriques et exponentielles.
