Matrice nilpotente et inverse
Exercice corrigé - Maths expertes, terminale générale
Énoncé
Soit 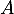 une matrice nilpotente, c'est-à-dire telle qu'il existe un entier
une matrice nilpotente, c'est-à-dire telle qu'il existe un entier 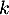 tel que
tel que 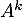 est la matrice nulle.
est la matrice nulle.
Montrer que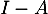 est inversible et que son inverse s'écrit sous la forme
est inversible et que son inverse s'écrit sous la forme 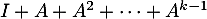 .
.
En déduire l'inverse de la matrice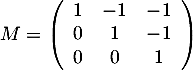 .
.
Montrer que
En déduire l'inverse de la matrice
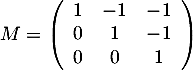 .
.
Correction
![\[(I-A)(I + A + A^2 + \dots + A^{k-1})=I-A^k\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/1.png)
or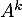 est la matrice nulle, d'où
est la matrice nulle, d'où
![\[(I-A)(I + A + A^2 + \dots + A^k)=I\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/3.png)
ce qui montre que la matrice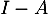 est bien inversible, et d'inverse
est bien inversible, et d'inverse
![\[(I-A)^{-1}=(I + A + A^2 + \dots + A^{k-1})\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/5.png)
On utilise la décomposition précédente pour exprimer la matrice
![\[M=I-A\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/6.png)
avec la matrice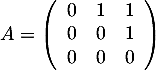 .
On vérifie que cette matrice
.
On vérifie que cette matrice 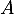 est bien nilpotent:
est bien nilpotent:
![\[\begin{array}{ll}A^2&=\lp\begin{array}{ccc}0&1&1\\0&0&1\\0&0&0\enar\rp\lp\begin{array}{ccc}0&1&1\\0&0&1\\0&0&0\enar\rp\\[2em]&=\lp\begin{array}{ccc}0&0&1\\0&0&0\\0&0&0\enar\rp\enar\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/9.png)
puis que
![\[\begin{array}{ll}A^3&=
\lp\begin{array}{ccc}0&1&1\\0&0&1\\0&0&0\enar\rp\lp\begin{array}{ccc}0&0&1\\0&0&0\\0&0&0\enar\rp\\[2em]
&=\lp\begin{array}{ccc}0&0&0\\0&0&0\\0&0&0\enar\rp\enar\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/10.png)
est la matrice nulle, et on en déduit, dgrâce au résultat précédent, que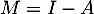 est inversible, d'inverse
est inversible, d'inverse
![\[M^{-1}=(I-A)^{-1}=I+A+A^2\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/12.png)
soit
![\[M^{-1}=\lp\begin{array}{ccc}1&1&2\\0&1&1\\0&0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/13.png)
Correction
On calcule le produit, dont presque tous les termes se télescopentor
ce qui montre que la matrice
On utilise la décomposition précédente pour exprimer la matrice
avec la matrice
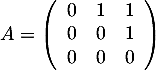 .
On vérifie que cette matrice
.
On vérifie que cette matrice ![\[\begin{array}{ll}A^2&=\lp\begin{array}{ccc}0&1&1\\0&0&1\\0&0&0\enar\rp\lp\begin{array}{ccc}0&1&1\\0&0&1\\0&0&0\enar\rp\\[2em]&=\lp\begin{array}{ccc}0&0&1\\0&0&0\\0&0&0\enar\rp\enar\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/9.png)
puis que
![\[\begin{array}{ll}A^3&=
\lp\begin{array}{ccc}0&1&1\\0&0&1\\0&0&0\enar\rp\lp\begin{array}{ccc}0&0&1\\0&0&0\\0&0&0\enar\rp\\[2em]
&=\lp\begin{array}{ccc}0&0&0\\0&0&0\\0&0&0\enar\rp\enar\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/10.png)
est la matrice nulle, et on en déduit, dgrâce au résultat précédent, que
soit
![\[M^{-1}=\lp\begin{array}{ccc}1&1&2\\0&1&1\\0&0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exnil_c/13.png)
Tag:matrices
Voir aussi:
Quelques devoirs
sur les matrices et calcul matriciel, produit, puissance d'une matrice, définition de l'inverse d'une matrice
sur la factorisation et racines d'un polynôme complexe et matrices et calcul matriciel, diagonalisation et limites de suites
sur binôme de Newton et les racines de l'unité. Calcul de la puissance n-ième d'une matrice
sur les matrices, calcul matriciel et les nombres complexes: géométrie, formes algébriques et exponentielles.
