Exercice complet: 2nd degré, géométrie, formes algébriques et exponentielles
Exercice corrigé - Maths expertes, terminale générale
Énoncé
- Résoudre l'équation
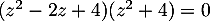 .
.
- On considère les points
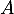 et
et 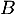 d'affixes respectives
d'affixes respectives
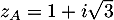 et
et 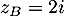 .
.
- Écrire
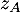 et
et 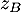 sous forme exponentielle et justifier que les points
sous forme exponentielle et justifier que les points 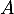 et
et 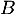 sont sur un cercle de centre
sont sur un cercle de centre  dont on précisera le rayon.
dont on précisera le rayon.
- Faire une figure et placer les points
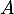 et
et 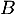 .
.
- Déterminer une mesure de l'angle
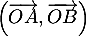 .
.
- Écrire
- On note
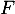 le milieu de
le milieu de ![$[AB]$](/Generateur-Devoirs/Mex/CplxPlan/excplt/15.png) .
.
- Placer le point
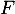 sur la figure précédente et calculer son affixe
sur la figure précédente et calculer son affixe 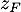 .
.
- Donner une mesure de l'angle
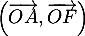 puis en déduire une mesure de l'angle
puis en déduire une mesure de l'angle 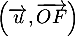 .
.
- Calculer le module de
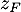 et en déduire l'écriture de
et en déduire l'écriture de 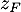 sous forme trigonométrique.
sous forme trigonométrique.
- En déduire la valeur exacte de:
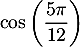
- Placer le point
Correction
Correction
-
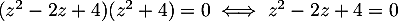 ou
ou 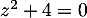
La première équation est du second degré, de discriminant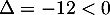 et admet donc deux racines complexes conjuguées:
et admet donc deux racines complexes conjuguées:
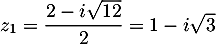 et
et
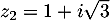 .
.
La deuxième équation est aussi du second degré, mais peut se résoudre plus simplement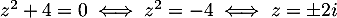 .
.
Ainsi, l'équation a quatre solutions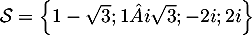 .
.
- On considère les points
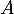 et
et 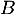 d'affixes respectives
d'affixes respectives
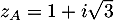 et
et 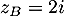 .
.
-
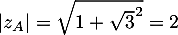 et donc
et donc
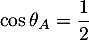 et
et 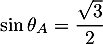 .
On en déduit que
.
On en déduit que 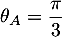 et donc que
et donc que
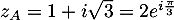 .
.
On a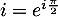 et donc
et donc 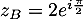 .
.
Comme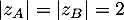 , on en déduit que les points
, on en déduit que les points 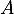 et
et 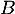 sont sur un cercle de centre
sont sur un cercle de centre  et de rayon 2.
et de rayon 2.
-
![\[\psset{unit=1cm,arrowsize=7pt}
\begin{pspicture}(-3,-2)(3,2)
\psline{->}(-2.6,0)(2.6,0)
\psline{->}(0,-2.6)(0,2.8)
\psline[linewidth=2pt]{->}(0,0)(1,0)\rput(.5,-.3){$\vec{u}$}
\multido{\i=-2+1}{5}{\psline[linestyle=dashed,linewidth=.3pt](\i,-2.2)(\i,2.6)
\rput(\i,-.2){$\i$}}
\multido{\i=-2+1}{5}{\psline[linestyle=dashed,linewidth=.3pt](-2.2,\i)(2.2,\i)
\rput[r](-.1,\i){$\i$}}
\psarc[linecolor=blue](0,0){2}{0}{360}
\rput(0,2){$\tm$}\rput(.2,2.3){$B$}
\rput(1,1.7){$\tm$}\rput(1.3,1.9){$A$}
\psline[linecolor=red,linewidth=1.5pt](0,2)(0,0)(1,1.7)(.5,1.85)(0,2)
\rput(0.5,1.85){$\tm$}\rput(.7,2){$F$}
\end{pspicture}\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/23.png)
- On a
![\[\begin{array}{ll}\lp\overrightarrow{OA},\overrightarrow{OB}\right)
&=\lp\vec{u},\overrightarrow{OB}\rp-\lp\vec{u},\overrightarrow{OB}\rp\\[.6em]
&=\arg(z_B)-\arg(z_A)\\[.6em]
&=\dfrac\pi2-\dfrac\pi3=\dfrac\pi6[2\pi]
\enar\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/24.png)
-
-
- On a
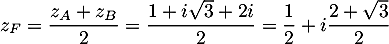
- Comme
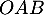 est un triangle isocèle en
est un triangle isocèle en  avec
avec 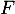 le milieu de
le milieu de ![$[AB]$](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/29.png) , on en déduit que
, on en déduit que 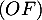 est aussi la bissectrice issue de
est aussi la bissectrice issue de  et donc que
et donc que
![\[\lp\overrightarrow{OA},\overrightarrow{OF}\rp=\dfrac12\lp\overrightarrow{OA},\overrightarrow{OB}\rp=\dfrac\pi{12}\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/32.png)
et ensuite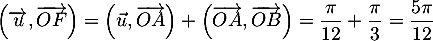 .
.
-
![\[|z_F|=\sqrt{\lp\dfrac12\rp^2+\lp\dfrac{2+\sqrt3}2\rp^2}
=\sqrt{\dfrac{1+(2+\sqrt3)^2}{4}}
=\sqrt{\dfrac{8+4\sqrt3}4}
=\sqrt{2+\sqrt3}
\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/34.png)
et connaissant l'argument de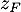 , on a alors trigonométrique:
, on a alors trigonométrique:
![\[z_F=\sqrt{2+\sqrt3}\lp\cos\lp\dfrac{5\pi}{12}\rp+i\sin\lp\dfrac{5\pi}{12}\rp\rp\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/36.png)
- En identifiant la partie réelle de
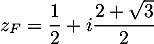 et celle de sa forme trigonométrique, on trouve que
et celle de sa forme trigonométrique, on trouve que
![\[\sqrt{2+\sqrt3}\cos\lp\dfrac{5\pi}{12}\rp=\dfrac12\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/38.png)
d'où
![\[\cos\lp\dfrac{5\pi}{12}\rp=\dfrac1{2\sqrt{2+\sqrt3}}\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/39.png)
- On a
Tag:Plan complexe
Voir aussi:
Quelques devoirs
sur la division euclidienne et les congruences. Nombres complexes: calcul algébrique, inverse et module. Résolution d'une équation.
sur le plan complexe: ensemble de points dans le plan complexe, forme exponentielle et équation du second degré complexe
sur le plan complexe, les nombres complexes en géométrie, et les congruences en arithmétiques. Ecritures algébriques, trigonométrique et exponentielle d'un nombre complexe. Application au calcul de la puissance d'un nombre complexe. Calcul des valeurs exactes des cosinus et sinus de π/12. Congruences et chiffre des unités d'une puissance
sur le plan complexe, les nombres complexes en géométrie, et les congruences en arithmétiques. Ecritures algébriques, trigonométrique et exponentielle d'un nombre complexe. Application au calcul de la puissance d'un nombre complexe. Critère de divisibilité par 19
sur les matrices, calcul matriciel et les nombres complexes: géométrie, formes algébriques et exponentielles.
