Diagonalisation et matrice puissance limite
Exercice corrigé - Maths expertes, terminale générale
Énoncé
On considère les matrices ![$A=\lp\begin{array}{cc}\dfrac13&0\\[1em]-\dfrac13&1\enar\rp$](/Generateur-Devoirs/Mex/Matrices/exdiaglim/1.png) et
et 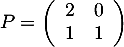 .
.
![$A=\lp\begin{array}{cc}\dfrac13&0\\[1em]-\dfrac13&1\enar\rp$](/Generateur-Devoirs/Mex/Matrices/exdiaglim/1.png) et
et - Montrer que
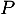 est inversible et donner sa matrice inverse
est inversible et donner sa matrice inverse 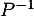 .
.
- Calculer la matrice
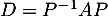 .
.
- Calculer
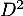 ,
, 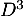 puis donner
puis donner 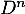 (sans justification supplémentaire).
(sans justification supplémentaire).
- Donner l'expression de
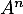 en fonction de
en fonction de 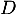 et
et 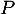 .
.
- On note
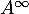 et
et 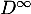 les matrices limites des matrices
les matrices limites des matrices 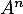 et
et 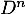 , c'est-à-dire
, c'est-à-dire
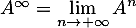 et
et
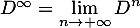 .
.
Déterminer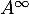 .
.
- On définit les suites
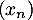 et
et 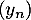 par
par 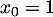 et
et 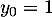 puis par
les relations de récurrence
puis par
les relations de récurrence
![\[\la\begin{array}{ll}x_{n+1}&=\dfrac13x_n\\[.9em]y_{n+1}&=-\dfrac13x_n+y_n\enar\right.\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim/23.png)
Déterminer les limites de ces deux suites.
Correction
Correction
- On a
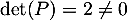 et donc
et donc 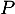 est bien inversible, d'inverse
est bien inversible, d'inverse
![\[P^{-1}=\dfrac12\lp\begin{array}{cc}1&0\\-1&2\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/3.png)
- On calcule les deux produits, successivement,
![\[\begin{array}{ll}D&=P^{-1}AP\\
&=\dfrac12\lp\begin{array}{cc}1&0\\-1&2\enar\right)
\lp\begin{array}{cc}\dfrac13&0\\[1em]-\dfrac13&1\enar\right) P\\[2em]
&=\dfrac12\lp\begin{array}{cc}\dfrac13&0\\[1em]-1&2\enar\rp\lp\begin{array}{cc}2&0\\1&1\enar\rp\\[2em]
&=\dfrac12\lp\begin{array}{cc}\dfrac23&0\\[1em]0&2\enar\right)
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/4.png)
et on trouve donc la matrice diagonale![$D=\lp\begin{array}{cc}\dfrac13&0\\[1em]0&1\enar\rp$](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/5.png)
- On calcule facilement que
![\[D^2=\lp\begin{array}{cc}\lp\dfrac13\rp^2&0\\[1em]0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/6.png)
et
![\[D^3=\lp\begin{array}{cc}\lp\dfrac13\rp^3&0\\[1em]0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/7.png)
qu'on généralise à
![\[D^n=\lp\begin{array}{cc}\lp\dfrac13\rp^n&0\\[1em]0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/8.png)
- On a la relation
![\[D=P^{-1}AP \iff PDP^{-1}=A\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/9.png)
et alors
![\[\begin{array}{ll}A^n&=\underbrace{A\,A\,A\,\dots\,A}_{n \text{termes}}\\[1.6em]
&=PA\underbrace{P^{-1}P}_{=I_2}D\underbrace{P^{-1}P}_{=I_2}DP{-1}\dots\,\underbrace{P^{-1}P}_{=I_2}DP^{-1}\\[1.6em]
&=PD^nP^{-1}
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/10.png)
- Comme
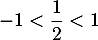 , on a
, on a 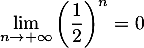 et donc
et donc
![\[D^\infty=\lp\begin{array}{cc}0&0\\0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/13.png)
et alors, en passant à la limite dans les produits
![\[\begin{array}{ll}A^\infty&=PD^\infty P^{-1}\\
&=\lp\begin{array}{cc}2&0\\1&1\enar\rp\lp\begin{array}{cc}0&0\\0&1\enar\rp P^{-1}\\[1.2em]
&=\lp\begin{array}{cc}0&0\\0&1\enar\rp\dfrac12\lp\begin{array}{cc}1&0\\-1&2\enar\rp\\[1.2em]
&=\dfrac12\lp\begin{array}{cc}0&0\\-1&2\enar\rp\\[1.2em]
&=\lp\begin{array}{cc}0&0\\-\dfrac12&1\enar\right)
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/14.png)
- On pose
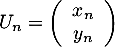 , et alors on a
, et alors on a
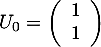 et les relations de récurrence s'écrivent matriciellement
et les relations de récurrence s'écrivent matriciellement
![\[U_{n+1}=AU_n\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/17.png)
Il s'agit donc d'une suite géométrique, et on a directement pour tout entier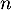 ,
,
![\[U_n=A^nU_0\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/19.png)
et, avec les calculs précédents, on trouve la limite
![\[\begin{array}{ll}\dsp\lim_{n\to+\infty}U_n&=D^\infty U_0\\
&=\lp\begin{array}{cc}0&0\\-\dfrac12&1\enar\rp\lp\begin{array}{c}1\\1\enar\rp\\[1.5em]
&=\lp\begin{array}{c}0\\\dfrac12\enar\right)
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/20.png)
c'est-à-dire, en revenant aux suites de l'énoncé,
![\[\begin{array}{ll}\dsp\lim_{n\to+\infty}x_n=0\\\dsp\lim_{n\to+\infty}y_n=\dfrac12\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/21.png)
Tag:matrices
Voir aussi:
Quelques devoirs
sur les matrices et calcul matriciel, produit, puissance d'une matrice, définition de l'inverse d'une matrice
sur la factorisation et racines d'un polynôme complexe et matrices et calcul matriciel, diagonalisation et limites de suites
sur binôme de Newton et les racines de l'unité. Calcul de la puissance n-ième d'une matrice
sur les matrices, calcul matriciel et les nombres complexes: géométrie, formes algébriques et exponentielles.
