Intégration et calcul intégral: annales de bac et corrections
Terminale générale, spécialité mathématiques
Annales de bac: sujets et corrigés d'exercices posés au baccalauréat en mathématiques sur les intégrales
Exercice 1: Bac 2022: QCM, limite, convexité, primitive
Cet exercice est un questionnaire à choix multiple.
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Les six questions sont indépendantes
Cacher la correction
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Les six questions sont indépendantes
- La courbe représentative de la fonction
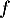 définie sur
définie sur 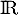 par
par 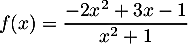 admet pour asymptote
la droite d'équation:
admet pour asymptote
la droite d'équation:
a.
b.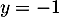
c.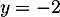
d.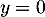
- Soit
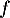 la fonction définie sur
la fonction définie sur 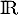 par
par 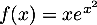 .
.
La primitive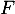 de
de 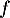 sur
sur 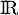 qui vérifie
qui vérifie  est définie par :
est définie par :
a.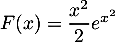
b.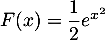
c.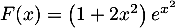 ;
;
d.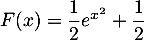
- On donne ci-contre la représentation graphique
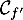 de la fonction dérivée
de la fonction dérivée 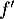 d'une fonction
d'une fonction  définie sur
définie sur 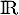 .
.
(10,1)
\psaxes[linewidth=1.25pt,Dx=11,Dy=11](0,0)(-0.5,-5)(10,1)
\psecurve[linewidth=1.25pt,linecolor=blue](-0.3,-6)(-0.2,-5)(0,-4)(1,-1.2)(2,0)(3,0.45)(4,0.5)(5,0.45)(6,0.4)(10,0.1)(11,0.08)
\uput[d](1,0){\footnotesize 1}\uput[d](2,0){\footnotesize 2}\uput[dl](0,0){\footnotesize 0}\uput[d](0,1){\footnotesize 1}
\uput[r](0.4,3.5){$\mathcal{C}_{f'}$}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/23.png)
On peut affirmer que la fonction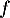 est :
est :
a. concave sur![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/25.png)
b. convexe sur![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/26.png)
c. convexe sur [0 ; 2]
d. convexe sur
- Parmi les primitives de la fonction
 définie sur
définie sur  par
par 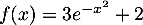 :
:
a. toutes sont croissantes sur
b. toutes sont décroissantes sur
c. certaines sont croissantes sur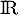 et d'autres
décroissantes sur
et d'autres
décroissantes sur 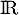
d. toutes sont croissantes sur![$]-\infty~;~0]$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/35.png) et
décroissantes sur
et
décroissantes sur 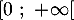
- La limite en
 de la fonction
de la fonction  définie sur l'intervalle
définie sur l'intervalle ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/39.png) par
par  est égale à :
est égale à :
a. ;
;
b.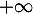 ;
;
c.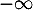
d.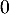
- L'équation
 admet dans
admet dans 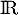 :
:
a. trois solutions;
b. deux solutions;
c. une seule solution;
d. aucune solution.
Correction exercice 1
- c.
On a
![\[\begin{array}{ll}f(x) &= \dfrac{-2x^2 + 3x - 1}{x^2 + 1}\\[1em]
&=\dfrac{-2x^2\lp1-\frac3{2x}+\frac1{2x^2}\right)}{x^2\lp1+\frac1{x^2}\right)}\\[1em]
&=-2\dfrac{1-\frac3{2x}+\frac1{2x^2}}{1+\frac1{x^2}}
\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/1.png)
d'où
![\[\lim_{x\to+\infty}f(x)=-2\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/2.png)
et donc la droite d'équation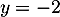 est asymptote.
est asymptote.
- d.
On peut par exemple dériver chacune des propositions, seule la b. et la d. convienne.
Comme on veut de plus que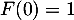 , seule la réponse d. convient finalement.
, seule la réponse d. convient finalement.
- c.
Une fonction est convexe lorsque sa dérivée est croissante (et donc dérivée seconde positive).
Ici on peut conjecturer que la fonction est convexe sur![$]-\infty;3]$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/5.png) environ,
et donc en particulier sur
environ,
et donc en particulier sur ![$[0;2]$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/6.png) .
.
- a.
Les primitives
 de
de 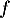 vérifient
vérifient  .
En particulier, comme
.
En particulier, comme 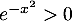 sur
sur  ,
on a
,
on a 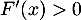 et donc
et donc 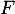 est nécessairement strictement croissante sur
est nécessairement strictement croissante sur 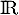 .
.
- d.
On a
![\[f(x) = \dfrac{2\ln x}{3x^2 + 1}
=\dfrac{\ln(x)}{x^2}\tm\dfrac{2}{3+\frac1{x^2}}\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/15.png)
avec, par croissances comparées
![\[\lim_{x\to+\infty}\dfrac{\ln(x)}{x^2}=0\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/16.png)
et donc
![\[\lim_{x\to+\infty}f(x)=0\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/17.png)
- c.
On pose et alors l'équation se réécrit
et alors l'équation se réécrit
![\[X^2+X-12=0\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/19.png)
c'est une équation du second degré de discriminant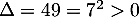 qui admet donc deux solutions réelles distinctes
qui admet donc deux solutions réelles distinctes
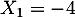 et
et 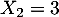 .
.
On revient alors à l'équation de départ:-
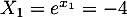 qui est impossible, car
qui est impossible, car  pour tout réel
pour tout réel 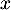
-
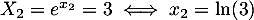
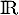 .
.
-
Cacher la correction
Exercice 2: Bac 2019, Métropole: Intégrale gaussienne, et méthode de Monté Carlo
On donne ci-dessous la représentation graphique 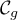 dans un repère orthogonal d'une fonction
dans un repère orthogonal d'une fonction 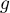 définie et continue sur
définie et continue sur 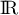 .
La courbe
.
La courbe 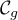 est symétrique par rapport à l'axe des ordonnées
et se situe dans le demi-plan
est symétrique par rapport à l'axe des ordonnées
et se situe dans le demi-plan 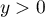 .
.
(\n,1.2)}
\multido{\n=-0.2+0.2}{8}{\psline[linewidth=0.2pt](-2,\n)(2,\n)}
\psaxes[linewidth=1.25pt,Dx=0.5,Dy=0.2](0,0)(-2,-0.19)(2,1.2)
\uput[d](-0.08,-0.02){$0$}
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-2}{2}{1 2.71828 x dup mul exp div}
%\psGauss[mue=0,sigma=0.75,linewidth=1.25pt,linecolor=blue]{-2}{2}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/6.png)
Pour tout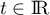 on pose:
on pose:
![\[G(t)=\int_0^t g(u) du\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/8.png)
Partie A
Les justifications des réponses aux questions suivantes pourront s'appuyer sur des considérations graphiques.
Dans la suite du problème, la fonction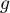 est définie sur
est définie sur 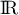 par
par 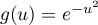 .
.
Partie B
Partie C
On rappelle que la fonction est définie sur
est définie sur  par
par 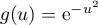 et que la fonction
et que la fonction 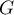 est définie sur
est définie sur 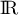 par :
par :
![\[G(t) =\int_0^t g(u) du\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/68.png)
On se propose de déterminer une majoration de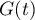 pour
pour 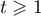 .
.
(\n,1.2)}
\multido{\n=-0.2+0.2}{8}{\psline[linewidth=0.2pt](-2,\n)(2,\n)}
\psaxes[linewidth=1.25pt,Dx=0.5,Dy=0.2](0,0)(-2,-0.19)(2,1.2)
\uput[d](-0.08,-0.02){$0$}
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-2}{2}{1 2.71828 x dup mul exp div}
%\psGauss[mue=0,sigma=0.75,linewidth=1.25pt,linecolor=blue]{-2}{2}
\pscustom[fillstyle=vlines]{\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1}{1 2.71828 x dup mul exp div}
\psline(1,0)(0,0)}
\pspolygon[linecolor=red,linewidth=2pt](0,0)(0,1)(0.5,1)(0.5,0.8)(1,0.8)(1,0)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/1.png)
Partie B
Partie C
Cacher la correction
(\n,1.2)}
\multido{\n=-0.2+0.2}{8}{\psline[linewidth=0.2pt](-2,\n)(2,\n)}
\psaxes[linewidth=1.25pt,Dx=0.5,Dy=0.2](0,0)(-2,-0.19)(2,1.2)
\uput[d](-0.08,-0.02){$0$}
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-2}{2}{1 2.71828 x dup mul exp div}
%\psGauss[mue=0,sigma=0.75,linewidth=1.25pt,linecolor=blue]{-2}{2}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/6.png)
Pour tout
Partie A
Les justifications des réponses aux questions suivantes pourront s'appuyer sur des considérations graphiques.
- La fonction
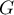 est-elle croissante sur
est-elle croissante sur 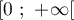 ? Justifier.
? Justifier.
- Justifier graphiquement l'inégalité
 .
.
- La fonction
 est-elle positive sur
est-elle positive sur  ? Justifier.
? Justifier.
Dans la suite du problème, la fonction
Partie B
- Étude de
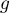
- Déterminer les limites de la fonction
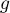 aux bornes
de son ensemble de définition.
aux bornes
de son ensemble de définition.
- Calculer la fonction dérivée de
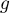 et en déduire
le tableau de variations de
et en déduire
le tableau de variations de 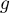 sur
sur 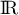 .
.
- Préciser le maximum de
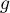 sur
sur 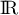 . En déduire que
. En déduire que 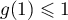 .
.
- Déterminer les limites de la fonction
- On note
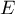 l'ensemble des points
l'ensemble des points 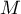 situés entre
la courbe
situés entre
la courbe 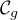 , l'axe des abscisses et les droites d'équation
, l'axe des abscisses et les droites d'équation
 et
et  . On appelle
. On appelle 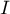 l'aire de cet ensemble.
l'aire de cet ensemble.
On rappelle que:
![\[I=G(1)=\int_0^1 g(u) du\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/31.png)
On souhaite estimer l'aire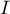 par la méthode dite "de Monte-Carlo"
décrite ci-dessous.
par la méthode dite "de Monte-Carlo"
décrite ci-dessous.
- On choisit un point
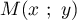 en tirant au hasard de façon
indépendante ses coordonnées
en tirant au hasard de façon
indépendante ses coordonnées 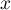 et
et 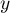 selon la loi uniforme sur
l'intervalle
selon la loi uniforme sur
l'intervalle ![$[0~;~ 1]$](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/36.png) . On admet que la
probabilité que le point
. On admet que la
probabilité que le point 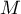 appartienne à l'ensemble
appartienne à l'ensemble 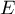 est égale à
est égale à 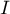 .
.
- On répète
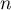 fois l'expérience du choix d'un point
fois l'expérience du choix d'un point 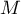 au hasard.
On compte le nombre
au hasard.
On compte le nombre 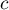 de points appartenant à l'ensemble
de points appartenant à l'ensemble 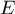 parmi
les
parmi
les 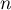 points obtenus.
points obtenus.
- La fréquence
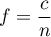 est une estimation de la valeur de
est une estimation de la valeur de 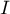 .
.
- La figure ci-dessous illustre la méthode présentée pour
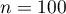 .
Déterminer la valeur de
.
Déterminer la valeur de 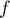 correspondant à ce graphique.
correspondant à ce graphique.
(0,0)(1,1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1}{1 2.71828 x dup mul exp div}
\psdots(0.1,0.98)(0.05,0.02)(0.12,0.9)(0.22,0.83)(0.32,0.82)(0.37,0.815)(0.09,0.76)(0.22,0.69)(0.35,0.67)(0.11,0.7)(0.18,0.53)(0.24,0.63)(0.57,0.61)(0.64,0.61)(0.65,0.6)(0.21,0.58)
(0.48,0.55)(0.64,0.55)(0.66,0.53)(0.7,0.5)(0.57,0.44)(0.72,0.44)(0.77,0.44)(0.85,0.47)
(0.13,0.46)(0.75,0.39)(0.54,0.41)(0.09,0.28)(0.27,0.29)(0.69,0.36)(0.7,0.37)(0.08,0.35)
(0.28,0.28)(0.46,0.25)(0.47,0.23)(0.57,0.28)(0.7,0.28)(0.96,0.25)(0.3,0.23)(0.46,0.23)
(0.54,0.21)(0.93,0.2)(0.96,0.23)(0.025,0.16)(0.035,0.16)(0.18,0.18)(0.28,0.16)(0.41,0.12)
(0.63,0.16)(0.95,0.1)(0.45,0.13)(0.74,0.17)(0.94,0.12)(0.96,0.15)(0.08,0.04)(0.29,0.04)
(0.01,0.02)(0.12,0.02)(0.51,0.01)(0.58,0)(0.92,0)(0.28,0.4)(0.3,0.42)(0.32,0.45)
(0.35,0.5)(0.37,0.55)(0.39,0.57)(0.41,0.5)(0.48,0.41)(0.79,0.2)(0.76,0.15)(0.8,0.1)
(0.85,0.26)(0.9,0.4)(0.44,0.65)(0.44,0.48)(0.57,0.63)
\psdots[dotstyle=o](0.29,0.95)(0.57,0.98)(0.59,0.95)(0.79,0.92)(0.9,0.99)(0.49,0.8)(0.68,0.9)(0.79,0.91)(0.81,0.92)(0.43,0.85)(0.77,0.79)(0.94,0.77)(0.84,0.68)(0.87,0.64)(0.85,0.61)(0.83,0.59)
(0.74,0.77)(0.97,0.69)(0.975,0.495)(0.92,0.47)(0.93,0.44)(0.6,0.8)(0.68,0.78)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/49.png)
- L'exécution de l'algorithme ci-dessous utilise
la méthode de Monte-Carlo décrite précédemment pour déterminer une valeur
du nombre
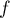 .
Recopier et compléter cet algorithme.
.
Recopier et compléter cet algorithme.
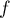 ,
, 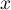 et
et 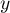 sont des nombres réels,
sont des nombres réels, 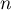 ,
, 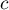 et
et  sont
des entiers naturels.
sont
des entiers naturels.
ALEA est une fonction qui génère aléatoirement un nombre compris entre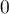 et
et  .
.
![\[\fbox{\begin{minipage}{8cm}
$c \gets 0$\\
Pour $i$ variant de $1$ \`a $n$ faire :\\
\hspace*{2.cm}$x \gets$ ALEA\\
\hspace*{2.cm}$y \gets$ ALEA\\
\hspace*{1cm}Si $y \leqslant \ldots$ alors\\
\hspace*{2.cm}$c \gets \ldots$\\
\hspace*{1cm}fin Si\\
fin Pour\\
\hspace{2.5cm}$f \gets \ldots$\\
\end{minipage}}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/59.png)
- Une exécution de l'algorithme pour
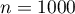 donne
donne 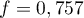 .
En déduire un intervalle de confiance, au niveau de confiance de 95 %,
de la valeur exacte de
.
En déduire un intervalle de confiance, au niveau de confiance de 95 %,
de la valeur exacte de 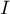 .
.
- On choisit un point
Partie C
On rappelle que la fonction
On se propose de déterminer une majoration de
- Un résultat préliminaire.
On admet que, pour tout réel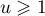 , on a
, on a
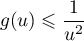 .
.
En déduire que, pour tout réel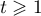 , on a :
, on a :
![\[\int_1^t g(u) du \leqslant 1 - \dfrac1t\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/74.png)
- Montrer que, pour tout réel
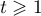 ,
,
![\[G(t) \leqslant 2 - \dfrac1t\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre/76.png)
Que peut-on dire de la limite éventuelle de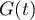 lorsque
lorsque 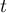 tend vers
tend vers 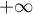 ?
?
Correction exercice 2
(\n,1.2)}
\multido{\n=-0.2+0.2}{8}{\psline[linewidth=0.2pt](-2,\n)(2,\n)}
\psaxes[linewidth=1.25pt,Dx=0.5,Dy=0.2](0,0)(-2,-0.19)(2,1.2)
\uput[d](-0.08,-0.02){$0$}
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-2}{2}{1 2.71828 x dup mul exp div}
%\psGauss[mue=0,sigma=0.75,linewidth=1.25pt,linecolor=blue]{-2}{2}
\pscustom[fillstyle=vlines]{\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1}{1 2.71828 x dup mul exp div}
\psline(1,0)(0,0)}
\pspolygon[linecolor=red,linewidth=2pt](0,0)(0,1)(0.5,1)(0.5,0.8)(1,0.8)(1,0)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/1.png)
- La fonction
 est l'intégrale d'une fonction positive
et est donc croissante sur l'intervalle
est l'intégrale d'une fonction positive
et est donc croissante sur l'intervalle 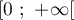 .
.
Algébriquement, on sait que est la primitive de
est la primitive de 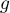 qui s'annule en 1.
On a donc en particulier
qui s'annule en 1.
On a donc en particulier 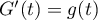 avec
avec 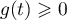 d'après le graphique.
Ainsi,
d'après le graphique.
Ainsi, 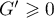 et
et 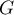 est croissante sur
est croissante sur  .
.
-
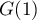 est égale à l'aire, en unités d'aire,
de la surface hachurée sur le graphique.
Cette aire est inférieure à celle des deux rectangles tracés en rouge,
dont l'aire vaut
est égale à l'aire, en unités d'aire,
de la surface hachurée sur le graphique.
Cette aire est inférieure à celle des deux rectangles tracés en rouge,
dont l'aire vaut 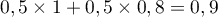 , et on a donc ainsi
, et on a donc ainsi
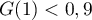 .
.
- Comme
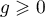 on a, par positivité de l'intégrale, que
pour tout
on a, par positivité de l'intégrale, que
pour tout 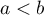 ,
,
![\[\int_a^b g(u)du\geqslant0\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/16.png)
Ainsi, pout tout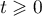 ,
,
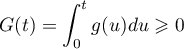 .
.
Par contre, si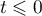 , alors
, alors
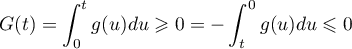 .
.
Ainsi,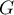 est négative sur
est négative sur 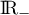 et positive sur
et positive sur 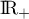 .
.
Partie B
-
- Comme
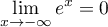 , on a par composition des limites,
, on a par composition des limites,
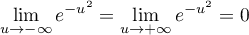 ,
,
c'est-à-dire
![\[\lim_{u\to-\infty} g(u) = \lim_{u \to + \infty} g(u) = 0\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/26.png)
-
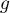 est dérivable sur
est dérivable sur 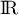 comme composée de la fonction exponentielle
et de la fonction carré, toutes deux dérivables sur
comme composée de la fonction exponentielle
et de la fonction carré, toutes deux dérivables sur 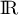 ,
avec,
,
avec,
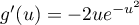 .
.
Comme pour tout réel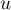 , on a
, on a 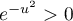 , on a donc
, on a donc
![\[\begin{tabular}{|c|ccccc|}\hline
$u$&$-\infty$&&0&&$+\infty$\\\hline
$-2u$&&$+$&0&$-$&\\\hline
$e^{-u^2}$&&$+$&$|$&$+$&\\\hline
$g'(u)$&&$+$&0&$-$&\\\hline
&&&1&&\\
$g$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&0&&&&0\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/33.png)
- Comme trouvé dans le tableau de variation précédent,
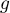 atteint son maximum en
atteint son maximum en  , et qui vaut
, et qui vaut 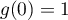 .
Ceci signifie aussi que pour tout réel
.
Ceci signifie aussi que pour tout réel 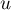 on a
on a 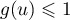 ,
et en particulier pour
,
et en particulier pour  , on a
, on a 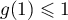 .
.
- Comme
-
- On compte 23 points au dessus de la courbe, donc 77 en dessous,
et donc
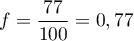 .
.
-
![\[\fbox{\begin{minipage}{8cm}
$c \gets 0$\\
Pour $i$ variant de $1$ \`a $n$ faire :\\
\hspace*{2.cm}$x \gets$ ALEA\\
\hspace*{2.cm}$y \gets$ ALEA\\
\hspace*{1cm}Si $y \leqslant \text{e}^{-x^2}$ alors\\
\hspace*{2.cm}$c \gets c + 1$\\
\hspace*{1cm}fin Si\\
fin Pour\\
\hspace*{2.5cm}$f \gets \dfrac{c}{n}$\\
\end{minipage}}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/42.png)
- Pour
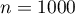 et
et 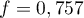 , l'intervalle de confiance
de la valeur exacte de
, l'intervalle de confiance
de la valeur exacte de 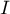 ,
au niveau de confiance de 95 %, est
,
au niveau de confiance de 95 %, est
![\[\left[ f-\dfrac1{\sqrt{n}}~;~f-\dfrac1{\sqrt{n}}\right]
=\bigl[0,725~;~0,789\bigr]\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/46.png)
- On compte 23 points au dessus de la courbe, donc 77 en dessous,
et donc
Partie C
- Comme l'intégrale conserve l'ordre, on a
![\[g(u) \leqslant \dfrac{1}{u^2} \Longrightarrow
\int_1^t g(u) du \leqslant \int_1^t\dfrac{1}{u^2} du\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/47.png)
ce ui nous donne le résultat cherché car
![\[\int_1^t\dfrac{1}{u^2} du=\Bigl[-\dfrac1u\Bigr]_1^t=-\dfrac1t+1\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/48.png)
- On a, en utilisant la relation de Chasles,
![\[\begin{array}{ll}G(t)&=\dsp\int_0^tg(u)du \\[1.2em]
&=\dsp\int_0^1 g(u) du + \int_1^t g(u) du\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/49.png)
Or, on a vu que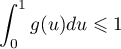 et par ailleurs, dans la question précédente, que
et par ailleurs, dans la question précédente, que
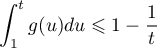 ,
d'où par somme:
,
d'où par somme:
![\[G(t) \leqslant 1+ 1 - \dfrac1t=2-\dfrac1t\]](/Generateur-Devoirs/TS/ChapIntegration/ex2019-Metropole-septembre_c/52.png)
Comme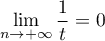 ,
si la limite de
,
si la limite de 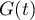 lorsque
lorsque 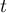 tend vers
tend vers 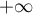 existe, alors
elle est inférieure ou égale à 2.
existe, alors
elle est inférieure ou égale à 2.
Cacher la correction
Exercice 3: Bac 2016, Amérique du nord: Un récupérateur d'eau: logarithme, tangente, primitive, intégrale, TVI et algorithme: dichotomie
Un particulier veut faire fabriquer un récupérateur d'eau.
Ce récupérateur d'eau est une cuve qui doit respecter le cahier des
charges suivant:
Cette cuve est schématisée ci-dessous.
![$$(-1.8,-0.5)(7,5)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\pspolygon(2,0)(2,1.8)(-1.3,2.5)(-1.3,0.7)
\rput(-3.3,0.7){\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}}
\psline(2.1,2.7)(5.4,2)
\psline(-1.3,2.5)(2.1,2.7)
\psline(2,1.8)(5.4,2)
\psline[linewidth=0.5pt](2,1.8)(2,3)\psline[linewidth=0.5pt](-1.3,2.5)(-1.3,3.7)
\psset{arrowsize=2pt 3}
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(2,3)(-1.3,3.7)
\psline[linewidth=0.5pt](2,1.8)(1.2,1.75)\psline[linewidth=0.5pt](2,0)(1.2,-0.05)
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(1.2,1.75)(1.2,-0.05)
\uput[l](1.2,0.85){2 m}\uput[u](1.35,3.35){5 m}
$$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/1.png)
La partie incurvée est modélisée par la courbe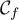 de la
fonction
de la
fonction 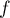 sur l'intervalle
sur l'intervalle ![$[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/4.png) définie par:
définie par:
![\[f(x)=x\ln \lp\dfrac{x}{2}\rp-x+2.\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/5.png)
La courbe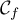 est représentée ci-dessous dans un repère
orthonormé d'unité 1m et constitue une vue de profil de la cuve.
est représentée ci-dessous dans un repère
orthonormé d'unité 1m et constitue une vue de profil de la cuve.
On considère les points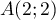 ,
, 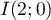 et
et 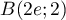 .
.
(-0.2,-0.25)(6,2.5)
\psaxes[linewidth=1.25pt](0,0)(0,0)(6,2.5)
\uput[u](2.8,0.2){$\mathcal{C}_f$}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\psframe[fillstyle=solid,fillcolor=lightgray](2,2)
\psdots(2,2)(5.437,2)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psplot[plotpoints=4000]{3}{5.8}{x 2 add 5.437 sub}
\uput[u](2,2){$A$}
\uput[u](5.437,2){$B$}
\uput[ul](5.75,2.2){$\mathcal{T}$}
\uput[dl](2,0){$I$}
\uput[dr](3.437,0){$D$}
\rput(1,1){Terrain}
\rput(3.2,1.2){Cuve}
\rput(4.7,0.5){Terrain}
\psline[linestyle=dotted,linewidth=1.5pt](2,2)(5.437,2)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/10.png)
Partie A L'objectif de cette partie est d'évaluer le volume de la cuve.
Partie B Pour tout réel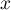 compris
entre
compris
entre 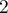 et
et 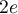 , on note
, on note 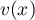 le volume d'eau, exprimé en m3, se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est
égale à
le volume d'eau, exprimé en m3, se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est
égale à 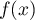 .
.
On admet que, pour tout réel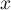 de l'intervalle [2 ; 2e],
de l'intervalle [2 ; 2e],
![\[v(x) = 5\left[\dfrac{x^2}{2}\ln \left( \dfrac{x}{2}\right) - 2x\ln\left( \dfrac{x}{2}\right) - \dfrac{x^2}{4} + 2x - 3\right].\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/49.png)
{\n}}
}
\pspolygon[fillstyle=solid,fillcolor=gray](2,0.1)(2,1.5)(0.35,2.3)(0.35,0.9)
\pspolygon[fillstyle=solid,fillcolor=gray](2,1.5)(0.35,2.3)(3.37,2.47)(5.08,1.7)
\pscustom[fillstyle=solid,fillcolor=gray]{
\pscurve(2,0.1)(3,0.316)(4,0.87)(5.08,1.75)
\psline(5.08,1.75)(2,1.5)
}
\pspolygon(5.437,2.1)(2,1.85)(0.35,2.7)(3.787,2.95)
\psline(2,1.85)(2,1.5)
\psline(0.35,2.7)(0.35,2.3)
\pscurve(0.35,0.9)(1.35,1.16)(2.35,1.72)(3.35,2.5)(3.787,2.95)
\psline[linestyle=dotted,linewidth=1.5pt](5.08,0.2)(5.08,1.75)(0,1.37)
\uput[d](5.2,0.3){$x$}
\uput[l](0,1.37){$f(x)$}
\multido{\n=0+1}{4}{\uput[l](0,\n){\n}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/50.png)
Bac S - Amérique du nord, 1er juin 2016 6 points
Partie A
Partie B
Cacher la correction
- elle doit être située à deux mètres de sa maison;
- la profondeur maximale doit être de deux mètres;
- elle doit mesurer cinq mètres de long;
- elle doit épouser la pente naturelle du terrain.
Cette cuve est schématisée ci-dessous.
![$$(-1.8,-0.5)(7,5)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\pspolygon(2,0)(2,1.8)(-1.3,2.5)(-1.3,0.7)
\rput(-3.3,0.7){\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}}
\psline(2.1,2.7)(5.4,2)
\psline(-1.3,2.5)(2.1,2.7)
\psline(2,1.8)(5.4,2)
\psline[linewidth=0.5pt](2,1.8)(2,3)\psline[linewidth=0.5pt](-1.3,2.5)(-1.3,3.7)
\psset{arrowsize=2pt 3}
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(2,3)(-1.3,3.7)
\psline[linewidth=0.5pt](2,1.8)(1.2,1.75)\psline[linewidth=0.5pt](2,0)(1.2,-0.05)
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(1.2,1.75)(1.2,-0.05)
\uput[l](1.2,0.85){2 m}\uput[u](1.35,3.35){5 m}
$$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/1.png)
La partie incurvée est modélisée par la courbe
La courbe
On considère les points
(-0.2,-0.25)(6,2.5)
\psaxes[linewidth=1.25pt](0,0)(0,0)(6,2.5)
\uput[u](2.8,0.2){$\mathcal{C}_f$}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\psframe[fillstyle=solid,fillcolor=lightgray](2,2)
\psdots(2,2)(5.437,2)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psplot[plotpoints=4000]{3}{5.8}{x 2 add 5.437 sub}
\uput[u](2,2){$A$}
\uput[u](5.437,2){$B$}
\uput[ul](5.75,2.2){$\mathcal{T}$}
\uput[dl](2,0){$I$}
\uput[dr](3.437,0){$D$}
\rput(1,1){Terrain}
\rput(3.2,1.2){Cuve}
\rput(4.7,0.5){Terrain}
\psline[linestyle=dotted,linewidth=1.5pt](2,2)(5.437,2)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/10.png)
Partie A L'objectif de cette partie est d'évaluer le volume de la cuve.
- Justifier que les points
 et
et  appartiennent à la courbe
appartiennent à la courbe
 et que l'axe des abscisses est tangent à la courbe
et que l'axe des abscisses est tangent à la courbe
 au point
au point  .
.
- On note
 la tangente à la courbe
la tangente à la courbe 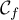 au
point
au
point  , et
, et 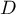 le point d'intersection de la droite
le point d'intersection de la droite 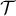 avec l'axe des abscisses.
avec l'axe des abscisses.
- Déterminer une équation de la droite
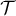 et en
déduire les coordonnées de
et en
déduire les coordonnées de  .
.
- On appelle
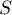 l'aire du domaine délimité par la courbe
l'aire du domaine délimité par la courbe
 , les droites d'équations
, les droites d'équations 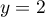 ,
,  et
et  .
.
 peut être encadrée par l'aire du triangle
peut être encadrée par l'aire du triangle  et celle du
trapèze
et celle du
trapèze  .
.
Quel encadrement du volume de la cuve peut-on en déduire ?
- Déterminer une équation de la droite
-
- Montrer que, sur l'intervalle
![$[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/31.png) ,
la fonction
,
la fonction 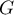 définie par
définie par
![\[G(x)=\dfrac{x^2}{2}\ln \lp\dfrac{x}{2}\rp-\dfrac{x^2}{4}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/33.png)
est une primitive de la fonction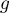 définie par
définie par
 .
.
- En déduire une primitive
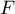 de la fonction
de la fonction 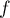 sur
l'intervalle
sur
l'intervalle ![$[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/38.png) .
.
- Déterminer la valeur exacte de l'aire
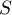 et en déduire une
valeur approchée du volume
et en déduire une
valeur approchée du volume 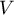 de la cuve au m3 près.
de la cuve au m3 près.
- Montrer que, sur l'intervalle
Partie B Pour tout réel
On admet que, pour tout réel
{\n}}
}
\pspolygon[fillstyle=solid,fillcolor=gray](2,0.1)(2,1.5)(0.35,2.3)(0.35,0.9)
\pspolygon[fillstyle=solid,fillcolor=gray](2,1.5)(0.35,2.3)(3.37,2.47)(5.08,1.7)
\pscustom[fillstyle=solid,fillcolor=gray]{
\pscurve(2,0.1)(3,0.316)(4,0.87)(5.08,1.75)
\psline(5.08,1.75)(2,1.5)
}
\pspolygon(5.437,2.1)(2,1.85)(0.35,2.7)(3.787,2.95)
\psline(2,1.85)(2,1.5)
\psline(0.35,2.7)(0.35,2.3)
\pscurve(0.35,0.9)(1.35,1.16)(2.35,1.72)(3.35,2.5)(3.787,2.95)
\psline[linestyle=dotted,linewidth=1.5pt](5.08,0.2)(5.08,1.75)(0,1.37)
\uput[d](5.2,0.3){$x$}
\uput[l](0,1.37){$f(x)$}
\multido{\n=0+1}{4}{\uput[l](0,\n){\n}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/50.png)
- Quel volume d'eau, au m3 près, y a-t-il dans la cuve lorsque la hauteur d'eau dans la cuve est de un mètre ?
- On rappelle que
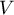 est le volume total de la cuve,
est le volume total de la cuve,  est la
fonction définie en début d'exercice et
est la
fonction définie en début d'exercice et  la fonction définie dans
la partie B.
la fonction définie dans
la partie B.
On considère l'algorithme ci-dessous.
Interpréter le résultat que cet algorithme permet d'afficher.
![\[\begin{tabular}{|ll|}\hline
Variables:&$a$ est un r\'eel\\
&$b$ est un r\'eel\\
Traitement:&$a$ prend la valeur 2\\
&$b$ prend la valeur 2 e\\
&Tant que $v(b) - v(a) > 10^{-3}$ faire :\\
&\hspace{0.4cm}\begin{tabular}{|l}
$c$ prend la valeur $(a+b)/2$\\
Si $v(c) < V/2$, alors :\\
\hspace{0.4cm}\begin{tabular}{|l}
$a$ prend la valeur c\\
\end{tabular}\\
Sinon\\
\hspace{0.4cm} \begin{tabular}{|l}
$b$ prend la valeur $c$\\
\end{tabular}\\
Fin Si\\
\end{tabular}\\
&Fin Tant que\\
Sortie: &Afficher $f(c)$\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/55.png)
Correction exercice 3
Bac S - Amérique du nord, 1er juin 2016 6 points
Partie A
- On a
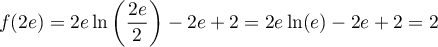 ,
car
,
car 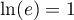 , et donc
, et donc  .
.
De même, ,
car
,
car  , et donc
, et donc  .
.
De plus, en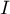 le coefficient directeur de la tangente à
le coefficient directeur de la tangente à
 est
est  .
.
On a, pour tout ,
,
 ,
soit
,
soit 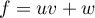 ,
avec
,
avec  , donc
, donc 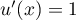 ,
,
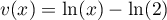 , donc
, donc 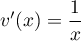 ,
et
,
et 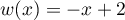 , donc
, donc 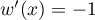 .
.
On a alors,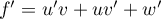 ,
soit
,
soit
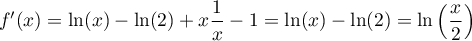 .
.
Ainsi, la tangente à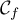 en
en 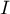 a pour coefficient
directeur
a pour coefficient
directeur 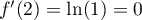 et passe par
et passe par 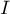 : c'est l'axe des
abscisses.
: c'est l'axe des
abscisses.
-
- Une équation de
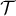 est:
est:
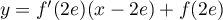 ,
avec
,
avec  et
et 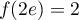 ,
d'où
,
d'où
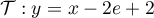 .
.
On a alors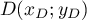 avec
avec 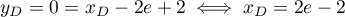 .
Ainsi,
.
Ainsi, 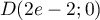 .
.
- L'aire de
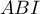 , trangle rectangle en
, trangle rectangle en 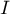 , est
, est

et l'aire du trapèze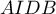 est
est
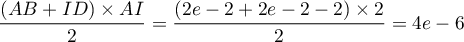 .
.
Ainsi le volume de la cuve est tel que
de la cuve est tel que
![\[5e\leqslant V\leqslant 5(4e-6)\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/39.png)
soit approximativement
![\[17,18\leqslant V\leqslant 24,37\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/40.png)
- Une équation de
-
- On a
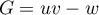 avec
avec 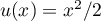 , donc
, donc 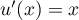 ,
,
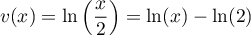 , donc
, donc 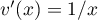 ,
et
,
et 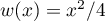 , donc
, donc 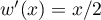 .
.
On a alors,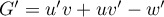 ,
soit
,
soit
![\[\begin{array}{ll}
G'(x)&=x\ln\lp\dfrac{x}2\rp+\dfrac{x^2}{2}\tm\dfrac1x-\dfrac{x}{2}\\[1em]
&=x\ln\lp\dfrac{x}{2}\rp+\dfrac{x}{2}-\dfrac{x}{2}\\[.8em]
&=g(x)\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/49.png)
ce qui montre que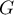 est bien une primitive de
est bien une primitive de 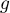 .
.
- On en déduit qu'une primitive de
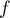 définie par
définie par
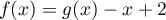 est donnée par
est donnée par
![\[F(x)=G(x)-\dfrac12x^2+2x\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/54.png)
- On peut alors calculer l'intégrale:
![\[\begin{array}{ll}
S&\dsp=\int_2^{2e}\Bigl(2-f(x)\Bigr)dx\\[1em]
&=\Bigl[ 2x-F(x)\Bigr]_2^{2e}\\[1em]
&=\Bigl[ -G(x)+\dfrac12x^2\Bigr]_2^{2e}\\[1em]
&=-G(2e)+\dfrac12(2e)^2-\Bigl(-G(2)+\dfrac122^2\Bigr)\\[.7em]
&=G(2)-G(2e)+2e^2-2
\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/55.png)
avec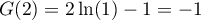 ,
et
,
et 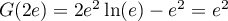 ,
donc
,
donc
![\[S=-1-e^2+2e^2-2=e^2-3\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/58.png)
et on en déduit le volume de la cuve: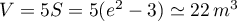 .
.
- On a
Partie B
- Le volume est
 avec
avec 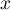 tel que
tel que 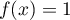 .
On cherche donc à résoudre l'équation
.
On cherche donc à résoudre l'équation  ,
avec
,
avec 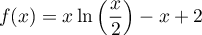 .
.
On ne sait pas résoudre excactement cette équation. On peut par contre le faire de manière approchée, en utilisant le théorème des valeurs intermédiaires.
On sait que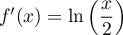 , d'après A.1.
et donc, comme
, d'après A.1.
et donc, comme 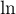 est strictement croissante sur
est strictement croissante sur 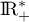 ,
que pour tout
,
que pour tout ![$x\in[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/68.png) ,
,
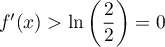 .
.
Ainsi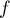 est strictement croissante sur
est strictement croissante sur ![$[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/71.png) , avec de plus
, avec de plus
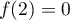 et
et 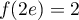 .
On en déduit, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
qu'il existe une unique solution
.
On en déduit, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
qu'il existe une unique solution ![$\alpha\in[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/74.png) à l'équation
à l'équation
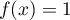 .
.
Avec la calculatrice (à l'aide d'un tableau de valeurs, ou par dichotomie par exemple), on trouve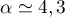 , et alors
le volume est de
, et alors
le volume est de 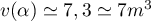 .
.
- Cet algorithme est un algorithme de recherche par dichotomie.
Il permet de chercher les valeurs d'un encadrement![$[a;b]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/78.png) pour lequel
la hauteur
pour lequel
la hauteur  correspond à la moitié de la cuve.
correspond à la moitié de la cuve.
Cet encadrement permet d'avoir un résultat précis à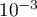 près.
près.
Cacher la correction
Exercice 4: Bac 2015: Skateparc: fonction avec logarithme, pentes, dérivées, primitive, intégrale, algorithme
![\psset{unit=0.3cm}
\begin{pspicture}(-1.5,-1.5)(29,19)
\psaxes[linewidth=1.pt,labels=none,tickstyle=bottom]{->}(0,0)(29,19)
\psplot[plotpoints=5000,linewidth=1.25pt]{0}{20}{x 1 add ln x 1 add mul 3 x mul sub 7 add}
\rput(7.07,7.07){\psplot[plotpoints=5000,linewidth=1.25pt]{0}{20}{x 1 add ln x 1 add mul 3 x mul sub 7 add}}
\pspolygon[showpoints](20,0)(27.07,7.07)(27.07,18.005)(20,10.935)%DD'C'C
\psline[showpoints](0,7.07)(7.07,14.14)%BB'
\psline[showpoints,linestyle=dashed](0,0)(7.07,7.07)(27.07,7.07)
\psline[linestyle=dashed,showpoints](7.07,7.07)(7.07,14.14)
\uput[dl](0,0){O} \uput[ul](7.07,7.07){A} \uput[l](0,7.07){B}
\uput[ul](7.07,14.14){B$'$} \uput[dr](20,10.935){C} \uput[dr](27.07,18.005){C$'$}
\uput[d](20,0){D} \uput[dr](27.07,7.07){D$'$} \uput[d](1,0){I}
\uput[l](0,1){J}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2015-Metropole-juin/1.png) |
Une municipalité a décidé d'installer un module de skateboard dans un parc de la commune.
Le dessin ci-contre en fournit une perspective cavalière. Les quadrilatères Le plan de face L'unité est le mètre. La largeur du module est de 10 mètres, autrement dit, |
Le but du problème est de déterminer l'aire des différentes surfaces à peindre.
Le profil du module de skateboard a été modélisé à partir d'une photo par la fonction
On note
Partie 1
|
![\psset{unit=0.3cm}
\begin{pspicture}(-1.5,-1.5)(23,13.5)
\psaxes[linewidth=1.25pt,labels=none,tickstyle=bottom]{->}(0,0)(23,13.5)
\psplot[plotpoints=5000,linewidth=1.25pt]{0}{20}{x 1 add ln x 1 add mul 3 x mul sub 7 add}
\uput[u](15,7){$\mathcal{C}$}\uput[d](20,0){D}\uput[l](0,7.07){B}\uput[dr](20,10.935){C}\uput[dl](0,0){O}\uput[d](1,0){I}
\uput[l](0,1){J}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2015-Metropole-juin/23.png) |
4. On admet que la fonction
a pour dérivée la fonction
Déterminer une primitive de la fonction
Partie 2
Les trois questions de cette partie sont indépendantes
- Les propositions suivantes sont-elles exactes ? Justifier les réponses.
- [
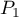 :] La différence de hauteur entre le point le plus haut et le point le plus bas de la piste est au moins égale à 8 mètres.
:] La différence de hauteur entre le point le plus haut et le point le plus bas de la piste est au moins égale à 8 mètres.
- [
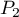 :] L'inclinaison de la piste est presque deux fois plus grande en
:] L'inclinaison de la piste est presque deux fois plus grande en 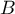 qu'en
qu'en 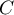 .
.
- [
- On souhaite recouvrir les quatre faces latérales de ce module d'une couche de peinture rouge. La peinture utilisée permet de couvrir une surface de
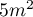 par litre.
par litre.
Déterminer, à 1 litre près, le nombre minimum de litres de peinture nécessaires.
-
On souhaite peindre en noir la piste roulante, autrement dit la surface supérieure du module.
Afin de déterminer une valeur approchée de l'aire de la partie à peindre, on considère dans le repère (O, I, J) du plan de face, les points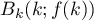 pour
pour  variant de 0 à 20.
variant de 0 à 20.
Ainsi,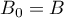 .
.
On décide d'approcher l'arc de la courbe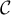 allant de
allant de 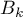 à
à 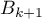 par le segment
par le segment ![$\left[B_kB_{k+1}\right]](/Generateur-Devoirs/TS/ChapIntegration/ex2015-Metropole-juin/43.png) .
.
Ainsi l'aire de la surface à peindre sera approchée par la somme des aires des rectangles du type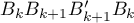 (voir figure).
(voir figure).
![\psset{xunit=0.3cm,yunit=0.35cm}
\begin{pspicture}(-2.2,-1.5)(29,17)
\psaxes[linewidth=1.25pt,labels=none,tickstyle=bottom]{->}(0,0)(29,19)
\psplot[plotpoints=5000,linewidth=1.25pt]{0}{20}{x 1 add ln x 1 add mul 3 x mul sub 7 add}
\rput(7.07,7.07){\psplot[plotpoints=5000,linewidth=1.25pt]{0}{20}{x 1 add ln x 1 add mul 3 x mul sub 7 add}}
\pspolygon(20,0)(27.07,7.07)(27.07,18.005)(20,10.935)%DD'C'C
\psline(0,7.07)(7.07,14.14)%BB'
\psline[linestyle=dashed](0,0)(7.07,7.07)(27.07,7.07)
\psline[linestyle=dashed](7.07,7.07)(7.07,14.14)
\uput[dl](0,0){O} \uput[ul](7.07,7.07){\scriptsize A} \uput[l](0,7.07){\scriptsize B}
\uput[ul](7.07,14.14){\scriptsize B$'$} \uput[dr](20,10.935){\footnotesize C} \uput[dr](27.07,18.005){\footnotesize C$'$}
\uput[d](20,0){\scriptsize D} \uput[dr](27.07,7.07){\scriptsize D$'$} \uput[d](1,0){\scriptsize I}
\psline[linestyle=dotted](1,5.39)(8.07,12.46)\uput[d](1,5.48){\scriptsize $B_1$}\uput[ur](8.07,12.46){\footnotesize $B'_1$}
\psline[linestyle=dotted](2,4.3)(9.07,11.37) \uput[d](2,4.34){\scriptsize $B_2$}\uput[ur](9.07,11.37){\footnotesize $B'_2$}
\psline[linestyle=dotted](7,2.64)(14.07,9.71)\uput[dl](7,2.64){\scriptsize $B_k$}\uput[ul](14.07,9.71){\footnotesize $B'_k$}
\psline[linestyle=dotted](8,2.78)(15.07,9.85)\uput[d](9,3.03){\scriptsize $B_{k+1}$}\uput[u](16.07,10.1){\scriptsize $B'_{k+1}$}
\uput[l](0,1){J}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2015-Metropole-juin/45.png)
- Montrer que pour tout entier
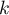 variant de 0 à 19,
variant de 0 à 19,
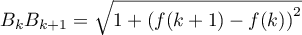 .
.
- Compléter l'algorithme suivant pour qu'il affiche une estimation de l'aire de la partie roulante.
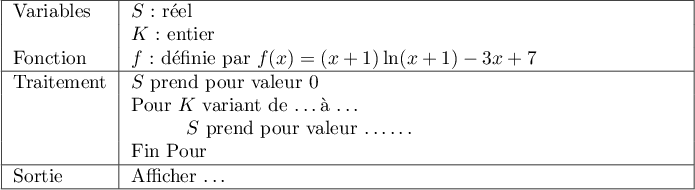
- Montrer que pour tout entier
Correction exercice 4
Partie 1
-
 avec
avec 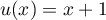 , donc
, donc 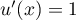 ,
,
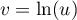 , donc
, donc  soit
soit 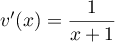 et
et 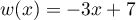 donc
donc 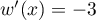 .
.
On a alors ,
soit
,
soit 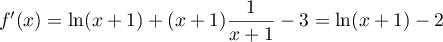 .
.
-
 , par croissance de la
fonction exponentielle, et donc
, par croissance de la
fonction exponentielle, et donc 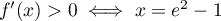 .
.
![\begin{tabular}{|c|ccccc|}\hline
x&0&&$e^{2}-1$&&20\\\hline
$f'(x)$&&-&\zb&+&\\\hline
&7&&&&$f(20)\simeq 10,93$\\
$f(x)$&&\psline[arrowsize=7pt]{->}(-.4,.4)(.6,-.5)&&
\psline[arrowsize=7pt]{->}(-.6,-.5)(.4,.4)&\\
&&&$\begin{array}{c}f\left( e^{2}-1\rp\\=10-e^2\simeq 2,6\enar$&&\\\hline
\end{tabular}](/Generateur-Devoirs/TS/ChapIntegration/ex2015-Metropole-juin_c/13.png)
- Le coefficient directeur de la tangente à
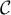 au point d'abscisse
au point d'abscisse 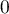 est
est  .
.
- Une primitive de
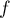 est donc donnée par
est donc donnée par
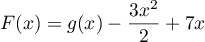
Partie 2
-
- La différence entre les points le plus haut et le plus bas est
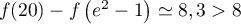 donc
donc 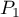 est vraie.
est vraie.
-
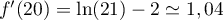 . D'après la question 3.,
l'inclinaison en
. D'après la question 3.,
l'inclinaison en  est 2, donc
est 2, donc  est vraie.
est vraie.
- La différence entre les points le plus haut et le plus bas est
- L'aire de la face avant, en unités d'aire, vaut
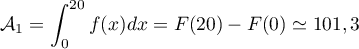 .
.
L'aire latérale gauche vaut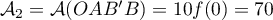 .
.
L'aire latérale droite vaut .
.
L'aire à peindre est donc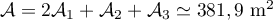 .
.
Il faut prévoir donc au minimum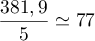 litres de peinture.
litres de peinture.
-
-
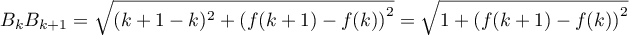 .
.
- La partie de l'algorithme à compléter est :
 prend la valeur 0.
prend la valeur 0.
Pour allant de 0 à 19
allant de 0 à 19
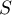 prend la valeur
prend la valeur 
Fin Pour
-
Cacher la correction
Exercice 5: Bac 2014: Exponentielle et (un peu pour finir d') intégrales
Sur le graphique ci-dessous, on a tracé, dans un repère orthonormé
 , une courbe
, une courbe  et la droite
et la droite 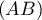 où
où 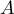 et
et 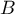 sont les points de coordonnées respectives
sont les points de coordonnées respectives 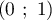 et
et
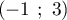 .
.
![\psset{unit=1.2cm,arrowsize=7pt}
\begin{pspicture}(-3,-2.2)(3,3.5)
\psline[linewidth=1pt]{->}(-3,0)(3,0)
\psline[linewidth=1pt]{->}(0,-2.2)(0,3.8)
\rput(0,1){$\tm$}\rput(-1,3){$\tm$}
\uput[ur](0,1){$A$}\uput[l](-1,3){$B$}
\uput[dl](0,0){O}
\psline[linewidth=1.6pt]{->}(0,0)(1,0)\uput[d](0.5,0){$\vec{i}$}
\uput[d](-1,0){$- 1$}\uput[r](0,3){3}
\psline[linewidth=1.6pt]{->}(0,0)(0,1)\uput[l](0,0.5){$\vec{j}$}
\uput[d](-2,-1.2){$\mathcal{C}$}
\psline[linestyle=dashed](-1,0)(-1,3)(0,3)
\psplot[plotpoints=5000,linewidth=1.25pt,linecolor=blue]{-2.5}{2.5}{1 x add x 3 mul 2.71828 x dup mul exp div sub}
\psplot{-1.4}{1.5}{1 x 2 mul sub}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/8.png)
On désigne par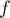 la fonction dérivable sur
la fonction dérivable sur 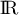 dont la courbe
représentative est
dont la courbe
représentative est 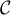 .
.
On suppose, de plus, qu'il existe un réel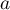 tel que pour tout réel
tel que pour tout réel 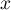 ,
,
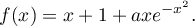
Bac S - métropole, 11 septembre 2014 - 5 points
Cacher la correction
![\psset{unit=1.2cm,arrowsize=7pt}
\begin{pspicture}(-3,-2.2)(3,3.5)
\psline[linewidth=1pt]{->}(-3,0)(3,0)
\psline[linewidth=1pt]{->}(0,-2.2)(0,3.8)
\rput(0,1){$\tm$}\rput(-1,3){$\tm$}
\uput[ur](0,1){$A$}\uput[l](-1,3){$B$}
\uput[dl](0,0){O}
\psline[linewidth=1.6pt]{->}(0,0)(1,0)\uput[d](0.5,0){$\vec{i}$}
\uput[d](-1,0){$- 1$}\uput[r](0,3){3}
\psline[linewidth=1.6pt]{->}(0,0)(0,1)\uput[l](0,0.5){$\vec{j}$}
\uput[d](-2,-1.2){$\mathcal{C}$}
\psline[linestyle=dashed](-1,0)(-1,3)(0,3)
\psplot[plotpoints=5000,linewidth=1.25pt,linecolor=blue]{-2.5}{2.5}{1 x add x 3 mul 2.71828 x dup mul exp div sub}
\psplot{-1.4}{1.5}{1 x 2 mul sub}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/8.png)
On désigne par
On suppose, de plus, qu'il existe un réel
-
- Justifier que la courbe
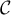 passe par le point
passe par le point 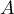 .
.
- Déterminer le coefficient directeur de la droite
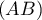 .
.
- Démontrer que pour tout réel
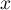 ,
,
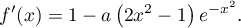
- On suppose que la droite
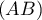 est tangente à la courbe
est tangente à la courbe
 au point
au point  .
.
Déterminer la valeur du réel .
.
- Justifier que la courbe
- D'après la question précédente, pour tout réel
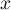 ,
,
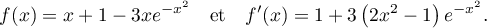
- Démontrer que pour tout réel
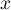 de l'intervalle
de l'intervalle
![$]- 1~;~0]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/27.png) ,
,  .
.
- Démontrer que pour tout réel
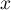 inférieur ou égal à
inférieur ou égal à 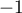 ,
,
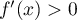 .
.
- Démontrer qu'il existe un unique réel
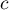 de l'intervalle
de l'intervalle
![$\left[- \dfrac{3}{2}~;~- 1\right]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/33.png) tel que
tel que 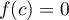 .
Justifier que
.
Justifier que 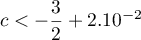 .
.
- Démontrer que pour tout réel
- On désigne par
 l'aire, exprimée en unités d'aire,
du domaine défini par:
l'aire, exprimée en unités d'aire,
du domaine défini par:
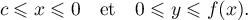
- Écrire
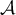 sous la forme d'une intégrale.
sous la forme d'une intégrale.
- On admet que l'intégrale
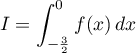 est une valeur approchée de
est une valeur approchée de 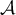 à
à 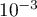 près.
près.
Calculer la valeur exacte de l'intégrale .
.
- Écrire
Correction exercice 5
Bac S - métropole, 11 septembre 2014 - 5 points
-
- On a
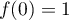 ce qui montre que le point de coordonnées
ce qui montre que le point de coordonnées
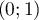 , c'est-à-dire
, c'est-à-dire 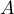 , appartient à
, appartient à 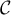 .
.
- Le coefficient directeur de la droite
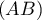 est
est
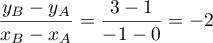 .
.
-
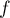 est de la forme
est de la forme
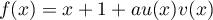 ,
avec
,
avec 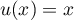 donc
donc 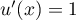 et
et 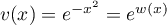 donc
donc 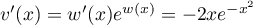 .
.
Ainsi,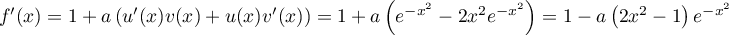 .
.
- Si la droite
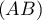 est tangente à la courbe
est tangente à la courbe 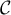 au
point
au
point  d'abscisse
d'abscisse  , alors le coefficient directeur de
, alors le coefficient directeur de 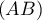 est
est 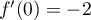 .
Ainsi,
.
Ainsi, 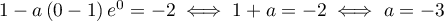
- On a
- On a donc, avec
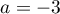 ,
,
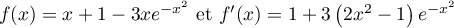 .
.
- Pour tout réel
![$x\in]-1;0]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole_c/23.png) ,
, 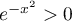 et
et
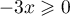 , donc
, donc 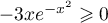 .
.
Pour tout![$x\in]-1;0]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole_c/27.png) ,
, 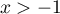 , donc
, donc 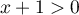 ,
alors, par addition,
,
alors, par addition, 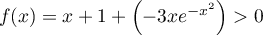 .
.
- Pour
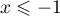 ,
, 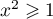 ,
donc,
,
donc, 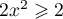 et
et 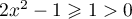 .
Ainsi,
.
Ainsi, 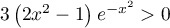 et alors
et alors
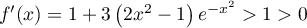 .
.
- Sur
![$] -\infty\,;\,-1]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole_c/37.png) ,
, 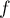 est dérivable donc continue,
avec
est dérivable donc continue,
avec 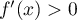 donc la fonction
donc la fonction 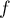 est
strictement croissante sur cet intervalle donc aussi sur l'intervalle
est
strictement croissante sur cet intervalle donc aussi sur l'intervalle
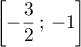 .
.
Or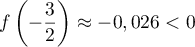 et
et 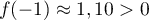 donc, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
l'équation
donc, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
l'équation 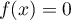 admet une solution unique
admet une solution unique 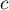 dans l'intervalle
dans l'intervalle
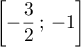 .
.
Or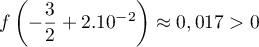 donc
donc 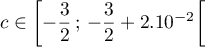 et donc
et donc 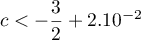 .
.
- Pour tout réel
-
- Comme
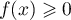 sur
sur ![$[c;0]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole_c/51.png) ,
alors
,
alors 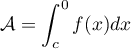 .
.
- La fonction
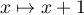 a pour primitive la fonction
a pour primitive la fonction
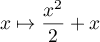 .
.
La fonction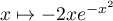 (forme
(forme 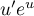 ) a pour
primitive la fonction
) a pour
primitive la fonction 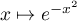 donc la fonction
donc la fonction 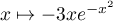 a pour primitive la fonction
a pour primitive la fonction
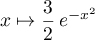 .
.
La fonction a donc pour primitive la fonction
a donc pour primitive la fonction  définie par
définie par 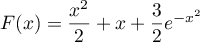 .
.
On a alors
- Comme
Cacher la correction
Exercice 6: Bac 2014: Suite d'intégrales et exponentielle
Bac S, 19 juin 2014, 5 points
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par la courbe représentative de la fonction
la courbe représentative de la fonction  définie sur
définie sur  par:
par:
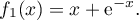
Partie B
L'objet de cette partie est d'étudier la suite définie sur
définie sur  par:
par:
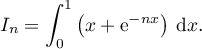
Partie A
Partie B
Cacher la correction
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par
- Justifier que
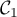 passe par le point A de coordonnées
passe par le point A de coordonnées  .
.
- Déterminer le tableau de variation de la fonction
 . On
précisera les limites de
. On
précisera les limites de 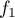 en
en  et en
et en  .
.
Partie B
L'objet de cette partie est d'étudier la suite
- Dans le plan muni d'un repère orthonormé
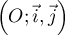 ,
pour tout entier
naturel
,
pour tout entier
naturel 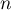 , on note
, on note 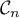 la courbe représentative de la
fonction
la courbe représentative de la
fonction 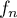 définie sur
définie sur 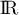 par
par
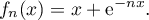
Sur le graphique ci-dessous on a tracé la courbe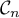 pour plusieurs valeurs de l'entier
pour plusieurs valeurs de l'entier 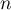 et la droite
et la droite 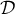 d'équation
d'équation 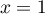 .
.
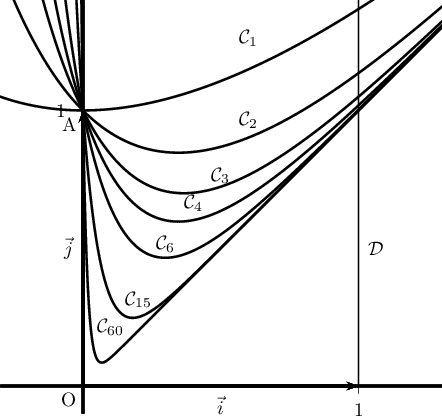
- Interpréter géométriquement l'intégrale
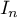 .
.
- En utilisant cette interprétation, formuler une conjecture sur
le sens de variation de la suite
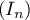 et sa limite
éventuelle. On précisera les éléments sur lesquels on s'appuie
pour conjecturer.
et sa limite
éventuelle. On précisera les éléments sur lesquels on s'appuie
pour conjecturer.
- Interpréter géométriquement l'intégrale
- Démontrer que pour tout entier naturel
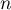 supérieur ou égal à 1,
supérieur ou égal à 1,
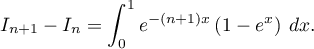
En déduire le signe de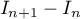 puis démontrer que la suite
puis démontrer que la suite
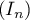 est convergente.
est convergente.
- Déterminer l'expression de
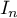 en fonction de
en fonction de 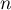 et
déterminer la limite de la suite
et
déterminer la limite de la suite 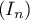 .
.
Correction exercice 6
Partie A
- On a
 et donc
et donc  .
.
- Comme
 et
et  sont définies et dérivables
sur
sont définies et dérivables
sur  ,
,  est aussi définie et dérivable sur
est aussi définie et dérivable sur  , comme somme
et composéee de fonctions définies et dérivables sur
, comme somme
et composéee de fonctions définies et dérivables sur  ,
avec,
pout tout
,
avec,
pout tout  ,
,  .
.
De plus, ,
car la fonction exponentielle est strictement croissante sur
,
car la fonction exponentielle est strictement croissante sur  ,
et ainsi,
,
et ainsi,  .
.
En ,
,  et
et
 , et donc,
par somme des limites,
, et donc,
par somme des limites,  .
.
En ,
,
 , avec
, avec
 et
et
 (croissance comparée en l'infini de
l'exponentielle et des polynômes).
(croissance comparée en l'infini de
l'exponentielle et des polynômes).
Ainsi, , et alors, par
produit des limites,
, et alors, par
produit des limites,
 .
.

Partie B
-
-
 est l'aire sous la courbe
est l'aire sous la courbe  :
l'aire du domaine compris entre les droites verticales
d'équation
:
l'aire du domaine compris entre les droites verticales
d'équation  et
et  , et entre l'axe des abscisses et la
courbe
, et entre l'axe des abscisses et la
courbe  .
.
- Il semblerait que la courbe
 soit en
dessous de la courbe
soit en
dessous de la courbe  .
On peut donc conjecturer que la suite
.
On peut donc conjecturer que la suite  est décroissante.
est décroissante.
Il semblerait de plus que lorsque devient grand, la courbe
devient grand, la courbe
 se rapproche de la diagonale du carré de côté
se rapproche de la diagonale du carré de côté
 .
On peut ainsi conjecturer que la suite
.
On peut ainsi conjecturer que la suite  est
convergente, de limite
est
convergente, de limite  .
.
-
- Pour tout entier
 ,
,

car .
.
De plus, pour tout ,
,
 ,
et
,
et  , car la fonction exponentielle est strictement
croissante sur
, car la fonction exponentielle est strictement
croissante sur  , et donc,
, et donc,  .
.
On en déduit que pour tout ,
,
 ,
et donc que
,
et donc que

Ainsi, la suite est décroissante.
est décroissante.
Comme pour tout et pour tout entier
et pour tout entier  ,
,
 , et donc,
, et donc,  ,
on a
,
on a  .
.
Ainsi, est une suite décroissante et minorée par 0:
est une suite décroissante et minorée par 0:
 est donc convergente.
est donc convergente.
- Pour tout entier
 ,
,

Comme et
et  ,
on a donc,
,
on a donc,
 ,
ce qui démontre la conjecture émise au début de cette partie.
,
ce qui démontre la conjecture émise au début de cette partie.
Cacher la correction
Exercice 7: Bac 2008: Calcul d'une aire entre deux courbes de logarithmes
Les courbes C et C' données ci-dessous représentent respectivement, dans un repère orthonormal 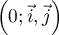 , les fonctions
, les fonctions 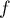 et
et 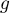 définies sur l'intervalle
définies sur l'intervalle ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/4.png) par
par 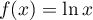 et
et 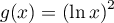 .
.
![\[\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-3.2)(4,3.2)
\newcommand{\f}[1]{x ln}
\newcommand{\g}[1]{x ln 2 exp}
\pscustom{
\psplot{1}{2.718}{\f{x}} \gsave
\psplot{2.718}{1}{\g{x}}
\fill[fillstyle=solid,fillcolor=lightgray]
%\fill[fillstyle=vlines]
\grestore}
\psline(-.2,0)(4,0)
\psline(0,-3)(0,3)
\multido{\i=1+1}{4}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\multido{\i=-3+1}{7}{\psline(-.1,\i)(.1,\i)\rput[r](-.1,\i){\i}}
\psplot{.05}{4}{\f{x}}
\psplot{.1}{4}{\g{x}}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/7.png)
Bac juin 2008
Cacher la correction
![\[\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-3.2)(4,3.2)
\newcommand{\f}[1]{x ln}
\newcommand{\g}[1]{x ln 2 exp}
\pscustom{
\psplot{1}{2.718}{\f{x}} \gsave
\psplot{2.718}{1}{\g{x}}
\fill[fillstyle=solid,fillcolor=lightgray]
%\fill[fillstyle=vlines]
\grestore}
\psline(-.2,0)(4,0)
\psline(0,-3)(0,3)
\multido{\i=1+1}{4}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\multido{\i=-3+1}{7}{\psline(-.1,\i)(.1,\i)\rput[r](-.1,\i){\i}}
\psplot{.05}{4}{\f{x}}
\psplot{.1}{4}{\g{x}}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/7.png)
- On cherche à déterminer l'aire A (en unités d'aire) de la partie grisée.
On note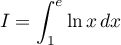 et
et 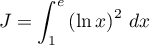 .
.
- Vérifier que la fonction
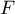 définie sur l'intervalle
définie sur l'intervalle ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/11.png) par
par
 est une primitive de la fonction logarithme népérien.
En déduire
est une primitive de la fonction logarithme népérien.
En déduire  .
.
- Démontrer à l'aide d'une intégration par partie que
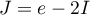 .
.
- Donner la valeur de A.
- Vérifier que la fonction
- Pour
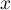 appartenant à l'intervalle
appartenant à l'intervalle ![$[1;e]$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/16.png) , on note
, on note 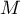 le point de la courbe C d'abscisse
le point de la courbe C d'abscisse 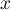 et
et  le point de la courbe C' de même abscisse.
le point de la courbe C' de même abscisse.
Pour quelle valeur de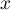 la distance MN est-elle maxiale ?
Calculer la valeur maximale de MN.
la distance MN est-elle maxiale ?
Calculer la valeur maximale de MN.
Correction exercice 7
Bac juin 2008
-
- On dérive:
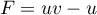 avec
avec 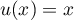 donc
donc  et
et 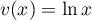 donc
donc  ,
,
et alors,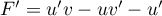 ,
,
soit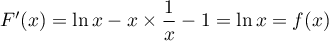
ce qui montre que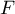 est bien une primtive de
est bien une primtive de 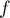 .
.
On en déduit
![\[\begin{array}{ll}I&=\dsp\int_1^e\ln x\,dx
=\Bigl[\,F(x)\,\Bigr]_1^e
=F(e)-F(1)\\[1em]
&=\left( e\ln e-e\rp-\left( 1\ln 1-1\rp
=1\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/10.png)
- On pose
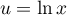 donc
donc 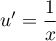 et
et 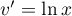 donc
donc 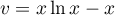 et et alors, en intégrant par parties,
et et alors, en intégrant par parties,
![\[\begin{array}{ll}J&=\Bigl[\ln x\left( x\ln x-x\rp\Bigr]_1^e
-\dsp\int_1^e\dfrac1x\left( x\ln x-x\rp\\[1em]
&=0-\dsp\int_1^e\lp\ln x-1\rp\,dx\\[1em]
&=-\dsp\int_1^e\ln x\,dx+\int_1^e1dx\\[1em]
&=-I+e-1=e-2I\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/15.png)
car .
.
- On en déduit la valeur de A:
![\[\begin{array}{ll}A&=\dsp\int_1^e\left( f(x)-g(x)\rp\,dx\\[1em]
&=\dsp\int_1^ef(x)\,dx-\int_1^eg(x)\,dx\\[1em]
&=I-J
=1-\left( e-2I\rp\\
&=1-\left( e-2\rp=3-e\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/17.png)
- On dérive:
- Pour
![$x\in[1;e]$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/18.png) , on a
, on a
![\[\begin{array}{ll}MN&=d(x)=f(x)-g(x)\\[.5em]&=\ln x-\lp\ln x\rp^2\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/19.png)
Pour trouver le maximum de cette fonction, il suffit de connaître ses variations.
On a
![\[d'(x)=\dfrac1x-2\dfrac1x\ln x=\dfrac1x\lp1-2\ln x\rp\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/20.png)
avec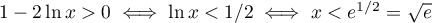 et donc
et donc
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ &$1$ && $\sqrt{e}$ && $e$\\\hline
$1/x$ && $+$ &$|$&$+$&\\\hline
$1-2\ln x$ && $+$ &\zb&$-$&\\\hline
$d'(x)$ && $+$ &\zb&$-$&\\\hline
&&&$d\lp\sqrt{e}\rp$&&\\
$d$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/22.png)
La distance est donc maximale en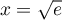 et cette distance maximale est
et cette distance maximale est
![\[d\lp\sqrt{e}\rp=\ln\sqrt{e}-\lp\ln\sqrt{e}\rp^2
=\dfrac12-\lp\dfrac12\rp^2=\dfrac14\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/24.png)
Cacher la correction
Quelques autres devoirs
intégration, Calculs d'intégrales - Suite d'intégrales (Bac S, 19 juin 2014) - Dimensionnement d'un récupérateur d'eau (Bac S - Amérique du nord, 1er juin 2016)
intégration, Calculs d'intégrales - Aire sous une courbe (Bac S - métropole, 11 septembre 2014) - Aire entre deux courbes (Bac S, juin 2008)
sur les intégrales: calcul d'intégrales, suite d'intégrales, et un calcul de volume
sur les intégrales: calcul d'intégrales, suite d'intégrales
Quelques exercices corrigés
Exercices corrigés
Bac 2014 (Antilles-Guyane) - Étude de fonctions, limites, TVI, tangente, intégrale
Exercices corrigés
Bac 2024 (19 juin): Logarithme, variation, limites et TVI, convexité et intégrale
Exercices corrigés
Bac 2013 - Fonction avec log, dérivée, limites, TVI, algorithme, intégrale
Exercices corrigés
Calculs d'intégrales
Exercices corrigés
Calculs d'intégrales (bis)
Voir aussi: