Devoir de maths corrigé, Intégrales
Terminale générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, posé en spé maths, terminale générale, année scolaire 2022/2023
Exercice 1: Quelques calculs d'intégrales
Calculer les intégrales:
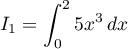 ;
;
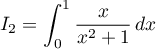 ;
;
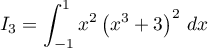
À l'aide d'une intégration par parties, calculer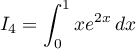
À l'aide d'une intégration par parties, calculer
Exercice 2: Suite d'intégrales et exponentielle
Bac S, 19 juin 2014, 5 points
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par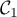 la courbe représentative de la fonction
la courbe représentative de la fonction 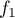 définie sur
définie sur  par:
par:
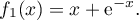
Partie B
L'objet de cette partie est d'étudier la suite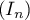 définie sur
définie sur  par:
par:
Partie A
Partie B
Cacher la correction
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par
- Justifier que
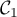 passe par le point A de coordonnées
passe par le point A de coordonnées 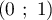 .
.
- Déterminer le tableau de variation de la fonction
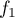 . On
précisera les limites de
. On
précisera les limites de 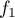 en
en 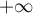 et en
et en 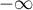 .
.
Partie B
L'objet de cette partie est d'étudier la suite
- Dans le plan muni d'un repère orthonormé
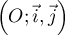 ,
pour tout entier
naturel
,
pour tout entier
naturel 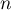 , on note
, on note 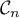 la courbe représentative de la
fonction
la courbe représentative de la
fonction 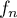 définie sur
définie sur 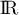 par
par
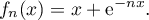
Sur le graphique ci-dessous on a tracé la courbe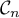 pour plusieurs valeurs de l'entier
pour plusieurs valeurs de l'entier 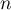 et la droite
et la droite 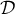 d'équation
d'équation 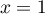 .
.
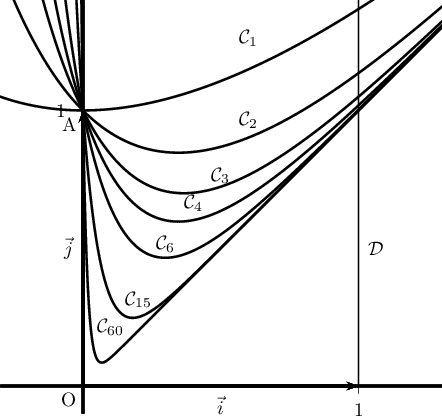
- Interpréter géométriquement l'intégrale
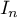 .
.
- En utilisant cette interprétation, formuler une conjecture sur
le sens de variation de la suite
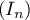 et sa limite
éventuelle. On précisera les éléments sur lesquels on s'appuie
pour conjecturer.
et sa limite
éventuelle. On précisera les éléments sur lesquels on s'appuie
pour conjecturer.
- Interpréter géométriquement l'intégrale
- Démontrer que pour tout entier naturel
 supérieur ou égal à 1,
supérieur ou égal à 1,
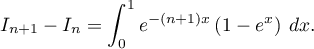
En déduire le signe de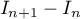 puis démontrer que la suite
puis démontrer que la suite
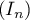 est convergente.
est convergente.
- Déterminer l'expression de
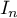 en fonction de
en fonction de 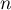 et
déterminer la limite de la suite
et
déterminer la limite de la suite 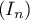 .
.
Correction exercice 2
Partie A
- On a
 et donc
et donc  .
.
- Comme
 et
et  sont définies et dérivables
sur
sont définies et dérivables
sur  ,
,  est aussi définie et dérivable sur
est aussi définie et dérivable sur  , comme somme
et composéee de fonctions définies et dérivables sur
, comme somme
et composéee de fonctions définies et dérivables sur  ,
avec,
pout tout
,
avec,
pout tout  ,
,  .
.
De plus, ,
car la fonction exponentielle est strictement croissante sur
,
car la fonction exponentielle est strictement croissante sur  ,
et ainsi,
,
et ainsi,  .
.
En ,
,  et
et
 , et donc,
par somme des limites,
, et donc,
par somme des limites,  .
.
En ,
,
 , avec
, avec
 et
et
 (croissance comparée en l'infini de
l'exponentielle et des polynômes).
(croissance comparée en l'infini de
l'exponentielle et des polynômes).
Ainsi, , et alors, par
produit des limites,
, et alors, par
produit des limites,
 .
.

Partie B
-
-
 est l'aire sous la courbe
est l'aire sous la courbe  :
l'aire du domaine compris entre les droites verticales
d'équation
:
l'aire du domaine compris entre les droites verticales
d'équation  et
et  , et entre l'axe des abscisses et la
courbe
, et entre l'axe des abscisses et la
courbe  .
.
- Il semblerait que la courbe
 soit en
dessous de la courbe
soit en
dessous de la courbe  .
On peut donc conjecturer que la suite
.
On peut donc conjecturer que la suite  est décroissante.
est décroissante.
Il semblerait de plus que lorsque devient grand, la courbe
devient grand, la courbe
 se rapproche de la diagonale du carré de côté
se rapproche de la diagonale du carré de côté
 .
On peut ainsi conjecturer que la suite
.
On peut ainsi conjecturer que la suite  est
convergente, de limite
est
convergente, de limite  .
.
-
- Pour tout entier
 ,
,

car .
.
De plus, pour tout ,
,
 ,
et
,
et  , car la fonction exponentielle est strictement
croissante sur
, car la fonction exponentielle est strictement
croissante sur  , et donc,
, et donc,  .
.
On en déduit que pour tout ,
,
 ,
et donc que
,
et donc que

Ainsi, la suite est décroissante.
est décroissante.
Comme pour tout et pour tout entier
et pour tout entier  ,
,
 , et donc,
, et donc,  ,
on a
,
on a  .
.
Ainsi, est une suite décroissante et minorée par 0:
est une suite décroissante et minorée par 0:
 est donc convergente.
est donc convergente.
- Pour tout entier
 ,
,

Comme et
et  ,
on a donc,
,
on a donc,
 ,
ce qui démontre la conjecture émise au début de cette partie.
,
ce qui démontre la conjecture émise au début de cette partie.
Cacher la correction
Exercice 3: Récupérateur d'eau (Bac 2016)
Un particulier veut faire fabriquer un récupérateur d'eau.
Ce récupérateur d'eau est une cuve qui doit respecter le cahier des
charges suivant:
Cette cuve est schématisée ci-dessous.
![$$(-1.8,-0.5)(7,5)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\pspolygon(2,0)(2,1.8)(-1.3,2.5)(-1.3,0.7)
\rput(-3.3,0.7){\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}}
\psline(2.1,2.7)(5.4,2)
\psline(-1.3,2.5)(2.1,2.7)
\psline(2,1.8)(5.4,2)
\psline[linewidth=0.5pt](2,1.8)(2,3)\psline[linewidth=0.5pt](-1.3,2.5)(-1.3,3.7)
\psset{arrowsize=2pt 3}
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(2,3)(-1.3,3.7)
\psline[linewidth=0.5pt](2,1.8)(1.2,1.75)\psline[linewidth=0.5pt](2,0)(1.2,-0.05)
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(1.2,1.75)(1.2,-0.05)
\uput[l](1.2,0.85){2 m}\uput[u](1.35,3.35){5 m}
$$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/1.png)
La partie incurvée est modélisée par la courbe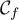 de la
fonction
de la
fonction 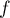 sur l'intervalle
sur l'intervalle ![$[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/4.png) définie par:
définie par:
![\[f(x)=x\ln \lp\dfrac{x}{2}\rp-x+2.\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/5.png)
La courbe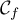 est représentée ci-dessous dans un repère
orthonormé d'unité 1m et constitue une vue de profil de la cuve.
est représentée ci-dessous dans un repère
orthonormé d'unité 1m et constitue une vue de profil de la cuve.
On considère les points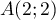 ,
, 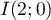 et
et 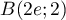 .
.
(-0.2,-0.25)(6,2.5)
\psaxes[linewidth=1.25pt](0,0)(0,0)(6,2.5)
\uput[u](2.8,0.2){$\mathcal{C}_f$}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\psframe[fillstyle=solid,fillcolor=lightgray](2,2)
\psdots(2,2)(5.437,2)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psplot[plotpoints=4000]{3}{5.8}{x 2 add 5.437 sub}
\uput[u](2,2){$A$}
\uput[u](5.437,2){$B$}
\uput[ul](5.75,2.2){$\mathcal{T}$}
\uput[dl](2,0){$I$}
\uput[dr](3.437,0){$D$}
\rput(1,1){Terrain}
\rput(3.2,1.2){Cuve}
\rput(4.7,0.5){Terrain}
\psline[linestyle=dotted,linewidth=1.5pt](2,2)(5.437,2)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/10.png)
Partie A L'objectif de cette partie est d'évaluer le volume de la cuve.
Partie B Pour tout réel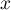 compris
entre
compris
entre 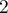 et
et 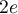 , on note
, on note 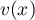 le volume d'eau, exprimé en m3, se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est
égale à
le volume d'eau, exprimé en m3, se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est
égale à 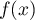 .
.
On admet que, pour tout réel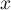 de l'intervalle [2 ; 2e],
de l'intervalle [2 ; 2e],
![\[v(x) = 5\left[\dfrac{x^2}{2}\ln \left( \dfrac{x}{2}\right) - 2x\ln\left( \dfrac{x}{2}\right) - \dfrac{x^2}{4} + 2x - 3\right].\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/49.png)
{\n}}
}
\pspolygon[fillstyle=solid,fillcolor=gray](2,0.1)(2,1.5)(0.35,2.3)(0.35,0.9)
\pspolygon[fillstyle=solid,fillcolor=gray](2,1.5)(0.35,2.3)(3.37,2.47)(5.08,1.7)
\pscustom[fillstyle=solid,fillcolor=gray]{
\pscurve(2,0.1)(3,0.316)(4,0.87)(5.08,1.75)
\psline(5.08,1.75)(2,1.5)
}
\pspolygon(5.437,2.1)(2,1.85)(0.35,2.7)(3.787,2.95)
\psline(2,1.85)(2,1.5)
\psline(0.35,2.7)(0.35,2.3)
\pscurve(0.35,0.9)(1.35,1.16)(2.35,1.72)(3.35,2.5)(3.787,2.95)
\psline[linestyle=dotted,linewidth=1.5pt](5.08,0.2)(5.08,1.75)(0,1.37)
\uput[d](5.2,0.3){$x$}
\uput[l](0,1.37){$f(x)$}
\multido{\n=0+1}{4}{\uput[l](0,\n){\n}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/50.png)
Bac S - Amérique du nord, 1er juin 2016 6 points
Partie A
Partie B
Cacher la correction
- elle doit être située à deux mètres de sa maison;
- la profondeur maximale doit être de deux mètres;
- elle doit mesurer cinq mètres de long;
- elle doit épouser la pente naturelle du terrain.
Cette cuve est schématisée ci-dessous.
![$$(-1.8,-0.5)(7,5)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\pspolygon(2,0)(2,1.8)(-1.3,2.5)(-1.3,0.7)
\rput(-3.3,0.7){\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}}
\psline(2.1,2.7)(5.4,2)
\psline(-1.3,2.5)(2.1,2.7)
\psline(2,1.8)(5.4,2)
\psline[linewidth=0.5pt](2,1.8)(2,3)\psline[linewidth=0.5pt](-1.3,2.5)(-1.3,3.7)
\psset{arrowsize=2pt 3}
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(2,3)(-1.3,3.7)
\psline[linewidth=0.5pt](2,1.8)(1.2,1.75)\psline[linewidth=0.5pt](2,0)(1.2,-0.05)
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(1.2,1.75)(1.2,-0.05)
\uput[l](1.2,0.85){2 m}\uput[u](1.35,3.35){5 m}
$$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/1.png)
La partie incurvée est modélisée par la courbe
La courbe
On considère les points
(-0.2,-0.25)(6,2.5)
\psaxes[linewidth=1.25pt](0,0)(0,0)(6,2.5)
\uput[u](2.8,0.2){$\mathcal{C}_f$}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\psframe[fillstyle=solid,fillcolor=lightgray](2,2)
\psdots(2,2)(5.437,2)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psplot[plotpoints=4000]{3}{5.8}{x 2 add 5.437 sub}
\uput[u](2,2){$A$}
\uput[u](5.437,2){$B$}
\uput[ul](5.75,2.2){$\mathcal{T}$}
\uput[dl](2,0){$I$}
\uput[dr](3.437,0){$D$}
\rput(1,1){Terrain}
\rput(3.2,1.2){Cuve}
\rput(4.7,0.5){Terrain}
\psline[linestyle=dotted,linewidth=1.5pt](2,2)(5.437,2)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/10.png)
Partie A L'objectif de cette partie est d'évaluer le volume de la cuve.
- Justifier que les points
 et
et 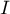 appartiennent à la courbe
appartiennent à la courbe
 et que l'axe des abscisses est tangent à la courbe
et que l'axe des abscisses est tangent à la courbe
 au point
au point 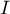 .
.
- On note
 la tangente à la courbe
la tangente à la courbe 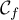 au
point
au
point  , et
, et 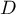 le point d'intersection de la droite
le point d'intersection de la droite 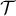 avec l'axe des abscisses.
avec l'axe des abscisses.
- Déterminer une équation de la droite
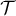 et en
déduire les coordonnées de
et en
déduire les coordonnées de  .
.
- On appelle
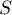 l'aire du domaine délimité par la courbe
l'aire du domaine délimité par la courbe
 , les droites d'équations
, les droites d'équations 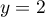 ,
,  et
et  .
.
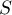 peut être encadrée par l'aire du triangle
peut être encadrée par l'aire du triangle 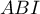 et celle du
trapèze
et celle du
trapèze  .
.
Quel encadrement du volume de la cuve peut-on en déduire ?
- Déterminer une équation de la droite
-
- Montrer que, sur l'intervalle
![$[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/31.png) ,
la fonction
,
la fonction 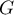 définie par
définie par
![\[G(x)=\dfrac{x^2}{2}\ln \lp\dfrac{x}{2}\rp-\dfrac{x^2}{4}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/33.png)
est une primitive de la fonction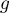 définie par
définie par
 .
.
- En déduire une primitive
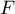 de la fonction
de la fonction 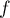 sur
l'intervalle
sur
l'intervalle ![$[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/38.png) .
.
- Déterminer la valeur exacte de l'aire
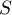 et en déduire une
valeur approchée du volume
et en déduire une
valeur approchée du volume 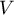 de la cuve au m3 près.
de la cuve au m3 près.
- Montrer que, sur l'intervalle
Partie B Pour tout réel
On admet que, pour tout réel
{\n}}
}
\pspolygon[fillstyle=solid,fillcolor=gray](2,0.1)(2,1.5)(0.35,2.3)(0.35,0.9)
\pspolygon[fillstyle=solid,fillcolor=gray](2,1.5)(0.35,2.3)(3.37,2.47)(5.08,1.7)
\pscustom[fillstyle=solid,fillcolor=gray]{
\pscurve(2,0.1)(3,0.316)(4,0.87)(5.08,1.75)
\psline(5.08,1.75)(2,1.5)
}
\pspolygon(5.437,2.1)(2,1.85)(0.35,2.7)(3.787,2.95)
\psline(2,1.85)(2,1.5)
\psline(0.35,2.7)(0.35,2.3)
\pscurve(0.35,0.9)(1.35,1.16)(2.35,1.72)(3.35,2.5)(3.787,2.95)
\psline[linestyle=dotted,linewidth=1.5pt](5.08,0.2)(5.08,1.75)(0,1.37)
\uput[d](5.2,0.3){$x$}
\uput[l](0,1.37){$f(x)$}
\multido{\n=0+1}{4}{\uput[l](0,\n){\n}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/50.png)
- Quel volume d'eau, au m3 près, y a-t-il dans la cuve lorsque la hauteur d'eau dans la cuve est de un mètre ?
- On rappelle que
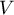 est le volume total de la cuve,
est le volume total de la cuve,  est la
fonction définie en début d'exercice et
est la
fonction définie en début d'exercice et  la fonction définie dans
la partie B.
la fonction définie dans
la partie B.
On considère l'algorithme ci-dessous.
Interpréter le résultat que cet algorithme permet d'afficher.
![\[\begin{tabular}{|ll|}\hline
Variables:&$a$ est un r\'eel\\
&$b$ est un r\'eel\\
Traitement:&$a$ prend la valeur 2\\
&$b$ prend la valeur 2 e\\
&Tant que $v(b) - v(a) > 10^{-3}$ faire :\\
&\hspace{0.4cm}\begin{tabular}{|l}
$c$ prend la valeur $(a+b)/2$\\
Si $v(c) < V/2$, alors :\\
\hspace{0.4cm}\begin{tabular}{|l}
$a$ prend la valeur c\\
\end{tabular}\\
Sinon\\
\hspace{0.4cm} \begin{tabular}{|l}
$b$ prend la valeur $c$\\
\end{tabular}\\
Fin Si\\
\end{tabular}\\
&Fin Tant que\\
Sortie: &Afficher $f(c)$\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin/55.png)
Correction exercice 3
Bac S - Amérique du nord, 1er juin 2016 6 points
Partie A
- On a
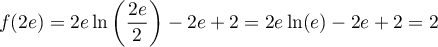 ,
car
,
car 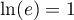 , et donc
, et donc 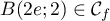 .
.
De même,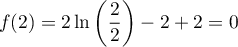 ,
car
,
car 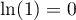 , et donc
, et donc  .
.
De plus, en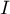 le coefficient directeur de la tangente à
le coefficient directeur de la tangente à
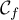 est
est  .
.
On a, pour tout ,
,
 ,
soit
,
soit 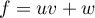 ,
avec
,
avec  , donc
, donc 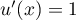 ,
,
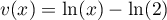 , donc
, donc 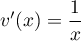 ,
et
,
et 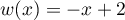 , donc
, donc 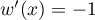 .
.
On a alors,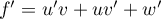 ,
soit
,
soit
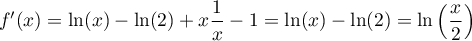 .
.
Ainsi, la tangente à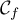 en
en 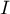 a pour coefficient
directeur
a pour coefficient
directeur 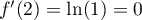 et passe par
et passe par 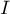 : c'est l'axe des
abscisses.
: c'est l'axe des
abscisses.
-
- Une équation de
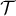 est:
est:
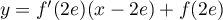 ,
avec
,
avec  et
et 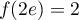 ,
d'où
,
d'où
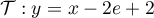 .
.
On a alors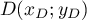 avec
avec 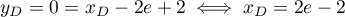 .
Ainsi,
.
Ainsi, 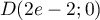 .
.
- L'aire de
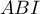 , trangle rectangle en
, trangle rectangle en 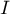 , est
, est

et l'aire du trapèze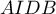 est
est
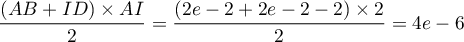 .
.
Ainsi le volume de la cuve est tel que
de la cuve est tel que
![\[5e\leqslant V\leqslant 5(4e-6)\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/39.png)
soit approximativement
![\[17,18\leqslant V\leqslant 24,37\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/40.png)
- Une équation de
-
- On a
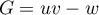 avec
avec 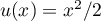 , donc
, donc 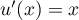 ,
,
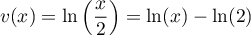 , donc
, donc 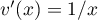 ,
et
,
et 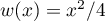 , donc
, donc 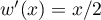 .
.
On a alors,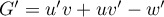 ,
soit
,
soit
![\[\begin{array}{ll}
G'(x)&=x\ln\lp\dfrac{x}2\rp+\dfrac{x^2}{2}\tm\dfrac1x-\dfrac{x}{2}\\[1em]
&=x\ln\lp\dfrac{x}{2}\rp+\dfrac{x}{2}-\dfrac{x}{2}\\[.8em]
&=g(x)\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/49.png)
ce qui montre que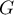 est bien une primitive de
est bien une primitive de 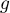 .
.
- On en déduit qu'une primitive de
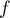 définie par
définie par
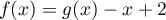 est donnée par
est donnée par
![\[F(x)=G(x)-\dfrac12x^2+2x\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/54.png)
- On peut alors calculer l'intégrale:
![\[\begin{array}{ll}
S&\dsp=\int_2^{2e}\Bigl(2-f(x)\Bigr)dx\\[1em]
&=\Bigl[ 2x-F(x)\Bigr]_2^{2e}\\[1em]
&=\Bigl[ -G(x)+\dfrac12x^2\Bigr]_2^{2e}\\[1em]
&=-G(2e)+\dfrac12(2e)^2-\Bigl(-G(2)+\dfrac122^2\Bigr)\\[.7em]
&=G(2)-G(2e)+2e^2-2
\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/55.png)
avec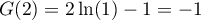 ,
et
,
et 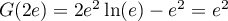 ,
donc
,
donc
![\[S=-1-e^2+2e^2-2=e^2-3\]](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/58.png)
et on en déduit le volume de la cuve: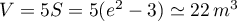 .
.
- On a
Partie B
- Le volume est
 avec
avec 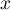 tel que
tel que 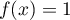 .
On cherche donc à résoudre l'équation
.
On cherche donc à résoudre l'équation  ,
avec
,
avec 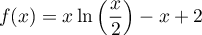 .
.
On ne sait pas résoudre excactement cette équation. On peut par contre le faire de manière approchée, en utilisant le théorème des valeurs intermédiaires.
On sait que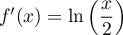 , d'après A.1.
et donc, comme
, d'après A.1.
et donc, comme 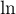 est strictement croissante sur
est strictement croissante sur 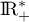 ,
que pour tout
,
que pour tout ![$x\in[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/68.png) ,
,
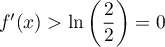 .
.
Ainsi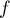 est strictement croissante sur
est strictement croissante sur ![$[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/71.png) , avec de plus
, avec de plus
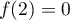 et
et 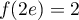 .
On en déduit, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
qu'il existe une unique solution
.
On en déduit, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
qu'il existe une unique solution ![$\alpha\in[2;2e]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/74.png) à l'équation
à l'équation
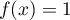 .
.
Avec la calculatrice (à l'aide d'un tableau de valeurs, ou par dichotomie par exemple), on trouve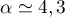 , et alors
le volume est de
, et alors
le volume est de 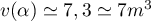 .
.
- Cet algorithme est un algorithme de recherche par dichotomie.
Il permet de chercher les valeurs d'un encadrement![$[a;b]$](/Generateur-Devoirs/TS/ChapIntegration/ex2016-Amerique-du-nord-juin_c/78.png) pour lequel
la hauteur
pour lequel
la hauteur  correspond à la moitié de la cuve.
correspond à la moitié de la cuve.
Cet encadrement permet d'avoir un résultat précis à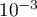 près.
près.
Cacher la correction
Quelques autres devoirs
intégration, Calculs d'intégrales - Suite d'intégrales (Bac S, 19 juin 2014) - Dimensionnement d'un récupérateur d'eau (Bac S - Amérique du nord, 1er juin 2016)
intégration, Calculs d'intégrales - Aire sous une courbe (Bac S - métropole, 11 septembre 2014) - Aire entre deux courbes (Bac S, juin 2008)
sur les intégrales: calcul d'intégrales, suite d'intégrales, et un calcul de volume
sur les intégrales: calcul d'intégrales, suite d'intégrales
Quelques exercices corrigés
Exercices corrigés
Bac 2014 (Antilles-Guyane) - Étude de fonctions, limites, TVI, tangente, intégrale
Exercices corrigés
Bac 2024 (19 juin): Logarithme, variation, limites et TVI, convexité et intégrale
Exercices corrigés
Bac 2013 - Fonction avec log, dérivée, limites, TVI, algorithme, intégrale
Exercices corrigés
Calculs d'intégrales
Exercices corrigés
Calculs d'intégrales (bis)
Voir aussi:
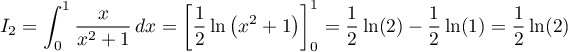
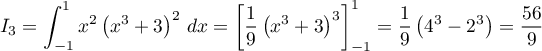
![\[\begin{array}{ll}I_4&=\dsp\int_0^1xe^{2x}\,dx\\[1em]
&=\left[ \dfrac12xe^{2x}\rb_0^1-\dsp\int_0^1\dfrac12e^{2x}\,dx\\[1em]
&=\dfrac12e^2-\lb\dfrac14e^{2x}\rb_0^1\\[1em]
&=\dfrac12e^2-\lp\dfrac14e^2-\dfrac14e^0\rp\\[1em]
&=\dfrac14e^2+\dfrac14
\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex0_c/8.png)