Bac 2024 (19 juin): Logarithme, variation, limites et TVI, convexité et intégrale
Exercice corrigé - Spécialité maths, terminale générale
Partie A : étude de la fonction 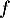
La fonction
-
- Déterminer, en justifiant, les limites de
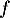 en 0 et en
en 0 et en 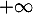 .
.
- Montrer que pour tout
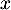 appartenant à
appartenant à ![$] 0$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/13.png) ;
; 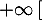 , on a :
, on a : 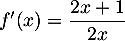 .
.
- Étudier le sens de variation de
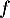 sur
sur ![$] 0 ;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/17.png) .
.
- Étudier la convexité de
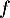 sur
sur ![$] 0 ;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/19.png) .
.
- Déterminer, en justifiant, les limites de
-
- Montrer que l'équation
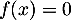 admet dans
admet dans ![$] 0 ;+\infty$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/21.png) [ une solution unique qu'on notera
[ une solution unique qu'on notera 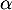 et justifier que
et justifier que 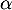 appartient à l'intervalle
appartient à l'intervalle ![$[1 ; 2]$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/24.png) .
.
- Déterminer le signe de
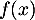 pour
pour ![$x \in] 0 ;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/26.png) .
.
- Montrer que
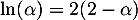 .
.
- Montrer que l'équation
Partie B : étude de la fonction 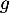
La fonction
On admet que la fonction
- Calculer
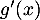 pour
pour ![$x \in] 0 ; 1]$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/36.png) puis vérifier que
puis vérifier que 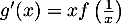 .
.
-
- Justifier que pour
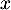 appartenant à l'intervalle
appartenant à l'intervalle ![$] 0 ; \frac1\alpha\left[\right.$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/39.png) , on a
, on a 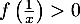 .
.
- On admet le tableau de signes suivant :
![\[ \renewcommand{\arraystretch}{1.4}
\begin{tabular}{|c|ccccc|}\hline
$x$ & 0 && $\frac1\alpha$ && 1 \\
\hline
Signe de $f\lp\frac{1}{x}\rp$ && $+$ & 0 & $-$& \\\hline
\end{tabular}
\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/41.png)
- Justifier que pour
Partie C : un calcul d'aire
On a représenté sur le graphique ci-dessous :
- La courbe
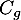 de la fonction
de la fonction 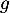 ;
;
- La parabole
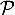 d'équation
d'équation 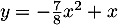 sur l'intervalle
sur l'intervalle ![$\left.] 0 ; 1\right]$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/46.png) .
.
![\[\psset{unit=10cm,arrowsize=7pt}
\begin{pspicture*}(-.4,-.2)(1.2,.5)
\newcommand{\fctg}[1]{-7 8 div #1 2 exp mul #1 add
-0.25 #1 2 exp mul #1 ln mul
add}
\newcommand{\fctP}[1]{-7 8 div #1 2 exp mul #1 add}
\pscustom{
\psplot{.58}{1}{\fctg{x}} \gsave
\psplot{1}{.58}{\fctP{x}}
\fill[fillstyle=hlines,fillcolor=lightgray]
%\fill[fillstyle=vlines]
\grestore}
\psline{->}(-.05,0)(1.2,0)
\psline{->}(0,-.05)(0,.5)
\newcommand{\divdx}[1]{#1 10 div}
\multido{\i=0+1}{11}{\psline(! \divdx{\i} \space .01)(! \divdx{\i} \space -.01)
\psline[linestyle=dotted](! \divdx{\i} \space -.01)(! \divdx{\i} \space .5)}
\multido{\i=1+1}{4}{\psline(! .01 \space \divdx{\i})(! -.01 \space \divdx{\i})
\psline[linestyle=dotted](! .01 \space \divdx{\i})(! 1.1 \space \divdx{\i})}
\psplot{.001}{1}{\fctg{x}}
\psplot{.001}{1}{\fctP{x}}
\psline[linestyle=dashed](.58,0)(.58,.33)
\rput(-.02,-.02){$O$}
\rput[r](-.02,.1){$0,1$}
\rput(.1,-.04){$0,1$}
\rput(.58,-.04){$\frac1\alpha$}
\psline[linestyle=dashed](1,0)(1,.12)
\rput(1,-.04){$1$}
\rput[l](.72,.33){$\mathcal{C}_g$}
\rput[l](.72,.23){$\mathcal{P}$}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/47.png)
On souhaite calculer l'aire
On rappelle que
-
- Justifier la position relative des courbes
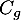 et
et 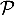 sur l'intervalle
sur l'intervalle ![$] 0 ; 1]$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/56.png) .
.
- Démontrer l'égalité :
![\[\int_{\frac1\alpha}^1 x^2 \ln x dx = \frac{-\alpha^{3}-6 \alpha+13}{9 \alpha^{3}}\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/57.png)
- Justifier la position relative des courbes
- En déduire l'expression en fonction de
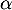 de l'aire
de l'aire 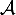 .
.
Correction
Tags:LogarithmeConvexitéIntégrales
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
