Droites du plan - Vecteur normal et équation cartésienne
Avant propos: À voir, connaître aussi, avant:
La notion fondamentale pour tout ce qui suit: l'orthogonalité de deux vecteurs. Exercices corrigés sur le produit scalaire:
Vecteur normal - Définition et propriétés
Définition
Un vecteur ![\[\begin{pspicture}(-1,-1)(4.5,1.8)
\psline(-0.9,-0.3)(4.2,1.4)\rput(3.7,1.5){$d$}\psline[linewidth=1.5pt,linecolor=red]{->}(.6,.2)(.25,1.5)\rput(-.1,.8){\red$\V{n}$}\psline(.5,.5)(.85,.63)(.95,.3)\end{pspicture}\]](Cours-normal-IMG/4.png)
Conséquences:
- Si
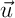 est un vecteur directeur de
est un vecteur directeur de  , on a
, on a
 .
.
(voir, pour le produit scalaire et avec des coordonnées)
- Si
 est un point de la droite
est un point de la droite  , alors
, alors  est
l'ensemble des points
est
l'ensemble des points 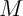 du plan tels que
du plan tels que 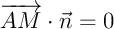 .
.
Propriété
Le vecteur Exercices corrigés
Exercice 1
Soit Donner un vecteur normal et un vecteur directeur de
Exercice 2
Déterminer l'équation de la droite de vecteur normal Exercice 3
Soit Déterminer l'équation de la droite
Exercice 4
- Déterminer une équation de la médiatrice du segment
![$[AB]$](Cours-normal-IMG/57.png) .
.
- Déterminer une équation de la hauteur issue de
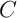 dans le
triangle
dans le
triangle 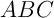 .
.
Exercice 5
Dans un RON, on considère les points
- Déterminer une équation de la droite
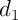 perpendiculaire à
perpendiculaire à
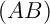 et passant par
et passant par 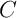 .
.
- Déterminer une équation de la droite
 parallèle à
parallèle à
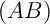 et passant par
et passant par  .
.
Voir aussi