Détermination de l'expression d'une fonction du 2nd degré
Exercice corrigé - maths en seconde générale
Énoncé
|
On considère la fonction où On souhaite que la courbe représentative |
![$$(-2,1.)(2,8)
\psline[linewidth=1pt]{->}(-2.3,0)(3.5,0)
\psline[linewidth=1pt]{->}(0,-0.4)(0,8.5)
\rput(-0.3,-0.3){$O$}
\rput(1,-0.3){$1$}\rput(-0.15,1.25){$1$}
\multido{\i=-2+1}{6}{\psline[linewidth=0.4pt,linestyle=dashed](\i,-0.15)(\i,8.2)}
\multido{\i=1+1}{8}{\psline[linewidth=0.4pt,linestyle=dashed](-2.2,\i)(3.2,\i)}
\psplot[linewidth=1.3pt]{-1.5}{3.1}{x 2 exp -2 x mul add 3 add}
\rput(-1.65,7.5){$\mathcal{C}_f$}
\rput(-1,6){\Large $\tm$}\rput(-1.3,5.7){$A$}
\rput(1,2){\Large $\tm$}\rput(1.3,1.7){$B$}
$$](/Generateur-Devoirs/2nde/Chap4/ex3/12.png) |
Correction
 appartient à
appartient à 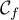 ,
donc,
,
donc, 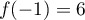 , soit
, soit
![\[\begin{array}{ll}f(-1)&=(-1)^2+a(-1)+b\\[.4em]&=1-a+b=6\enar\]](/Generateur-Devoirs/2nde/Chap4/ex3_c/4.png)
De même le point appartient à
appartient à 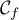 ,
donc,
,
donc, 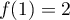 , soit
, soit
![\[\begin{array}{ll}f(1)&=1^2+a\tm1+b\\[.4em]&=1+a+b=2\enar\]](/Generateur-Devoirs/2nde/Chap4/ex3_c/8.png)
En résumé, on a le système de deux équations:
![\[\la\begin{array}{rcrcrcc}
1 &-& a &+& b &=& 6 \\ 1 &+& a &+& b &=& 2\end{array}
\right.
\iff
\la\begin{array}{rcrcc}
-a &+& b &=& 5 \\ a &+& b &=& 1\end{array}
\right.\]](/Generateur-Devoirs/2nde/Chap4/ex3_c/9.png)
En ajoutant les deux équations, on trouve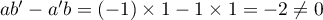 , soit
, soit  .
.
En soustrayant les deux équations, on trouve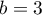 soit
soit  .
.
En remplaçant finalement les valeurs trouvées pour et
et 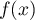 dans l'expression
de
dans l'expression
de 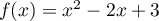 , on trouve donc l'expression:
, on trouve donc l'expression:
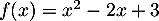 .
.
Correction
Le pointDe même le point
En résumé, on a le système de deux équations:
En ajoutant les deux équations, on trouve
En soustrayant les deux équations, on trouve
En remplaçant finalement les valeurs trouvées pour
Tags:SystèmesFonctions
Voir aussi:
Quelques devoirs
sur quelques équations à résoudre, systèmes d'équations à deux inconnues, et la construction géométrique graphique de points et vecteurs
sur les vecteurs et coordonnées: calculs de coordonnées, et montrer l'alignement de points. Quelques équations et un système à résoudre
résolution de systèmes d'équations, les vecteurs (vecteurs colinéaires et alignement de points), et la courbe d'une fonction
sur les systèmes d'équations, les vecteurs (vecteurs colinéaires et alignement de points), et étude du sens de variation d'une fonction
tableau de signe - Intersection et position relative de deux courbes - Taux d'évolution successifs - Système d'équations - Équations cartésienne de droites et intersection de droites - Probabilité: un jeu avec un dé - Probabilité: patisserie à la crème ou aux fruits
