Généralités sur les fonctions

Courbe représentative, lecture graphique & variation

Généralités - Définitions

Définition

Une fonction est un objet mathématique qui permet d'associer à un nombre, un unique autre nombre.
Le nombre associé s'appelle l'image du nombre de départ qui s'appelle de son côté l'antécédent.

Une telle fonction f étant donnée, on peut calculer, pour diverses antécédents, les images correspondantes.
Pour essayer de "comprendre" cette fonction, cette liste de valeurs images n'est pas forcément très parlante, et on peut les placer sur un graphique afin d'essayer d'observer le comportement de la fonction.
Par exemple:

y = f (x)

Avec "beaucoup" d'observations, on peut commencer à deviner l'allure de la courbe, le comportement de la fonction (si elle augmente, diminue, si elle a un maximum ou non, … )
L'étude de fonctions en mathématiques vise justement à trouver ces propriétés à partir, en général, de l'expression algébrique de la fonction.

Courbe représentative d'une fonction

Définition:

La courbe représentative C_f de la fonction f est l'ensemble des points M(x ; y) tels que y = f (x).
En d'autres termes, un point M(x ; y) appartient à la courbe représentative C_f de la fonction f si et seulement si :

M(x ; y) ∈ C_f ⇔ y = f (x)

Lecture graphique d'images et d'antécédents

Exercice 1

Le graphique ci-dessous donne la courbe représentative C_f d'une fonction f.
Les points A(−3 ; 3), B(−2 ; −1), C(−1 ; −2), D(0 ; −1), E(1 ; 0,9), F(3 ; 2) et G(4 ; −1) appartiennent à la courbe C_f.

L'image de 3 par f est f (3) =
Le point sur la courbe d'abscisse 3 est le point F, dont l'ordonnée est donc justement l'image de 3.
L'image de −2 par f est f (−2) =
Le point sur la courbe d'abscisse −2 est le point B, dont l'ordonnée est donc justement l'image de −2.
D'après le point E, un antécédent de 0,9 par f est f ( ) = 0,9
Le point sur la courbe d'ordonnée 0,9 est le point E, dont l'abscisse est donc justement l'antécédent de 0,9.
Le nombre d'antécédents de −1 par f est
Il y a 3 antécédents de −1 par f: x = −2 (point B), x = 0 (point D) et x = 4 (point G).
Le nombre de solutions de l'équation f (x) = 2 est
On compte le nombre de points de la courbe qui ont comme ordonnée 2.
Les abscisses de ces points sont alors les solutions de cette équation: il y en a ici 3: x≃−2,9, x≃1,9 et x = 3 (point F).
Le nombre de solutions de l'équation f (x) = 3 est
On compte le nombre de points de la courbe qui ont comme ordonnée 3.
Les abscisses de ces points sont alors les solutions de cette équation: il y en a ici une seule, x = 3 (point A).
Dresser le tableau de variation de la fonction f.

x −∞ −1 ≃2,4 +∞

≃2,2

f ↘ ↗ ↘

−2

Calculs de coordonnées de points sur une courbe

Exercice 2:

Soit f la fonction définie par l'expression: f (x) = 2x² + 3, et C_f sa courbe représentative.
Cocher, parmi les points suivants, ceux qui appartiennent à la courbe C_f.
A(0;3) − B(1;6) − C(2;11) − D(−2;−11) − E(−2;11) − F(5;53)

Exercice 3:

Soit f la fonction définie par l'expression: f (x) = −x² + 2x − 3.

Compléter le tableau de valeurs de la fonction f suivant:

x −4 −2 0 2 4

y = f (x)
Tracer l'allure la courbe représentative C_f de f.

Sens de variation d'une fonction

Propriété

On dit qu'une fonction f est croissante sur un intervalle I lorsqu'elle conserve l'ordre sur cet intervalle: pour tout couple (a ; b) de I,
a ≤ b ⇔ f (a) ≤ f (b)
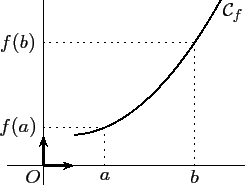
On dit qu'une fonction f est décroissante sur un intervalle I lorsqu'elle change (ou inverse) l'ordre sur cet intervalle: pour tout couple (a ; b) de I,
a ≤ b ⇔ f (a) ≥ f (b)

x	−∞		−1		≃2,4		+∞
					≃2,2
f		↘		↗		↘
			−2

x	−4	−2	0	2	4
y = f (x)

x	−∞		−5		3		7		22		+∞
					1				−2
f		↘		↗		↘		↗		↘
			0,5				−8