Devoir de maths corrigé, Probabilité et inéquations (tableaux de signes)
seconde
Devoir de mathématiques, et corrigé, sur les probabilités (arbres de probabilités), et quelques inéquations (tableaux de signes), posé en seconde générale, année scolaire 2023/2024
Exercice 1: Des trinômes d'élèves qui connaissent leur cours
Dans une classe de 30 élèves, 10 élèves connaissent parfaitement leur
cours.
Je désigne dans cette classe successivement trois élèves au hasard pour former un groupe de travail.
1. On note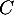 :"l'élève désigné connaît parfaitement son cours"
:"l'élève désigné connaît parfaitement son cours"
Cacher la correction
Je désigne dans cette classe successivement trois élèves au hasard pour former un groupe de travail.
- Dresser un arbre de probabilités décrivant la situation.
- Quelle est la probabilité pour que, dans ce groupe, aucun élève ne connaisse parfaitement son cours ?
- Quelle est la probabilité pour que tous les élèves du groupe connaissent parfaitement leur cours ?
- Quelle est la probabilité pour qu'au moins un élève du groupe connaisse parfaitement son cours ?
Correction exercice 1
1. On note
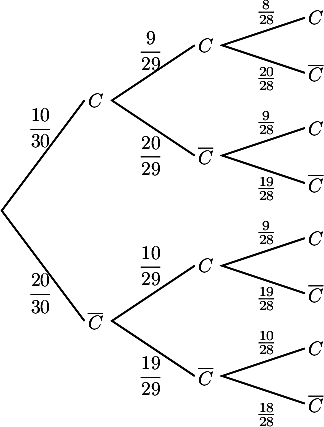 |
|
2. Ainsi, d'après la question 2., la probabilité est d'environ |
Cacher la correction
Exercice 2: Chaîne de production de vêtements avec des défauts
Une chaîne de production d'une usine fabrique des vêtements.
Une étude statistique a montré que:
On note par la suite les événements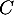 : "le vêtement présente un défaut de couleur"
et
: "le vêtement présente un défaut de couleur"
et  : "le vêtement présente un défaut dans la forme".
: "le vêtement présente un défaut dans la forme".
Cacher la correction
- 12% des vêtements ont un défaut de couleur,
- parmi les vêtements ayant un défaut de couleur, 20% ont un défaut dans la forme,
- parmi les vêtements n'ayant pas de défaut de couleur, 8% présentent un défaut dans la forme.
On note par la suite les événements
- Compléter l'arbre pondéré suivant décrivant la situation:
![\[\psset{xunit=1cm,yunit=.4cm}
\begin{pspicture}(-2,-3)(5,2.6)
\psline(0,0)(1.5,1.5)\rput(1.75,1.5){$C$}
\psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$F$}
\psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{F}$}
%
\psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{C}$}
\psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$F$}
\psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{F}$}
\end{pspicture}\]](/Generateur-Devoirs/2nde/Chap9/exdefauts/3.png)
-
- Calculer la probabilité que le vêtement prélevé ait un défaut de couleur et un défaut dans la forme.
- Calculer la probabilité que le vêtement prélevé ait un défaut de forme.
- Le directeur de l'usine affirme que 92% des vêtements fabriqués ne présentent aucun défaut. Cette affirmation est-elle correcte ? Expliquer.
- Les employés de l'usine peuvent acheter des vêtements
à tarif préférentiel.
L'un d'entre eux achète 8 vêtements.
Quelle est la probabilité pour qu'aucun des vêtements achetés ne présente de défaut ?
Correction exercice 2
-
![\[\psset{xunit=1.cm,yunit=.5cm}
\begin{pspicture}(-2,-1.5)(5,1)
\psline(0,0)(1.5,1.5)\rput(1.75,1.5){$C$}\rput(0.7,1.2){$12\%$}
\psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$F$}\rput(2.9,2.2){$20\%$}
\psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{F}$}\rput(2.9,0.7){$80\%$}
%
\psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{C}$}\rput(0.7,-1.2){$88\%$}
\psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$F$}\rput(2.9,-0.7){$8\%$}
\psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{F}$}\rput(2.9,-2.2){$92\%$}
\end{pspicture}\]](/Generateur-Devoirs/2nde/Chap9/exdefauts_c/1.png)
-
-
- La probabilité qu'un vêtement ne présente aucun défaut
est
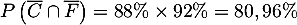 .
.
Le directeur de l'usine se trompe donc. - On note l'événement A: "le vêtement n'a pas de défaut" qui a la probabilité
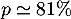 .
.
On a alors l'arbre, en prenant successivement 8 vêtements:
![\[\psset{xunit=1.cm,yunit=.5cm}
\begin{pspicture}(0,-3)(9,3.5)
\psline(0,0)(1.5,1.5)\rput(1.75,1.5){$A$}\rput(0.7,1.2){$81\%$}
\psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$A$}\rput(2.9,2.2){$81\%$}
\psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{A}$}\rput(2.9,0.7){$19\%$}
%
\psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{A}$}\rput(0.7,-1.2){$19\%$}
\psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$A$}\rput(2.9,-0.7){$81\%$}
\psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{A}$}\rput(2.9,-2.2){$19\%$}
%
\rput(5,0){$\dots$}\rput(5,-2){$\dots$}
%
\psline(5.5,2)(4,2.25)(5.5,2.5)\rput(5.75,2.5){$A$}\rput(5,2.75){\small$81\%$}\rput(5.9,1.8){$\dots$}
\psline(6,2.5)(6.8,2.75)\rput(7.2,2.75){$\dots$}
\psline(7.6,2.75)(8.5,3)\rput(8.8,3.2){$A$}\rput(8,3.25){\small$81\%$}
\end{pspicture}\]](/Generateur-Devoirs/2nde/Chap9/exdefauts_c/6.png)
Il n'y a qu'un seul chemin correspondant à l'événement "aucun des 8 vêtements n'a un défaut" dont la probabilité est donc de
![\[p\simeq(81\%)^8\simeq0,185=18,5\%\]](/Generateur-Devoirs/2nde/Chap9/exdefauts_c/7.png)
Cacher la correction
Exercice 3: Pile ou face avec une pièce sur deux truquée
J'ai dans ma poche deux pièces de monnaie, indiscernables au toucher.
Une des deux pièces est bien équilibrée, l'autre est truquée:
lorsqu'on la lance, on obtient "Pile" neuf fois sur dix.
Je prend une pièce au hasard dans ma poche et la lance. Quelle est la probabilité d'obtenir "Pile" ?
Je prend une pièce au hasard dans ma poche et la lance. Quelle est la probabilité d'obtenir "Pile" ?
Exercice 4: Deux inéquations à résoudre
Résoudre les inéquations :
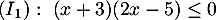
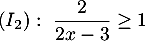
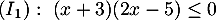
On peut directement dresser le tableau de signe du produit:
![\[\begin{tabular}[t]{|c|ccccccc|}\hline
$x$&$-\infty$ & & $-3$ & & $\frac{5}{2}$ & & $+\infty$ \\\hline
$x+3$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ &\\\hline
$2x-5$ & & $-$ & $|$ & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ &\\\hline
$(x-3)(5-x)$ & & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap3/ex1_c/2.png)
D'après le tableau de signes, les solutions de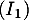 sont
sont
![$\mathcal{S}=\left[-3;\dfrac{5}{2}\right]$](/Generateur-Devoirs/2nde/Chap3/ex1_c/4.png)
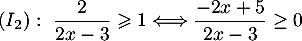
![\[\begin{tabular}[t]{|c|ccccccc|}\hline
$x$&$-\infty$ & & $\frac{3}{2}$ & & $\frac{5}{2}$ & & $+\infty$ \\\hline
$-2x+5$ & & $+$ & $|$ & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
$2x-3$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ &\\\hline
$\frac{-2x+5}{2x-3}$ & & $-$ & \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap3/ex1_c/6.png)
D'après le tableau de signes, les solutions de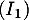 sont
sont
![$\mathcal{S}=\Big]\dfrac{3}{2};\dfrac{5}{2}\Big]$](/Generateur-Devoirs/2nde/Chap3/ex1_c/8.png)
Cacher la correction
Correction exercice 4
On peut directement dresser le tableau de signe du produit:
![\[\begin{tabular}[t]{|c|ccccccc|}\hline
$x$&$-\infty$ & & $-3$ & & $\frac{5}{2}$ & & $+\infty$ \\\hline
$x+3$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ &\\\hline
$2x-5$ & & $-$ & $|$ & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ &\\\hline
$(x-3)(5-x)$ & & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap3/ex1_c/2.png)
D'après le tableau de signes, les solutions de
![\[\begin{tabular}[t]{|c|ccccccc|}\hline
$x$&$-\infty$ & & $\frac{3}{2}$ & & $\frac{5}{2}$ & & $+\infty$ \\\hline
$-2x+5$ & & $+$ & $|$ & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
$2x-3$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ &\\\hline
$\frac{-2x+5}{2x-3}$ & & $-$ & \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap3/ex1_c/6.png)
D'après le tableau de signes, les solutions de
Cacher la correction
Exercice 5: Intersection et position relative de deux courbes
On considère les fonctions 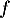 et
et 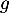 définies par
les expressions
définies par
les expressions 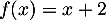 et
et 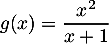 ,
et on note
,
et on note 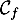 et
et 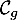 leurs courbes représentatives.
leurs courbes représentatives.
Cacher la correction
- Préciser l'ensemble de définition de
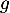 .
.
- Déterminer les coordonnées des éventuels points d'intersection des courbes
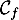 et
et 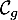 .
.
- On dit que la courbe
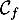 est au-dessus de la courbe
est au-dessus de la courbe 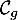 lorsque
lorsque 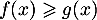 .
.
Déterminer l'ensemble des valeurs de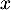 pour lesquelles la courbe
pour lesquelles la courbe 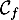 est au-dessus de la courbe
est au-dessus de la courbe 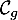 .
.
Correction exercice 5
- La fonction
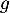 est définie lorsque
est définie lorsque 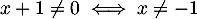 ,
et l'ensemble de définition de
,
et l'ensemble de définition de 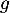 est donc
est donc
![\[\mathcal{D}_g=\R\setminus\la-1\ra\]](/Generateur-Devoirs/2nde/Chap3/ex8_c/4.png)
- Si
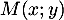 est un éventuel point d'intersection, alors on a
est un éventuel point d'intersection, alors on a
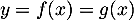 .
.
En particulier,
![\[\begin{array}{ll}f(x)=g(x)\iff x+2=\dfrac{x^2}{x+1}
\iff x+2-\dfrac{x^2}{x+1}=0\\
\iff\dfrac{(x+2)(x+1)}{x+1}-\dfrac{x^2}{x+1}=0\\
\iff\dfrac{3x+2}{x+1}=0\\
\iff \left( x\not=-1 \text{ et } x=-\dfrac23\rp\enar\]](/Generateur-Devoirs/2nde/Chap3/ex8_c/7.png)
L'ordonnée du point d'intersection est alors
![\[y=f\lp-\dfrac23\rp=-\dfrac23+2=\dfrac43\]](/Generateur-Devoirs/2nde/Chap3/ex8_c/8.png)
Le point d'intersection est donc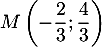 .
.
- On cherche à résoudre l'inéquation
![\[f(x)\geqslant g(x)
\iff f(x)-g(x)\geqslant 0
\iff x+2-\dfrac{x^2}{x+1}
=\dfrac{3x+2}{x+1}\geqslant0\]](/Generateur-Devoirs/2nde/Chap3/ex8_c/10.png)
que l'on résout grâce à un tableau de signes:
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-1$ && $-\frac23$ && $+\infty$ \\\hline
$3x+2$ && $-$ & $|$ & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \\\hline
$x+1$ && $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ & \\\hline
$\dfrac{3x+2}{x+1}$ && $+$ &\db& $-$ &\zb& $+$ & \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap3/ex8_c/11.png)
On trouve finalement que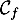 est au-dessus de
est au-dessus de 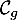 pour
pour ![$x\in]-\infty;-1[\cup[-\frac23;+\infty[$](/Generateur-Devoirs/2nde/Chap3/ex8_c/14.png)
Cacher la correction
Quelques autres devoirs
sur les équations, inéquations et tableaux de signes
sur les inéquations et tableaux de signes, et statistiques: moyenne, écart type, médianne et quartile, et représentation graphique par un diagramme en boîtes (ou boîtes à moustaches)
Statistiques: calculs de la moyenne et de l'écart type d'une série pondérée. Résolution d'inéquations. Ensemble de de définition de fonctions. Exercice complet sur les fonctions: sens de variation, courbe représentative et résolution graphique d'inéquations.
pourcentage et évolutions (taux global), résolution d'inéquations (tableaux de signes), et un problème complet avec des fonctions (bénéfice d'une société, rentabilité et bénéfice maximal)
pourcentage et probabilités, et deux tableaux de signes. Intersection de deux courbes
Quelques exercices corrigés
Exercices corrigés
Factorisations
Exercices corrigés
3 équations du 1er degré
Exercices corrigés
Factorisation, développement et résolution d'équations
Exercices corrigés
Vérification de la solution d'une équation - Calcul sur les radicaux et fractions
Exercices corrigés
Vérification de la solution d'une équation - Calcul sur les radicaux et fractions
Voir aussi:
{Pi\`ece truqu\'ee}\rput(0.7,1.2){$\dfrac12$}
\psline(4,1.5)(5.5,2.25)\rput(5.75,2.25){$P$}\rput(4.7,2.2){$\dfrac{9}{10}$}
\psline(4,1.5)(5.5,0.75)\rput(5.75,0.75){$F$}\rput(4.7,0.7){$\dfrac{1}{10}$}
%
\psline(0,0)(1.5,-1.5)
\rput[l](1.6,-1.5){Pi\`ece non truqu\'ee}\rput(0.7,-1.2){$\dfrac12$}
\psline(4,-1.5)(5.5,-0.75)\rput(5.75,-0.75){$P$}\rput(4.7,-0.7){$\dfrac12$}
\psline(4,-1.5)(5.5,-2.25)\rput(5.75,-2.25){$F$}\rput(4.7,-2.2){$\dfrac12$}
\end{pspicture}\]](/Generateur-Devoirs/2nde/Chap9/ex4.0_c/1.png)