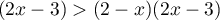Devoir de maths corrigé, Statistiques, inéquations (graphique)
seconde
Devoir de mathématiques, et corrigé, sur statistiques, les fonctions (graphique, courbe et inéquation) et la résolution d'inéquations (tableaux de signes), posé en seconde générale, année scolaire 2023/2024
Exercice 1: Moyenne et écart type d'une série pondérée - Sujet A
Donner la moyenne et l'écart-type de la série:
![\[\begin{tabular}{|*{6}{c|}}\hline
Valeurs & 12 & 5 & 8 & 9 \\\hline
Effectifs & 3 & 2 & 1 & 4 \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap8/ex0/1.png)
(Détailler les formules et calculs effectués.)
La moyenne de la série est:
![\[\overline{x}=\dfrac{3\tm12+2\tm5+1\tm8+4\tm9}{10}
=9\]](/Generateur-Devoirs/2nde/Chap8/ex0_c/1.png)
La variance de la série est:
![\[
V=\dfrac{3\tm(12-9)^2+2\tm(5-9)^2+1\tm(8-9)^2+4\tm(9-9)^2}{10}
=6
\]](/Generateur-Devoirs/2nde/Chap8/ex0_c/2.png)
d'où l'écart-type: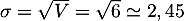
Cacher la correction
(Détailler les formules et calculs effectués.)
Correction exercice 1
La moyenne de la série est:
La variance de la série est:
d'où l'écart-type:
Cacher la correction
Exercice 2: Moyenne et écart type d'une série pondérée - Sujet B
Donner la moyenne et l'écart-type de la série:
![\[\begin{tabular}{|*{6}{c|}}\hline
Valeurs & 14 & 5 & 18 & 10 \\\hline
Effectifs & 3 & 2 & 1 & 4 \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap8/ex0B/1.png)
(Détailler les formules et calculs effectués.)
La moyenne de la série est:
![\[\overline{x}=\dfrac{3\tm14+2\tm5+1\tm18+4\tm10}{10}
=11\]](/Generateur-Devoirs/2nde/Chap8/ex0B_c/1.png)
La variance de la série est:
![\[
V=\dfrac{3\tm(14-11)^2+2\tm(5-11)^2+1\tm(18-11)^2+4\tm(10-11)^2}{10}
=15,2
\]](/Generateur-Devoirs/2nde/Chap8/ex0B_c/2.png)
d'où l'écart-type: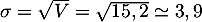
Cacher la correction
(Détailler les formules et calculs effectués.)
Correction exercice 2
La moyenne de la série est:
La variance de la série est:
d'où l'écart-type:
Cacher la correction
Exercice 3: Résolution d'inéquations
Résoudre les inéquations:
Cacher la correction
Correction exercice 3
- On dresse le tableau de signe de l'expression:
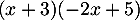
![\[
\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-3$ && $\frac{5}{2}$ && $+\infty$ \\\hline
$x+3$ && $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ & \\\hline
$-2x+5$ && $+$ & $|$ & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
$(x+3)(-2x+5)$ && $-$ &\zb& $+$ &\zb& $-$ & \\\hline
\end{tabular}
\]](/Generateur-Devoirs/2nde/Chap3/ex4_c/2.png)
Ainsi,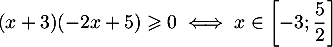 .
.
-
![$\begin{array}[t]{ll}
(2x-3) > (2-x)(2x-3)
&\iff
(2x-3)-(2-x)(2x-3)> 0 \\
&\iff
(2x-3)\Bigl[ 1 - (2-x)\Bigr] > 0 \\
&\iff
(2x-3)(x-1)> 0
\enar$](/Generateur-Devoirs/2nde/Chap3/ex4_c/4.png)
![\[
\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $1$ && $\frac{3}{2}$ && $+\infty$ \\\hline
$2x-3$ && $-$ & $|$ & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \\\hline
$x-1$ && $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ & \\\hline
$(2x-3)(x-1)$ && $+$ &\zb& $-$ &\zb& $+$ & \\\hline
\end{tabular}
\]](/Generateur-Devoirs/2nde/Chap3/ex4_c/5.png)
Ainsi,![$(2x-3) > (2-x)(2x-3) \iff x\in]-\infty;1[\cup]\frac{3}{2};+\infty[$](/Generateur-Devoirs/2nde/Chap3/ex4_c/6.png) .
.
-
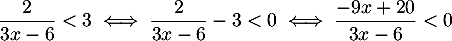
![\[
\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $2$ && $\frac{20}{9}$ && $+\infty$ \\\hline
$-9x+20$ && $+$ & $|$ & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
$3x-6$ && $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ & \\\hline
$\dfrac{-9x+20}{3x-6}$ && $-$ &\db& $+$ &\zb& $-$ & \\\hline
\end{tabular}
\]](/Generateur-Devoirs/2nde/Chap3/ex4_c/8.png)
Ainsi,![$\dfrac{2}{3x-6}< 3
\iff x\in \Bigl]-\infty;2\Bigr[\cup\Bigl[\frac{20}{9};+\infty\Bigr[$](/Generateur-Devoirs/2nde/Chap3/ex4_c/9.png)
Cacher la correction
Exercice 4: Ensemble de définition de deux fonctions
Déterminer l'ensemble de définition des fonctions  ,
,  et
et  dont les expressions sont:
dont les expressions sont:

 .
On ne doit pas avoir
.
On ne doit pas avoir
 .
Ainsi,
.
Ainsi,  .
.
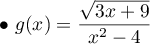 On ne doit pas avoir
On ne doit pas avoir  et
et  ,
soit
,
soit  et
et  ou
ou  .
.
Ainsi, .
.
 .
On doit avoir
.
On doit avoir  .
.
Pour résoudre cette inéquation, on peut dresser le tableau de signes de :
:

 .
.
Cacher la correction
Correction exercice 4
 .
Ainsi,
.
Ainsi,  .
.
Ainsi,
Pour résoudre cette inéquation, on peut dresser le tableau de signes de

Cacher la correction
Exercice 5: Fonction: variation, courbe et inéquations graphiques et algébriques
On considère la fonction  définie par l'expression
définie par l'expression 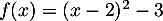 définie sur
définie sur ![$[-1;5]$](/Generateur-Devoirs/2nde/Chap5/excplt/3.png) .
.
On considère la fonction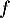 définie par l'expression
définie par l'expression 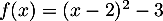 définie sur
définie sur ![$[-1;5]$](/Generateur-Devoirs/2nde/Chap5/excplt_c/3.png) .
.
Cacher la correction
- Décomposer la fonction
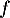 en une suite d'opérations élémentaires.
en une suite d'opérations élémentaires.
- Déterminer le sens de variation de
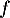 sur l'intervalle
sur l'intervalle ![$[-1;2]$](/Generateur-Devoirs/2nde/Chap5/excplt/6.png) .
.
On admet ensuite que la fonction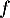 est croissante sur
est croissante sur ![$[2;5]$](/Generateur-Devoirs/2nde/Chap5/excplt/8.png) .
Donner alors le tableau de variation de
.
Donner alors le tableau de variation de 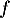 sur
sur ![$[-1;5]$](/Generateur-Devoirs/2nde/Chap5/excplt/10.png) .
.
- Tracer dans un repère l'allure de la courbe représentative de
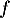 (on pourra s'aider d'un rapide tableau de valeurs).
(on pourra s'aider d'un rapide tableau de valeurs).
- Résoudre graphiquement l'inéquation
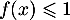 .
.
- Tracer sur le graphique précédent la courbe de la fonction
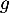 définie par
définie par 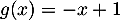 .
.
Résoudre alors graphiquement l'inéquation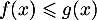 .
.
Bonus: Résoudre exactement, par le calcul, l'inéquation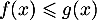 . (on pourra penser à développer l'expression de
. (on pourra penser à développer l'expression de 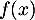 ).
).
Correction exercice 5
On considère la fonction
-
{$x-2$}
\psline{->}(2.4,0)(3.6,0)\rput(3,.3){carr\'e}
\rput[l](3.8,0){$(x-2)^2$}
\psline{->}(5.4,0)(6.6,0)\rput(5.9,.3){$-3$}
\rput[l](6.8,0){$(x-2)^2-3$}
\psline[arrowsize=7pt]{->}(0,-.3)(0,-1)(8.5,-1)(8.5,-.3)
\rput(3.5,-.7){$f$}
\end{pspicture}\]](/Generateur-Devoirs/2nde/Chap5/excplt_c/4.png)
- Soit deux nombres réels quelconques
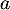 et
et 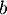 tels que
tels que
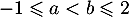
alors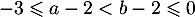
donc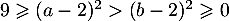 : carré de nombres négatifs change l'ordre
: carré de nombres négatifs change l'ordre
d'où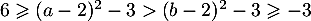
soit donc
c'est-à-dire que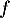 change l'ordre et est donc décroissante sur
change l'ordre et est donc décroissante sur ![$[-1;2]$](/Generateur-Devoirs/2nde/Chap5/excplt_c/13.png) .
.
On a donc trouvé le tableau de variation
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $-1$ && 2 && 5 \\\hline
&6&&&&6\\
$f$&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&$-3$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap5/excplt_c/14.png)
- Avec éventuellement un tableau de valeurs pour compléter le tableau de variation précédent:
![\[\begin{tabular}{|c|*7{p{2em}|}}\hline
$x$&$-1$&0&1&2&3&4&5\\\hline
$f(x)$&6&1&$-2$&$-3$&$-2$&1&6\\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap5/excplt_c/15.png)
(\i,7.2)\rput(\i,-.3){$\i$}}
\multido{\i=-4+1}{12}{\psline[linestyle=dashed](-1.2,\i)(5.2,\i)\rput[r](-.1,\i){$\i$}}
\psplot[linewidth=1.6pt,linecolor=red]{-1}{5}{x 2 sub 2 exp 5 sub}
\rput(4,4){\red$\mathcal{C}_f$}
\psplot[linewidth=1.6pt,linecolor=blue]{-3}{5}{-1 x mul 1 add}
\rput(-1.5,2){\blue$\mathcal{C}_g$}
\psline[linewidth=1.6pt,linecolor=magenta](-2,1)(7,1)
\end{pspicture*}\]](/Generateur-Devoirs/2nde/Chap5/excplt_c/16.png)
- Graphiquement on trouve que
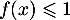 pour
pour ![$x\in[0;4]$](/Generateur-Devoirs/2nde/Chap5/excplt_c/18.png) .
.
- Graphiquement on trouve que
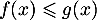 pour
pour ![$x\in[0;3]$](/Generateur-Devoirs/2nde/Chap5/excplt_c/20.png)
Cacher la correction
Quelques autres devoirs
sur les équations, inéquations et tableaux de signes
sur les inéquations et tableaux de signes, et statistiques: moyenne, écart type, médianne et quartile, et représentation graphique par un diagramme en boîtes (ou boîtes à moustaches)
Statistiques: calculs de la moyenne et de l'écart type d'une série pondérée. Résolution d'inéquations. Ensemble de de définition de fonctions. Exercice complet sur les fonctions: sens de variation, courbe représentative et résolution graphique d'inéquations.
pourcentage et évolutions (taux global), résolution d'inéquations (tableaux de signes), et un problème complet avec des fonctions (bénéfice d'une société, rentabilité et bénéfice maximal)
pourcentage et probabilités, et deux tableaux de signes. Intersection de deux courbes
Quelques exercices corrigés
Exercices corrigés
Factorisations
Exercices corrigés
3 équations du 1er degré
Exercices corrigés
Factorisation, développement et résolution d'équations
Exercices corrigés
Vérification de la solution d'une équation - Calcul sur les radicaux et fractions
Exercices corrigés
Vérification de la solution d'une équation - Calcul sur les radicaux et fractions
Voir aussi: