Devoir de maths corrigé, Probabilités et inéquations (signes)
seconde
Devoir de mathématiques, et corrigé, sur les pourcentages, probabilités, et tableaux de signe de deux fonctions et l'intersection de leurs courbes représentatives, posé en seconde générale, année scolaire 2023/2024
Exercice 1: Augmentation des salaires sur 3 ans
Le gouvernement a annoncé vouloir augmenter certains salaires de 10% en trois ans.
La première année, il augmente ces salaires de 5%, puis les réaugmente la deuxième année de 3%.
Cacher la correction
La première année, il augmente ces salaires de 5%, puis les réaugmente la deuxième année de 3%.
- À combien s'élève, après les deux premières années, un salaire initialement de 1500 euros ?
- Quel devrait être le pourcentage d'augmentation la troisième année pour que l'annonce faite soit respectée.
Correction exercice 1
- Après les deux premières années, le nouveau salaire sera de
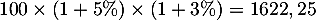 euros.
euros.
- Le gouvernement veut augmenter les salaires de 10% sur 3 ans, donc les multiplier par 1,1.
On note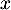 le pourcentage d'augmentation à appliquer la troisième année.
On multiplie donc par ailleurs ces salaires, avec les trois augmentations des trois années:
le pourcentage d'augmentation à appliquer la troisième année.
On multiplie donc par ailleurs ces salaires, avec les trois augmentations des trois années: 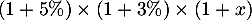 .
.
On doit donc avoir
![\[(1+5\%)(1+3\%)(1+x)=1,1
\iff 1+x=\dfrac{1,1}{1,05\tm1,03}\simeq 1,017\]](/Generateur-Devoirs/2nde/Chap10/ex4_c/4.png)
Ainsi, la troisième augmentation devra être d'environ 1,7%.
Cacher la correction
Exercice 2: Tableaux de signes et intersection de deux courbes
Soit 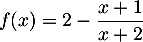 et
et 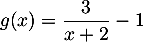 .
.
Cacher la correction
- Donner les tableaux de signe de
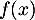 et de
et de 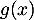 .
.
- Déterminer les coordonnées des éventuels points d'intersection des courbes de
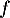 et de
et de 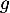 .
.
Correction exercice 2
- Sur le même dénominateur, on a
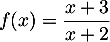 et
et 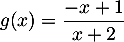 puis les tableaux de signe:
puis les tableaux de signe:
![\[\begin{tabular}[t]{|c|ccccccc|}\hline
$x$&$-\infty$ & & $-3$ & & $-2$ & & $+\infty$ \\\hline
$x+3$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ &\\\hline
$x+2$ & & $-$ & $|$ & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
$f(x)$ & & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} & $+$ & \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap3/exTSinter_c/3.png)
et
![\[\begin{tabular}[t]{|c|ccccccc|}\hline
$x$&$-\infty$ & & $-2$ & & $1$ & & $+\infty$ \\\hline
$-x+1$ & & $+$ & $|$ & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
$x+2$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ &\\\hline
$g(x)$ & & $-$ & \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
\end{tabular}\]](/Generateur-Devoirs/2nde/Chap3/exTSinter_c/4.png)
- Soit
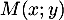 un éventuel point d'intersection des deux courbes,
alors
un éventuel point d'intersection des deux courbes,
alors 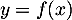 et
et 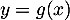 et donc en particulier
et donc en particulier
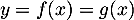 , c'est-à-dire avec les expressions précédentes,
, c'est-à-dire avec les expressions précédentes,
![\[\begin{array}{cll}&&\dfrac{x+3}{x+2}=\dfrac{-x+1}{x+2}\\[1em]
&\iff&\dfrac{x+3}{x+2}-\dfrac{-x+1}{x+2}=\dfrac{2x+2}{x+2}=0\enar\]](/Generateur-Devoirs/2nde/Chap3/exTSinter_c/9.png)
On a donc une équation quotient nulle, avec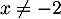 et
et 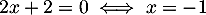 .
.
Enfin, pour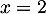 , l'ordonnée correspondante est
, l'ordonnée correspondante est
![\[y=f(-1)=g(-1)=2\]](/Generateur-Devoirs/2nde/Chap3/exTSinter_c/13.png)
Il y a donc un unique point d'intersection: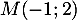
Cacher la correction
Exercice 3: Combinaisons avec un digicode
|
Le digicode ci-contre se trouve à l'entrée d'un immeuble. Un code se compose, dans cet ordre, de 2 lettres, puis 3 chiffres. Réaliser un arbre sommaire décrivant la situation et déterminer le nombre de codes possibles. |
![$$[t]{|c|c|c|}\hline
%\usepackage{colortbl}
\rowcolor[gray]{0.7}A & B & C \\\hline
1 & 2 & 3 \\\hline
4 & 5 & 6 \\\hline
7 & 8 & 9 \\\hline
$$](/Generateur-Devoirs/2nde/Chap9/exDigicode/1.png) |
Exercice 4: Allemand et/ou espagnol
Dans une classe de 30 élèves, 20 étudient l'allemand et 15 l'espagnol.
Dans cette classe 8 élèves étudient les deux langues.
On choisit un élève au hasard. On note les événements A:« l'élève étudie l'allemand» et E:« l’élève étudie l’espagnol».
Dans une classe de 30 élèves, 20 étudient l'allemand et 15 l'espagnol. Dans cette classe 8 élèves étudient les deux langues.
On choisit un élève au hasard. On note les événements A:« l'élève étudie l'anglais» et E:« l’élève étudie l'espagnol».
Cacher la correction
On choisit un élève au hasard. On note les événements A:« l'élève étudie l'allemand» et E:« l’élève étudie l’espagnol».
- Exprimer par une phrase les événements
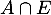 et
et 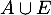 et donner leur probabilité.
et donner leur probabilité.
- Combien d'élèves n'apprennent ni l'allemand ni l'espagnol ?
Correction exercice 4
Dans une classe de 30 élèves, 20 étudient l'allemand et 15 l'espagnol. Dans cette classe 8 élèves étudient les deux langues.
On choisit un élève au hasard. On note les événements A:« l'élève étudie l'anglais» et E:« l’élève étudie l'espagnol».
-
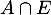 :« l'élève étudie les deux langues» et
:« l'élève étudie les deux langues» et 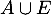 :« l'élève étudie au moins une des deux langues.
:« l'élève étudie au moins une des deux langues.
On a d'après l'énoncé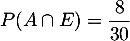 et
docn alors
et
docn alors
![\[\begin{array}{ll}P(A\cup E)&=P(A)+P(E)-P(A\cap E)\\[.6em]&=\dfrac{20}{30}+\dfrac{15}{30}-\dfrac8{30}\\[.6em]
&=\dfrac{27}{30}\enar\]](/Generateur-Devoirs/2nde/Chap9/exallesp_c/4.png)
- D'après le calcul précédent, on trouve que 3 élèves n'apprennent ni l'anglais ni l'espagnol.
Cacher la correction
Quelques autres devoirs
sur les équations, inéquations et tableaux de signes
sur les inéquations et tableaux de signes, et statistiques: moyenne, écart type, médianne et quartile, et représentation graphique par un diagramme en boîtes (ou boîtes à moustaches)
Statistiques: calculs de la moyenne et de l'écart type d'une série pondérée. Résolution d'inéquations. Ensemble de de définition de fonctions. Exercice complet sur les fonctions: sens de variation, courbe représentative et résolution graphique d'inéquations.
pourcentage et évolutions (taux global), résolution d'inéquations (tableaux de signes), et un problème complet avec des fonctions (bénéfice d'une société, rentabilité et bénéfice maximal)
pourcentage et probabilités, et deux tableaux de signes. Intersection de deux courbes
Quelques exercices corrigés
Exercices corrigés
Factorisations
Exercices corrigés
3 équations du 1er degré
Exercices corrigés
Factorisation, développement et résolution d'équations
Exercices corrigés
Vérification de la solution d'une équation - Calcul sur les radicaux et fractions
Exercices corrigés
Vérification de la solution d'une équation - Calcul sur les radicaux et fractions
Voir aussi:
![\[\begin{pspicture}(-1,-3.5)(12,6)
\psline(2,-3)(0,0)(2,3)
\psline(0,0)(2,0)
\rput(2.5,3){A}\rput(2.5,0){B}\rput(2.5,-3){C}
%
\psline(4.5,3)(3,3)(4.5,4)\psline(3,3)(4.5,2)
\rput(5,4){A}\rput(5,3){B}\rput(5,2){C}
%
\psline(7.5,4)(5.5,4)(7.5,5)
\rput(8,5){1}\rput(8,4.6){$\vdots$}\rput(8,4){9}
\psline(7.5,2.5)(5.5,3)(7.5,3.5)
\rput(8,3.5){1}\rput(8,3.1){$\vdots$}\rput(8,2.5){9}
\rput(6,2){\dots}
\psline(10,5)(8.5,5)(10,5.5)\rput(10.2,5.5){1}\rput(10.2,5.3){$\vdots$}
\psline(11.3,5.2)(10.4,5.5)(11.3,5.8)\rput(11.5,5.8){1}\rput(11.5,5.5){$\vdots$}
%
%%
\psline(4.5,0)(3,0)(4.5,1)\psline(3,0)(4.5,-1)
\rput(5,0){B}\rput(5,1){A}\rput(5,-1){C}
\psline(7.5,.5)(5.5,1)(7.5,1.5)
\rput(8,1.5){1}\rput(8,1){$\vdots$}\rput(8,.5){9}
%
\psline(3,-3)(4,-3)\rput(4.5,-3){\dots}
\end{pspicture}\]](/Generateur-Devoirs/2nde/Chap9/exDigicode_c/1.png)