Théorème de Rolle - Un contre exemple ?

Colle de mathématiques

Sujet de colle de maths:

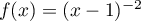Soit $f(x)=(x-1)^{-2}$ .
Montrer qu'il n'existe pas de solution à l'équation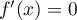

.
Vérifier que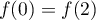

et préciser pourquoi cela ne contredit pas le théorème de Rolle.

Correction

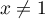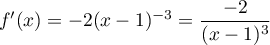On a, pour $x\not=1$ , $f'(x)=-2(x-1)^{-3}=\dfrac{-2}{(x-1)^3}$ et donc, en particulier, 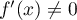$f'(x)\not=0$ pour tout 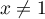$x\not=1$ et

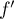(ni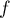

) n'est définie en

.
Ainsi, il n'existe pas de de solution à l'équation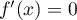

.

Cela ne contredit pas pour autant le théorème de Rolle car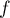

n'est pas continue (ni dérivable) sur

Autres sujets au hasard:

Voir aussi: