Intégrale impropre: convergence, calcul avec changement de variable
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
Énoncé du sujet
- Montrer que
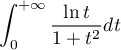 converge, puis,
en utilisant le changement de variables
converge, puis,
en utilisant le changement de variables 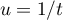 ,
montrer que
,
montrer que 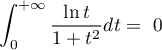 .
.
- Soit
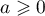 . Calculer
. Calculer 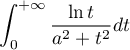 .
.
Correction
Correction
- La fonction
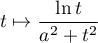 est continue sur
est continue sur
![$]0,+\infty[$](/Generateur-Devoirs/Colles/Integrale/exIIchgtvar1_c/2.png) . Au voisinage de 0, on a l'équivalence
. Au voisinage de 0, on a l'équivalence
![\[\dfrac{\ln t}{a^2+t^2}\sim \frac{\ln t}{a^2}\]](/Generateur-Devoirs/Colles/Integrale/exIIchgtvar1_c/3.png)
et on sait que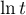 est intégrable en 0 (par exemple car
est intégrable en 0 (par exemple car
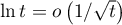 et que
et que 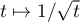 est
une intégrale de Riemann intégrable en 0, ou encore avec une primitive
est
une intégrale de Riemann intégrable en 0, ou encore avec une primitive 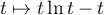 de
de 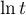 ).
De même, au voisinage de
).
De même, au voisinage de 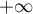 , on a
, on a
![\[\dfrac{\ln t}{a^2+t^2}=o\left(\frac{1}{t^{3/2}}\right)\]](/Generateur-Devoirs/Colles/Integrale/exIIchgtvar1_c/10.png)
On en déduit que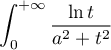 est convergente.
Le changement de variables
est convergente.
Le changement de variables 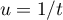 , qui est de classe
, qui est de classe 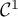 et strictement décroissant, donne ensuite
et strictement décroissant, donne ensuite
![\[\begin{array}{lcl}
I&=&\dsp\int_0^{+\infty}\frac{\ln t}{1+t^2}dt\\[1.4em]
&=&-\dsp\int_0^{+\infty}\frac{-\ln u}{1+\frac{1}{u^2}}\frac{-1}{u^2}du\\[1.4em]
&=&-\dsp\int_0^{+\infty}\frac{\ln u}{1+u^2}du=-I\enar\]](/Generateur-Devoirs/Colles/Integrale/exIIchgtvar1_c/14.png)
On en déduit que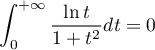 .
.
- On cherche bien sûr à se ramener à l'intégrale de la fonction précédente. Avec le changement de variables
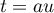 , on obtient
, on obtient
![\[\begin{array}{l}
\dsp\int_0^{+\infty}\dfrac{\ln t}{a^2+t^2}dt
=\dsp\int_0^{+\infty}\dfrac{\ln au}{a^2+a^2u^2}adu\\[1.5em]
\dsp\qquad=\int_0^{+\infty}\dfrac{\ln a}{a(1+u^2)}du
+\int_0^{+\infty}\frac{\ln u}{a(1+u^2)}du.\enar\]](/Generateur-Devoirs/Colles/Integrale/exIIchgtvar1_c/17.png)
De même que dans le calcul de la question précédente, et le fait qu'une primitive de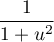 est
est 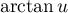 ,
on arrive alors
,
on arrive alors
![\[\int_0^{+\infty}\frac{\ln t}{a^2+t^2}dt=\frac{\pi\ln a}{2a}\]](/Generateur-Devoirs/Colles/Integrale/exIIchgtvar1_c/20.png)
Tag:Intégrale
Autres sujets au hasard:

Voir aussi: