Calcul d'intégrale avec changement de variable
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
Énoncé du sujet
Calculer 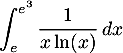 en utilisant le changement de variable
en utilisant le changement de variable 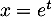
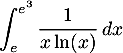 en utilisant le changement de variable
en utilisant le changement de variable Correction
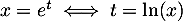 on obtient
on obtient 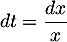 et alors
et alors
![\[\begin{array}{lcl}
I&=&\dsp\int_e^{e^3} \frac1{x\ln(x)}dx\\[1em]
&=&\dsp\int_1^3 \dfrac1t dt\\[1em]
&=&\Bigl[\ln(t)\Bigr]_1^3=\ln(3)
\enar\]](/Generateur-Devoirs/Colles/Integrale/exCchgt0_c/3.png)
Correction
Avec le changement de variable![\[\begin{array}{lcl}
I&=&\dsp\int_e^{e^3} \frac1{x\ln(x)}dx\\[1em]
&=&\dsp\int_1^3 \dfrac1t dt\\[1em]
&=&\Bigl[\ln(t)\Bigr]_1^3=\ln(3)
\enar\]](/Generateur-Devoirs/Colles/Integrale/exCchgt0_c/3.png)
Tag:Intégrale
Autres sujets au hasard:

Voir aussi: