Variations d'une fonction produit et racine carrée
Exercice corrigé - Spécialité maths, première générale
Énoncé
On considère la fonction 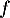 définie par l'expression
définie par l'expression
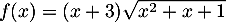 .
.
Après avoir précisé l'ensemble de définition de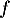 , déterminer le sens de variation de
, déterminer le sens de variation de 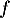 .
.
Après avoir précisé l'ensemble de définition de
Correction
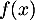 existe lorsque
existe lorsque 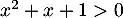 .
Ce trinôme du second degré a pour discriminant
.
Ce trinôme du second degré a pour discriminant 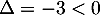 et n'adment donc aucune racine. On a ainsi le tableau de signe du trinôme
et n'adment donc aucune racine. On a ainsi le tableau de signe du trinôme
![\[\begin{tabular}{|c|cccc|}\hline
$x$ &$-\infty$ && $+\infty$&\\\hline
$x^2+x+1$&&$+$&&\\\hline\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exvarsqrt_c/4.png)
et la fonction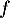 est donc définie sur
est donc définie sur 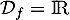 .
.
Le sens de variation de la fonction est donné par le signe de sa dérivée.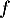 est un produit:
est un produit: 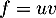 avec
avec
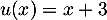 donc
donc 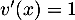 ,
et
,
et 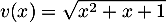 donc
donc 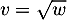 et alors
et alors
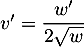 soit
soit
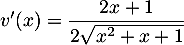 .
.
On dérive alors le produit: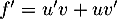 , soit
, soit
![\[f'(x)=\sqrt{x^2+x+1}+(x+3)\dfrac{2x+1}{2\sqrt{x^2+x+1}}\]](/Generateur-Devoirs/1S/Chap3/exvarsqrt_c/16.png)
qu'on réécrit sur un seul et même dénominateur
![\[\begin{array}{ll}f'(x)&=\dfrac{2\sqrt{x^2+x+1}^2+(x+3)(2x+1)}{2\sqrt{x^2+x+1}}\\[1em]
&=\dfrac{4x^2+9x+5}{2\sqrt{x^2+x+1}}
\enar\]](/Generateur-Devoirs/1S/Chap3/exvarsqrt_c/17.png)
On cherche maintenant le signe de cette expression. Le dénominateur est strictement positif, une racine carrée qui ne s'annule pas (comme on l'a montré au début de l'exercice).
Le numérateur est un trinôme du second degré, de discriminant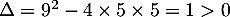 et admet donc deux racines réelles distinctes
et admet donc deux racines réelles distinctes
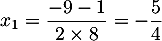 et
et 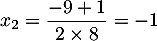 .
.
On dresse alors le tableau de signe de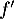 et de variation de
et de variation de 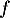 :
:
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-5/4$ && $-1$ && $+\infty$ \\\hline
$4x^2+9x+5$ && $+$ &0 & $-$ &0& $+$ & \\\hline
$2\sqrt{x^2+x+1}$ && $+$ &$|$&$+$ &$|$ & $+$ & \\\hline
$f'(x)$ && $+$ & 0 & $-$ & 0 & $+$ & \\\hline
&&&&&&&\\
$f(x)$ &&\psline{->}(-0.4,-0.3)(0.6,0.6)&&
\psline{->}(-0.4,0.6)(0.5,-0.3)&&
\psline{->}(-0.4,-0.3)(0.6,0.6)&\\
&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exvarsqrt_c/23.png)
Correction
et la fonction
Le sens de variation de la fonction est donné par le signe de sa dérivée.
On dérive alors le produit:
qu'on réécrit sur un seul et même dénominateur
![\[\begin{array}{ll}f'(x)&=\dfrac{2\sqrt{x^2+x+1}^2+(x+3)(2x+1)}{2\sqrt{x^2+x+1}}\\[1em]
&=\dfrac{4x^2+9x+5}{2\sqrt{x^2+x+1}}
\enar\]](/Generateur-Devoirs/1S/Chap3/exvarsqrt_c/17.png)
On cherche maintenant le signe de cette expression. Le dénominateur est strictement positif, une racine carrée qui ne s'annule pas (comme on l'a montré au début de l'exercice).
Le numérateur est un trinôme du second degré, de discriminant
On dresse alors le tableau de signe de
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-5/4$ && $-1$ && $+\infty$ \\\hline
$4x^2+9x+5$ && $+$ &0 & $-$ &0& $+$ & \\\hline
$2\sqrt{x^2+x+1}$ && $+$ &$|$&$+$ &$|$ & $+$ & \\\hline
$f'(x)$ && $+$ & 0 & $-$ & 0 & $+$ & \\\hline
&&&&&&&\\
$f(x)$ &&\psline{->}(-0.4,-0.3)(0.6,0.6)&&
\psline{->}(-0.4,0.6)(0.5,-0.3)&&
\psline{->}(-0.4,-0.3)(0.6,0.6)&\\
&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exvarsqrt_c/23.png)
Tag:Fonctions et dérivées
Voir aussi:
Quelques devoirs
second degré (équation et inéquation, tableau de signe). Dérivabilité d'une fonction en un point: taux d'accroissement et nombre dérivé (calcul et lecture graphique)
fonctions dérivées, étude de fonction et position relative de deux courbes
dérivées et étude de fonction. Angles en radians sur le cercle trigonométrique et en mesure principale
second degré, factorisation d'un polynome du 3ème degré. Calculs de fonctions dérivées et équation d'une tangente
Mesure principale d'un angle en radians - Etude des variations d'une fonctions - Etude d'une fonction auxilaire et TVI
