Suite définie par récurrence et suite intermédiaire géométrique
Exercice corrigé - Spécialité maths, première générale
Énoncé
On considère la suite  définie par son premier terme
définie par son premier terme
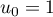 et par la relation, pour tout entier naturel
et par la relation, pour tout entier naturel 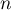 ,
,
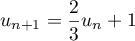 .
.
- Calculer
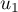 et
et  .
.
- Montrer que
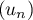 n'est ni arithmétique, ni géométrique.
n'est ni arithmétique, ni géométrique.
- On pose, pour tout entier naturel
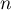 ,
,
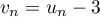 .
.
- Montrer que
 est une suite géométrique,
dont on précisera le premier terme et la raison.
est une suite géométrique,
dont on précisera le premier terme et la raison.
- Exprimer
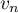 en fonction de
en fonction de 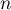 .
.
- En déduire l'expression de
 en fonction de
en fonction de 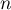 .
.
- Montrer que
Correction
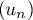 définie par son premier terme
définie par son premier terme
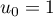 et par la relation, pour tout entier naturel
et par la relation, pour tout entier naturel  ,
,
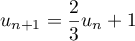 .
.
Correction
On considère la suite-
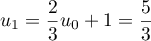 et
et 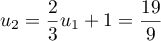 .
.
- On a
 donc
donc  n'est pas arithmétique.
n'est pas arithmétique.
De même, donc
donc  n'est pas géométrique non plus.
n'est pas géométrique non plus.
- On pose, pour tout entier naturel
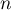 ,
,
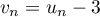 .
.
- Pour tout entier
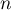 ,
,
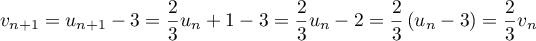 .
.
Ainsi, est une suite géométrique de raison
est une suite géométrique de raison 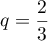 et de premier terme
et de premier terme 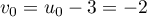 .
.
- On en déduit que, pour tout entier
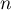 ,
,
 .
.
- On obtient alors,
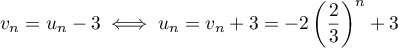 .
.
- Pour tout entier
Tag:Suites
Voir aussi:
Quelques devoirs
variation d'une fonction composée avec une exponentielle - Deux inéquations avec des exponentielles - Suite numériques explicite et récurrente, construction graphique des premiers termes
Suites: construction graphique des premiers termes, suite intermédiaire arithmétique - Etude d'une suite récurrente avec une suite auxiliaire arithmétique
sur les suites: sommes des termes d'une suite arithmétique et géométrique. Etude d'une suite récurrente avec une suite auxiliaire. Suite récurrente définie avec une fonction exponentielle. Balle rebondissante: hauteur des rebonds et distance totales parcourue
fin d'année, sur les fonctions, exponentielle, suite et variable aléatoire
