Jeu dans une urne et 2nd degré
Exercice corrigé - Spécialité maths, première générale
Énoncé
Une urne contient 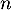 boules: une boule rouge et
boules: une boule rouge et  boules blanches.
boules blanches.
On tire successivement et avec remise deux boules dans l'urne.
On tire successivement et avec remise deux boules dans l'urne.
- Exprimer en fonction de
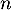 la probabilité des événements suivants:
la probabilité des événements suivants:
- M: "Les deux boules sont de la même couleur"
- N: "Les deux boules sont de couleurs différentes"
- On considère le jeu suivant:
le joueur perd
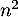 euros si M est réalisé
et gagne
euros si M est réalisé
et gagne 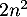 euros sinon.
euros sinon.
On appelle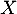 la variable aléatoire égale au gain algébrique
(positif ou négatif) du joueur.
la variable aléatoire égale au gain algébrique
(positif ou négatif) du joueur.
- Déterminer la loi de probabilité de
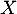 .
.
- Démontrer que
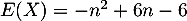 .
.
- Pour quelles valeurs de
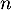 le jeu est-il favorable au joueur ?
le jeu est-il favorable au joueur ?
- Si on laisse le choix au joueur, quel nombre de boules blanches doit-il choisir ?
- Déterminer la loi de probabilité de
Correction
Correction
-
![\[\psset{xunit=1cm,yunit=.5cm}
\begin{pspicture}(-2,-4.2)(5,2.6)
\psline(0,0)(1.5,1.5)\rput(1.75,1.5){$R$}
\rput(0.6,1.5){\small $\frac{1}{n}$}
\psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$R$}
\rput(2.8,2.6){\small $\frac{1}{n}$}
\psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$B$}
\rput(2.8,0.3){\small $\frac{n-1}{n}$}
%
\psline(0,0)(1.5,-2.5)\rput(1.75,-2.5){$B$}
\rput(.6,-2){\small $\frac{n-1}{n}$}
\psline(2,-2.5)(3.5,-1.75)\rput(3.75,-1.75){$R$}
\rput(2.8,-1.5){\small $\frac{1}{n}$}
\psline(2,-2.5)(3.5,-3.25)\rput(3.75,-3.25){$B$}
\rput(2.8,-3.7){\small $\frac{n-1}{n}$}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap7/exurne_c/1.png)
On a alors les probabilités:
![\[P(M)=\lp\dfrac1n\rp^2+\lp\dfrac{n-1}{n}\rp^2
=\dfrac{n^2-2n+2}{n^2}\]](/Generateur-Devoirs/1S/Chap7/exurne_c/2.png)
et
![\[P(N)=2\tm\dfrac1n\tm\dfrac{n-1}{n}=\dfrac{2(n-1)}{n^2}\]](/Generateur-Devoirs/1S/Chap7/exurne_c/3.png)
-
- La loi de probabilité de
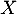 est
est
![\[\begin{tabular}{|c|c|c|}\hline
Valeurs de $X$: $x_i$ & $-n^2$ & $2n^2$
\\\hline
$P\left( X=x_i\rp$ & $\dfrac{n^2-2n+2}{n^2}$ & $\dfrac{2(n-1)}{n^2}$
\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap7/exurne_c/5.png)
-
![\[E(X)
=-n^2\tm\dfrac{n^2-2n+2}{n^2}+2n^2\tm\dfrac{2(n-1)}{n^2}
=-n^2+6n-6\]](/Generateur-Devoirs/1S/Chap7/exurne_c/6.png)
- Le jeu est favorable au joueur lorsque
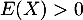 .
.
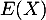 est un trinôme du second degré de discriminant
est un trinôme du second degré de discriminant
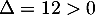 et admet deux racines
et admet deux racines
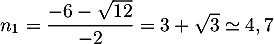 et
et
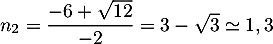 .
.
On a alors![$E(X)>0\iff n\in]n_1;n_2[$](/Generateur-Devoirs/1S/Chap7/exurne_c/12.png) , soit
pour
, soit
pour  ,
,  ou
ou  , donc pour
1, 2 ou 3 boules blanches.
, donc pour
1, 2 ou 3 boules blanches.
-
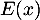 est un trinôme du second degré dont le maximum est atteint
en
est un trinôme du second degré dont le maximum est atteint
en 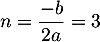 , pour lequel
, pour lequel 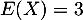 .
.
Le joueur a donc tout intérêt a choisir que l'urne contienne 2 boules blanches, pour un gain moyen maximal de 3 euros.
- La loi de probabilité de
Tags:Variables aléatoires2nd degré
Voir aussi:
