Etude de fonction, avec fonction auxiliaire
Exercice corrigé - Spécialité maths, première générale
Énoncé
- On appelle
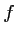 la fonction définie sur
la fonction définie sur
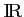 par l'expression
par l'expression
 .
.
- a. Etudier les variations de
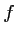 , et dresser son tableau de
variation.
, et dresser son tableau de
variation.
- b. Montrer que l'équation
 a une unique solution
a une unique solution 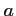 sur
sur
![$ [2;3]$](/Generateur-Devoirs/1S/Chap3/ex3_img6.png) .
.
Donner un encadrement de
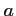 d'amplitude
d'amplitude 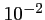 .
.
- c. Déterminer le signe de
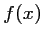 sur
sur
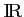 .
.
- a. Etudier les variations de
- On appelle
 la fonction définie sur
la fonction définie sur
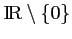 par
par
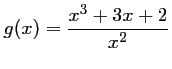 .
.
- a. Calculer la dérivée
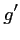 de
de  et montrer que
et montrer que
 pour tout
pour tout 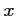 de
de
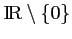 .
.
- b. En déduire les variations de
 .
.
- a. Calculer la dérivée
Correction
Correction
- On appelle
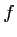 la fonction définie sur
la fonction définie sur
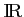 par l'expression
par l'expression
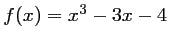 .
.
- a.
-
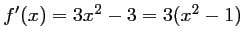 , et donc,
, et donc,
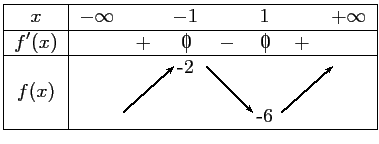
- b.
- La fonction
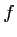 est dérivable sur
est dérivable sur ![$ [2;3]$](/Generateur-Devoirs/1S/Chap3/ex3_c_img6.png) ,
strictement croissante, et telle que
,
strictement croissante, et telle que 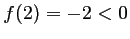 et
et 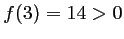 .
.
On en déduit, d'après le théorème des valeurs intermédiares, que l'équation
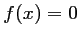 admet une unique solution sur
admet une unique solution sur ![$ [2;3]$](/Generateur-Devoirs/1S/Chap3/ex3_c_img6.png) .
.
De plus, on calcule que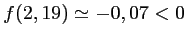 et
et
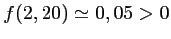 , d'où
, d'où
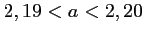 .
.
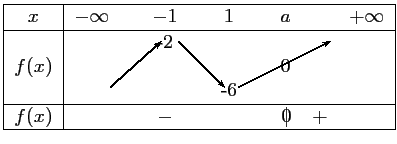
- c.
- On en déduit le signe de
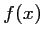 sur
sur
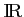 :
:
- On appelle
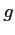 la fonction définie sur
la fonction définie sur
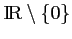 par
par
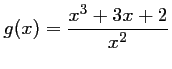 .
.
- a.
- On a
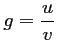 , avec
, avec
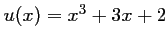 ,
,
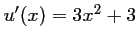 , et
, et
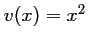 ,
, 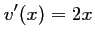 , d'où,
, d'où,
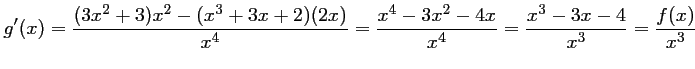
- b.
- On déduit de la question 1.c) le tableau de variation:
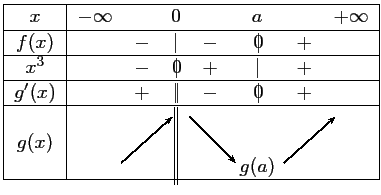
Tag:Fonctions et dérivées
Voir aussi:
