Egalité de sinus
Exercice corrigé - Spécialité maths, première générale
Énoncé
Résoudre l'équation suivante dans
 :
:
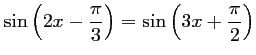 .
.
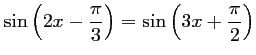 .
.
Correction
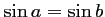 équivaut à :
équivaut à :
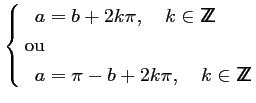
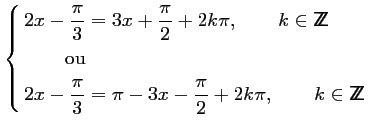
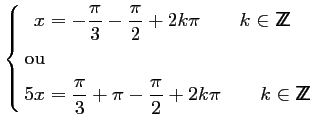
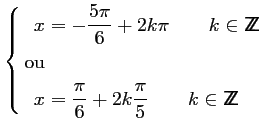
Correction
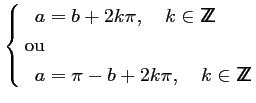
soit ici,
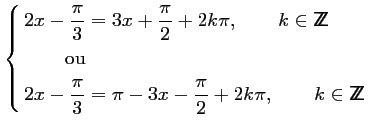
On obtient donc les deux solutions :
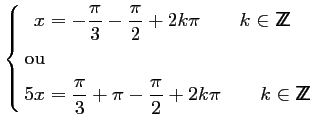
soit encore :
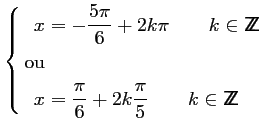
ce qui donne l'ensemble des solutions.
Tag:Trigonométrie
Voir aussi:
Quelques devoirs
dérivées et étude de fonction. Angles en radians sur le cercle trigonométrique et en mesure principale
Géométrie avec le produit scalaire, projeté orthogonal et calcul d'un angle et droites tangentes à une parabole perpendiculaires
Mesure principale d'un angle en radians - Etude des variations d'une fonctions - Etude d'une fonction auxilaire et TVI
