Suites imbriquées et diagonalisation
Exercice corrigé - Maths expertes, terminale générale
Énoncé
On considère les suites 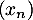 et
et 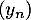 définies par les relations de récurrence, pour tout entier naturel
définies par les relations de récurrence, pour tout entier naturel 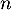 ,
,
![\[\la\begin{array}{ll}x_{n+1}&=y_n\\y_{n+1}&=-\dfrac12x_n+\dfrac32y_n\enar\right.\]](/Generateur-Devoirs/Mex/Matrices/exsuites/4.png)
sachant que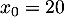 et
et 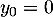 .
.
On note de plus les matrice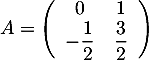 et
et
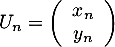 , pour tout entier naturel
, pour tout entier naturel 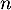 .
.
![\[\la\begin{array}{ll}x_{n+1}&=y_n\\y_{n+1}&=-\dfrac12x_n+\dfrac32y_n\enar\right.\]](/Generateur-Devoirs/Mex/Matrices/exsuites/4.png)
sachant que
On note de plus les matrice
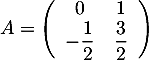 et
et
- Calculer
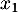 et
et 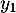 puis
puis 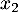 et
et 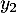 .
.
- Exprimer matriciellement la relation de récurrence définissant les suites
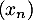 et
et 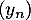 à l'aide de la matrice
à l'aide de la matrice 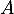 .
.
- Soit
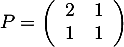 .
.
Calculer la matrice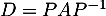 .
.
- Donner
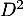 et
et 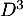 puis la matrice
puis la matrice 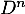 (sans justification supplémentaire).
(sans justification supplémentaire).
En déduire l'expression de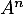 en fonction de
en fonction de 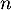 et des matrices
et des matrices 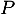 et
et 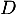 , puis calculer la matrice
, puis calculer la matrice 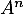 explicitement en fonction de
explicitement en fonction de 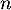 .
.
- Donner alors l'expression de
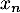 et
et 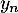 en fonction de
en fonction de 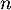 .
.
Quelle sont les limites de ces deux suites ?
Correction
Correction
- On a
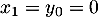 et
et 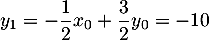
puis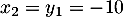 et
et 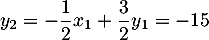
- Les relations de récurrence s'expriment matriciellement par
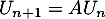 .
.
- On calcule tout d'abord la matrice inverse, car qui existe bien car
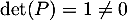 , et donc
, et donc
![\[P^{-1}=\dfrac1{\det(P)}\lp\begin{array}{cc}1&-1\\-1&2\enar\rp=\lp\begin{array}{cc}1&-1\\-1&2\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exsuites_c/7.png)
et on calcule alors les deux produits matriciels successifs:
![\[D=PAP^{-1}
=\lp\begin{array}{cc}\dfrac12&0\\0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exsuites_c/8.png)
- On calcule
![\[D^2=\lp\begin{array}{cc}\dfrac12&0\\0&1\enar\rp\lp\begin{array}{cc}\dfrac12&0\\0&1\enar\rp
=\lp\begin{array}{cc}\lp\dfrac12\rp^2&0\\0&1^2\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exsuites_c/9.png)
puis
![\[\begin{array}{ll}D^3&=D^2D\\
&=\lp\begin{array}{cc}\lp\dfrac12\rp^2&0\\0&1\enar\rp\lp\begin{array}{cc}\dfrac12&0\\0&1\enar\rp\\[2em]
&=\lp\begin{array}{cc}\lp\dfrac12\rp^3&0\\0&1^3\enar\rp\enar\]](/Generateur-Devoirs/Mex/Matrices/exsuites_c/10.png)
qu'on généralise à
![\[D^n=\lp\begin{array}{cc}\lp\dfrac12\rp^n&0\\0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exsuites_c/11.png)
On en déduit que
![\[\begin{array}{ll}A^n&=\underbrace{A\,A\,A\,\dots\,A}_{n \text{termes}}\\[1.6em]
&=PA\underbrace{P^{-1}P}_{=I_2}D\underbrace{P^{-1}P}_{=I_2}DP{-1}\dots\,\underbrace{P^{-1}P}_{=I_2}DP^{-1}\\[1.6em]
&=PD^nP^{-1}
\enar\]](/Generateur-Devoirs/Mex/Matrices/exsuites_c/12.png)
On calcule enfin explicitement cette matrice:
![\[\begin{array}{ll}A^n&=PD^nP^{-1}\\
&=\lp\begin{array}{cc}2&1\\1&1\enar\rp\lp\begin{array}{cc}\lp\dfrac12\rp^n&0\\0&1\enar\rp P^{-1}\\
&=\lp\begin{array}{cc}2\lp\dfrac12\rp^n&1\\\lp\dfrac12\rp^n&1\enar\rp\lp\begin{array}{cc}1&-1\\-1&2\enar\rp\\[3em]
&=\lp\begin{array}{cc}2\lp\dfrac12\rp^n-1&-2\lp\dfrac12\rp^n+2\\\lp\dfrac12\rp^n-1&-\lp\dfrac12\rp^n+2\enar\rp
\enar\]](/Generateur-Devoirs/Mex/Matrices/exsuites_c/13.png)
- On a
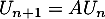 , pour tout entier
, pour tout entier 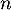 , et donc
, et donc 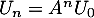 , soit
, soit
![\[\lp\begin{array}{c}x_n\\y_n\enar\rp=A^n\lp\begin{array}{c}x_0\\y_0\enar\rp
=A^n\lp\begin{array}{c}20\\0\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exsuites_c/17.png)
et alors, avec l'expression trouvée à la question précédente,
![\[\la\begin{array}{ll}x_n&=20\lp2\lp\dfrac12\rp^n-1\rp\\[1.4em]
y_n&=20\lp\lp\dfrac12\rp^n-1\rp
\enar\right.\]](/Generateur-Devoirs/Mex/Matrices/exsuites_c/18.png)
Comme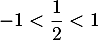 on a
on a 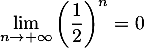 ,
et donc on trouve finalement
,
et donc on trouve finalement
![\[\lim_{n\to+\infty}x_n=\lim_{n\to+\infty}y_n=-20\]](/Generateur-Devoirs/Mex/Matrices/exsuites_c/21.png)
Tag:matrices
Voir aussi:
Quelques devoirs
sur les matrices et calcul matriciel, produit, puissance d'une matrice, définition de l'inverse d'une matrice
sur la factorisation et racines d'un polynôme complexe et matrices et calcul matriciel, diagonalisation et limites de suites
sur binôme de Newton et les racines de l'unité. Calcul de la puissance n-ième d'une matrice
sur les matrices, calcul matriciel et les nombres complexes: géométrie, formes algébriques et exponentielles.
