Suites: annales de bac et corrections
Terminale générale, spécialité mathématiques
Annales de bac: sujets et corrigés d'exercices posés au baccalauréat en mathématiques sur les suites: suites récurrentes, limites, graphique, suites arithmétiques et géométriques et sommes des premiers termes
Exercice 1: Bac 2023 - Suite géométrique, exponentielle et Python
Une entreprise a créé une Foire Aux Questions (« FAQ ») sur son site internet.
On étudie le nombre de questions qui y sont posées chaque mois.
Partie A : Première modélisation
Dans cette partie, on admet que, chaque mois :
Au cours du premier mois,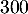 questions ont été posées.
questions ont été posées.
Pour estimer le nombre de questions, en centaines, présentes sur la FAQ le n-ième mois, on modélise la situation ci-dessus à l'aide de la suite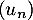 définie par :
définie par : 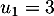 et, pour tout entier naturel
et, pour tout entier naturel 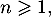
![\[u_{n+1} = 0,9u_n + 1,3\]](/Generateur-Devoirs/TS/ChapSuites/exBac200323/7.png)
Partie B : Une autre modélisation
Dans cette partie, on considère une seconde modélisation à l'aide d'une nouvelle suite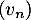 définie pour tout entier naturel
définie pour tout entier naturel 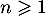 par:
par:
![\[v_n = 9 - 6 \times e^{-0,19\times(n - 1)}.\]](/Generateur-Devoirs/TS/ChapSuites/exBac200323/16.png)
Le terme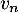 est une estimation du nombre de questions, en centaines, présentes le
est une estimation du nombre de questions, en centaines, présentes le 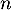 -ième mois sur la FAQ.
-ième mois sur la FAQ.
Partie C : Comparaison des deux modèles
Partie A : Première modélisation
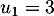 et, pour tout entier naturel
et, pour tout entier naturel  ,
, 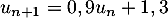
Partie B : Une autre modélisation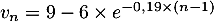 pour tout entier naturel
pour tout entier naturel  .
.
Partie C : Comparaison des deux modèles
Cacher la correction
On étudie le nombre de questions qui y sont posées chaque mois.
Partie A : Première modélisation
Dans cette partie, on admet que, chaque mois :
- 90 % des questions déjà posées le mois précédent sont conservées sur la FAQ ;
- 130 nouvelles questions sont ajoutées à la FAQ.
Au cours du premier mois,
Pour estimer le nombre de questions, en centaines, présentes sur la FAQ le n-ième mois, on modélise la situation ci-dessus à l'aide de la suite
- Calculer
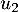 et
et  et proposer une interprétation dans le contexte de l'exercice.
et proposer une interprétation dans le contexte de l'exercice.
- Montrer par récurrence que pour tout entier naturel
 :
:
![\[u_n = 13 - \dfrac{100}{9} \times 0,9^n.\]](/Generateur-Devoirs/TS/ChapSuites/exBac200323/11.png)
- En déduire que la suite
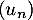 est croissante.
est croissante.
|
4. On considère le programme ci-contre, écrit en langage Python.
Déterminer la valeur renvoyée par la saisie de seuil(8.5) et l'interpréter dans le contexte de l'exercice. |
![\[\renewcommand\arraystretch{0.9}
\begin{tabular}{|p{5cm}|} \hline
def seuil(p) :\\
\qquad n=1\\
\qquad u=3\\
\qquad while u$<=$p :\\
\qquad \qquad n=n+1\\
\qquad \qquad u=0.9*u+1.3 \\
\qquad return n\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/exBac200323/13.png) |
Partie B : Une autre modélisation
Dans cette partie, on considère une seconde modélisation à l'aide d'une nouvelle suite
Le terme
- Préciser les valeurs arrondies au centième de
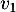 et
et  .
.
- Déterminer, en justifiant la réponse, la plus petite valeur de
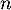 telle que
telle que  .
.
Partie C : Comparaison des deux modèles
- L'entreprise considère qu'elle doit modifier la présentation de son site lorsque plus de 850 questions sont présentes sur la FAQ.
Parmi ces deux modélisations, laquelle conduit à procéder le plus tôt à cette modification ?
Justifier votre réponse. - En justifiant la réponse, pour quelle modélisation y a-t-il le plus grand nombre de questions sur la FAQ à long terme?
Correction exercice 1
Partie A : Première modélisation
-
 , soit 400 questions au bout de 1 mois
et
, soit 400 questions au bout de 1 mois
et 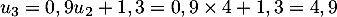 , soit 490 questions au bout du 2ème mois.
, soit 490 questions au bout du 2ème mois.
- Soit
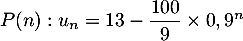 , pour
, pour  .
.
Initialisation: Pour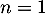 on a
on a
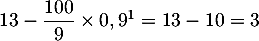 ,
et comme
,
et comme 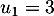 , on en déduit que la propriété
, on en déduit que la propriété  est donc vraie.
est donc vraie.
Hérédité: Supposonss que, pour un certain entier , la propriété
, la propriété  soit vraie, c'est-à-dire:
soit vraie, c'est-à-dire:
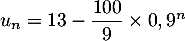 .
.
On a, par définition de la suite,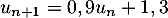 ,
et donc, en utilisant l'hypothèse de récurrence,
,
et donc, en utilisant l'hypothèse de récurrence,
![\[\begin{array}{ll}
u_{n+1}&=0,9\tm\lp13 - \dfrac{100}9\tm0,9^n\rp+1,3\\
&=0,9\tm13-\dfrac{100}9\tm0,9^{n+1}+1,3\\
&=13-\dfrac{100}9\tm0,9^{n+1}\enar\]](/Generateur-Devoirs/TS/ChapSuites/exBac200323_c/16.png)
ce qui montre que la propriété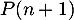 est donc aussi vraie.
est donc aussi vraie.
Conclusion: On vient donc de démontrer, d'après le principe de récurrence, que
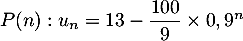 est vraie pour tout entier
est vraie pour tout entier  .
.
- En utilisant l'expression précédente, on a
![\[\begin{array}{ll}
u_{n+1}-u_n&=\lp13 - \dfrac{100}9\tm0,9^{n+1}\rp-\lp13 - \dfrac{100}9\tm0,9^n\rp\\[1em]
&=13 - \dfrac{100}9\tm0,9^{n+1}-13 + \dfrac{100}9\tm0,9^n\\[.8em]
&=\dfrac{100}9\tm0,9^n\lp0,9-1\rp\\[.8em]
&=\dfrac{100}9\tm0,9^n\tm0,1>0\enar\]](/Generateur-Devoirs/TS/ChapSuites/exBac200323_c/20.png)
On en déduit que la suite est croissante.
est croissante.
- Ce programme retourne le premier rang
 tel que
tel que  .
.
On trouve, soit en effectuant ce programme sur la calculatrice, soit par le calcul exact:
![\[\begin{array}{ll}
u_n>8,5 &\iff 13-\dfrac{100}9\tm0,9^n>8,5\\
&\iff -\dfrac{100}9\tm0,9^n>-4,5\\
&\iff 0,9^n<\dfrac{4,5\tm9}{100}\\
&\iff\ln(0,9^n)=n\ln(0,9)<\ln\lp\dfrac{4,5\tm9}{100}\rp\\
&\iff n>\dfrac1{ln(0,9)}\tm\dfrac{4,5\tm9}{100}\simeq8,58
\enar\]](/Generateur-Devoirs/TS/ChapSuites/exBac200323_c/24.png)
Ainsi, le premier entier, renvoyé par le programme Python lors de l'exécution de seuil(8.5) est .
.
Partie B : Une autre modélisation
-
 et
et 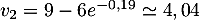 .
.
-
![\[\begin{array}{ll}v_n > 8,5
&\iff 9 - 6 \times e^{-0,19\times(n-1)}>8,5 \\
&\iff - 6 \times e^{-0,19\times(n-1)}>-0,5\\
&\iff e^{-0,19(n-1)}<\dfrac{0,5}{6}\\
&\iff -0,19(n-1)<\ln\lp\dfrac{0,5}{6}\rp\\[1em]
&\iff n-1>\dfrac1{-0,19}\tm\ln\lp\dfrac{0,5}{6}\rp\\[1em]
&\iff n>\dfrac1{-0,19}\tm\ln\lp\dfrac{0,5}{6}\rp+1\simeq 14,08
\enar\]](/Generateur-Devoirs/TS/ChapSuites/exBac200323_c/30.png)
La plus petite valeur entière recherchée est donc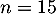 .
.
Partie C : Comparaison des deux modèles
- Avec le premier modèle, les 850 questions sont dépassées pour
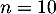 semaines, tandis qu'avec le deuxième modèle, elles sont dépassées pour
semaines, tandis qu'avec le deuxième modèle, elles sont dépassées pour 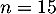 semaines.
Le premier modèle conduit donc à procéder le plus tôt à la modification.
semaines.
Le premier modèle conduit donc à procéder le plus tôt à la modification.
- A long terme, c'est-à-dire pour
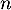 grand, ou encore pour
grand, ou encore pour
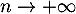 , on a:
, on a:
- Pour le 1er modèle: comme
 , on a
, on a
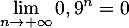 et donc
et donc

- Pour le 2ème modèle: on a
 et donc
et donc
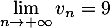
À long terme, pour la première modélisation il y a le plus grand nombre de questions sur la FAQ à long terme. - Pour le 1er modèle: comme
Cacher la correction
Exercice 2: Bac 2022 - Exponentielle et suite récurrente
Dans le cadre d'un essai clinique on envisage deux protocoles de traiterment de
d'une maladie.
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en mg, par la fonction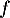 définie sur l'intervalle [0 ; 10] par
définie sur l'intervalle [0 ; 10] par
![\[f(t) = 3t e^{-0,5t+1},\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022/2.png)
où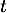 désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqüre intraveineuse, une dose de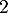 mg de médicament puis à réinjecter toutes les heures une dose de
mg de médicament puis à réinjecter toutes les heures une dose de  mg.
mg.
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de 30 % par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite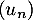 où, pour tout entier naturel
où, pour tout entier naturel 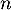 ,
,  désigne la quantité de médicament, exprimée en mg, présente dans le sang du patient immédiatement après l'injection de la
désigne la quantité de médicament, exprimée en mg, présente dans le sang du patient immédiatement après l'injection de la 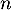 -ième heure. On a donc
-ième heure. On a donc  .
.
Partie A : Étude du premier protocole
Partie B : Étude du deuxième protocole
Cacher la correction
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en mg, par la fonction
où
-
- On admet que la fonction
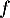 est dérivable sur l'intervalle [0 ; 10] et on note
est dérivable sur l'intervalle [0 ; 10] et on note 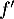 sa fonction dérivée.
Montrer que, pour tout nombre réel
sa fonction dérivée.
Montrer que, pour tout nombre réel  de [0 ; 10], on a:
de [0 ; 10], on a: 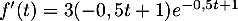 .
.
- En déduire le tableau de variations de la fonction
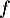 sur l'intervalle [0 ; 10].
sur l'intervalle [0 ; 10].
- Selon cette modélisation, au bout de combien de temps la quantité de médicament présente dans le sang du patient sera-t-elle maximale ? Quelle est alors cette quantité maximale?
- On admet que la fonction
-
- Montrer que l'équation
 admet une unique solution sur l'intervalle [0 ; 2] notée
admet une unique solution sur l'intervalle [0 ; 2] notée 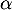 , dont on donnera une valeur approchée à
, dont on donnera une valeur approchée à 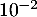 près.
On admet que l'équation
près.
On admet que l'équation 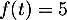 admet une unique solution sur l'intervalle [2 ; 10], notée
admet une unique solution sur l'intervalle [2 ; 10], notée  , et qu'une valeur approchée de
, et qu'une valeur approchée de  à
à  près est 3,46.
près est 3,46.
- On considère que ce traitement est efficace lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à 5 mg. Déterminer, à la minute près, la durée d'efficacité du médicament dans le cas de ce protocole.
- Montrer que l'équation
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqüre intraveineuse, une dose de
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de 30 % par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite
- Calculer, selon cette modélisation, la quantité
 , de médicament (en mg) présente dans le sang du patient immédiatement après l'injection de la première heure.
, de médicament (en mg) présente dans le sang du patient immédiatement après l'injection de la première heure.
- Justifier que, pour tout entier naturel
 , on a :
, on a : 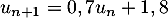 .
.
-
- Montrer par récurrence que, pour tout entier naturel
 , on a :
, on a : 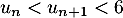 .
.
- En déduire que la suite
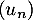 est convergente. On note
est convergente. On note 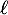 sa limite.
sa limite.
- Déterminer la valeur de
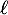 . Interpréter cette valeur dans le contexte de l'exercice.
. Interpréter cette valeur dans le contexte de l'exercice.
- Montrer par récurrence que, pour tout entier naturel
- On considère la suite
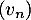 définie, pour tout entier naturel
définie, pour tout entier naturel  , par
, par 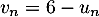 .
.
- Montrer que la suite
 est une suite géométrique de raison
est une suite géométrique de raison  dont on précisera le premier terme.
dont on précisera le premier terme.
- Déterminer l'expression de
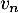 en fonction de
en fonction de 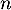 , puis de
, puis de 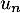 n en fonction de
n en fonction de 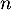 .
.
- Avec ce protocole, on arrête les injections lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à 5,5 mg. Déterminer, en détaillant les calculs, le nombre d'injections réalisées en appliquant ce protocole.
- Montrer que la suite
Correction exercice 2
Partie A : Étude du premier protocole
-
- On a
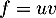 avec
avec 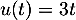 donc
donc 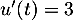 et
et 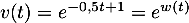 avec
avec
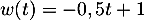 donc
donc 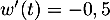 et alors
et alors 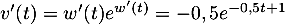 .
.
On obtient alors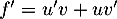 , soit
, soit
![\[\begin{array}{ll}f'(t)&=3e^{-0,5t+1}+3t\tm\lp-0,5e^{-0,5t+1}\rp\\[.4em]
&=3e^{-0,5t+1}\lp1-0,5t\rp\\[.4em]
&=3(-0,5t + 1)e^{-0,5t+1}\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/9.png)
- On a alors le signe de lé dérivée et le sens de variation:
![\[\begin{tabular}{|c|*5c|}\hline
$t$ & 0 && 2 && 10 \\\hline
$-0,5t+1$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
$e^{-0,5t+1}$ && $+$ &\vline & $+$ & \\\hline
$f'(t)$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/10.png)
- Selon cette modélisation, la quantité maximale de médicament présente dans le sang du patient sera de
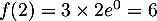 mg, au bout de 2 heures.
mg, au bout de 2 heures.
- On a
-
- Sur [0;2], la fonction
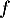 est continue (car même dérivable),
strictement croissante, avec
est continue (car même dérivable),
strictement croissante, avec 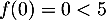 et
et  ,
et ainsi, d'après le théorème des valeurs intermédiaires
(théorème de la bijection), on sait donc qu'il existe une unique
solution
,
et ainsi, d'après le théorème des valeurs intermédiaires
(théorème de la bijection), on sait donc qu'il existe une unique
solution 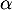 à l'équation
à l'équation 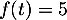 .
.
Avec la calculatrice, par balayage par exemple, on touve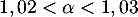 soit,
soit, 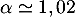 .
.
- On peut compléter le tableau de variation:
![\[\begin{tabular}{|c|*9c|}\hline
$t$ & 0 &&$\alpha$ && 2 &&$\beta$&& 10 \\\hline
&&&&&&&&&\\
$f$&&\psline[arrowsize=8pt]{->}(-.5,-.5)(1.3,.5)&5&&&
\psline[arrowsize=8pt]{->}(-.2,.5)(1.4,-.5)&5&&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/19.png)
grâce auquel on trouve que la durée d'efficacité du médicament est donc de soit 2,44 heures, ou encore 2 heures et 26 minutes.
soit 2,44 heures, ou encore 2 heures et 26 minutes.
- Sur [0;2], la fonction
Partie B : Étude du deuxième protocole
- Selon cette modélisation, à la première heure la quantité dans le sang a diminué de 30%, il en reste donc
 .
On réinjecte de plus une nouvelle dose de 1,8 mg, et on trouve donc que
.
On réinjecte de plus une nouvelle dose de 1,8 mg, et on trouve donc que
![\[u_1=0,7\tm2+1,8=3,2\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/22.png)
- De même que précédemment, à la (n+1)-ème heure,
la quantité dans le sang présente l'heure précédente, soit
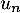 a diminué de 30%, soit
a diminué de 30%, soit 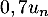 , et on réinjecte, donc ajoute, 1,8 mg.
, et on réinjecte, donc ajoute, 1,8 mg.
On obtient donc bien la relation .
.
-
- Soit la proposition
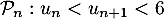 .
.
Initialisation: on a et
et 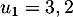 d'où
d'où
 est vraie:
est vraie:  .
.
Hérédité: Supposons que pour un certain entier ,
,
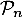 soit vraie, c'est-à-dire
soit vraie, c'est-à-dire
 .
.
Alors, en multipliant par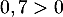 , on obtient
, on obtient
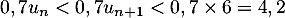 ,
,
puis en ajoutant 1,8 on aboutit à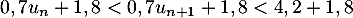 ,
,
c'est-à-dire exactement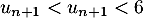 et qui montre donc
et qui montre donc 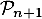 est alors vraie.
est alors vraie.
Conclusion: on vient donc de démontrer, d'après le principe de récurrence, que pour tout entier ,
,
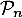 est vraie, c'est-à-dire
est vraie, c'est-à-dire 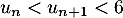 .
.
- On déduit du résultat précédent que la suite
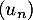 est croissante et aussi qu'elle est majorée par 6.
est croissante et aussi qu'elle est majorée par 6.
On en déduit donc (théorème de convergence monotone) qu'elle converge vers une limite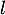 .
.
- On a
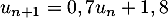 et on sait que
et on sait que  .
.
Ainsi, on doit nécessairement avoir (théorème du point fixe), que
![\[l=0,7l+1,8\iff l=\dfrac{1,8}{0,3}=6\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/46.png)
- Soit la proposition
-
- Pour tout entier
 , on a
, on a
![\[\begin{array}{ll}v_{n+1}&=6-u_{n+1}\\
&=6-\lp0,7u_n+1,8\rp\\
&=4,2-0,7u_n\\
&=0,7\lp6-u_n\right)
=0,7v_n\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/48.png)
ce qui montre que la suite est bien géométrique de raison
est bien géométrique de raison  et de premier terme
et de premier terme  .
.
- On en déduit alors que, pour tout entier
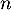 ,
,
![\[v_n=v_0\times q^n=4\times0,7^n\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/53.png)
puis, comme , que
, que
![\[u_n=6-4\tm0,7^n\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/55.png)
- On arrête les injections lorsque la quantité de médicament
présente dans le sang du patient est supérieure ou égale à 5,5 mg,
soit lorsque
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff&6-4\tm0,7^n\geqslant5,5\\
\iff&-4\tm0,7^n\geqslant-0,5\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/56.png)
soit, en divisant par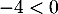 , puis en prenant le logarithme népérien qui est strictement croissant,
, puis en prenant le logarithme népérien qui est strictement croissant,
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff&0,7^n\leqslant\dfrac{-0,5}{-4}=0,125\\
\iff&\ln\lp0,7^n\rp=n\ln(0,7)\leqslant\ln(0,125)\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/58.png)
Enfin, en divisant par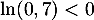 , on obtient finalement
, on obtient finalement
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff n\geqslant\dfrac{\ln(0,125)}{\ln(0,7)}\simeq5,8\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/60.png)
Comme on réalise une injection par heure, il faut donc en réaliser 6.
- Pour tout entier
Cacher la correction
Exercice 3: Bac 2021 - Suite récurrente
La suite 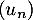 est définie sur
est définie sur 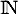 par
par 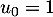 et pour tout entier naturel
et pour tout entier naturel  ,
,
![\[u_{n+1} = \dfrac34u_n + \dfrac14n + 1.\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021/5.png)
Cacher la correction
- Calculer, en détaillant les calculs,
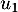 et
et 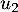 sous forme de fraction irréductible.
sous forme de fraction irréductible.
L'extrait, reproduit ci-contre, d'une feuille de calcul réalisée avec un tableur présente les valeurs des premiers termes de la suite 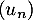 .
.
![\[\begin{tabular}{|c|*2{p{2.4cm}|}}\hline
& A&B \\ \hline
1 &$n$&$u_n$\\ \hline
2 &0 &1\\ \hline
3 &1 &1,75\\ \hline
4 &2 &2,5625\\ \hline
5 &3 &3,421875\\ \hline
6 &4 &4,31640625\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021/9.png)
-
- Quelle formule, étirée ensuite vers le bas, peut-on écrire dans la cellule B3 de la feuille de calcul pour obtenir les termes successifs de
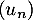 dans la colonne B ?
dans la colonne B ?
- Conjecturer le sens de variation de la suite
 .
.
- Quelle formule, étirée ensuite vers le bas, peut-on écrire dans la cellule B3 de la feuille de calcul pour obtenir les termes successifs de
-
- Démontrer par récurrence que, pour tout entier naturel
 , on a :
, on a :  .
.
- En déduire, en justifiant la réponse, le sens de variation et la limite de la suite
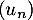 .
.
- Démontrer que :
![\[\lim_{n \to + \infty} \dfrac{u_n}n = 1\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021/15.png)
- Démontrer par récurrence que, pour tout entier naturel
- On désigne par
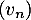 la suite définie sur
la suite définie sur  par
par 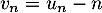
- Démontrer que la suite
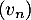 est géométrique
de raison
est géométrique
de raison  .
.
- En déduire que, pour tout entier naturel
 ,on a:
,on a:
 .
.
- Démontrer que la suite
Correction exercice 3
- Pour
 ,
, 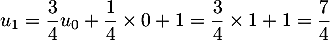 .
.
Pour ,
, 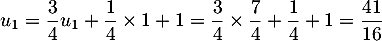 .
.
-
- La formule, étirée ensuite vers le bas, que l'on peut écrire dans la cellule B3 de la feuille de calcul pour obtenir les termes successifs de
 dans la colonne B est:
= 3/4 * B2 + 1/4 * A2 +1
dans la colonne B est:
= 3/4 * B2 + 1/4 * A2 +1
- La suite
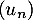 semble croissante.
semble croissante.
- La formule, étirée ensuite vers le bas, que l'on peut écrire dans la cellule B3 de la feuille de calcul pour obtenir les termes successifs de
-
- Soit
 la propriété:
la propriété:  .
.
Initialisation
Pour ,
, 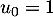 et
et 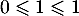 donc
donc 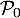 est vraie.
est vraie.
Hérédité
Supposons que, pour un certain entier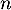 ,
, 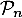 est vraie,
c'est-à-dire:
est vraie,
c'est-à-dire: 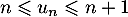 .
.
Alors,
![\[\begin{array}{ll}&n\leqslant u_n \leqslant n+1\\[.6em]
\iff&\dfrac34n\leqslant\dfrac34u_n\leqslant\dfrac34(n+1)\\[.8em]
\iff&\dfrac34n +\dfrac14n\leqslant\dfrac34u_n+\dfrac14n\leqslant\dfrac34(n+1)+\dfrac14n\\[.6em]
\iff&n \leqslant\dfrac34u_n+\dfrac14n \leqslant n+\dfrac34\\[7pt]
\iff&n+1 \leqslant\dfrac34u_n+\dfrac14n+1\leqslant n+\dfrac34+1\\
\iff&n+1 \leqslant u_{n+1}\leqslant n+\dfrac74\leqslant n+2\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/16.png)
ce qui montre que la propriété est encore vraie au rang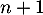 .
.
Conclusion On vient donc de démonter, d'après le principe de récurrence, que, pour tout entier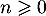 ,
,
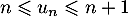 .
.
-
D'après la question précédente, pour tout
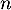 ,
, 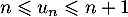 donc aussi, au rang suivant,
donc aussi, au rang suivant, 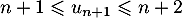 .
.
On a alors,
![\[n \leqslant u_n \leqslant n+1 \leqslant u_{n+1} \leqslant n+2\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/23.png)
et donc, entre autre que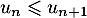 , c'est-à-dire que la suite
, c'est-à-dire que la suite 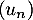 est croissante.
est croissante.
On a aussi de ces inégalités que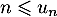 ,
et comme
,
et comme 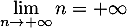 donc, par comparaison
(corollaire du théorème des gendarmes),
donc, par comparaison
(corollaire du théorème des gendarmes),
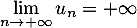 .
.
- Pour tout
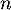 ,
, 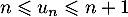 donc on a aussi
donc on a aussi
![\[1 \leqslant \dfrac{u_n}{n} \leqslant \dfrac{n+1}{n}=1+\dfrac{1}{n}\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/31.png)
avec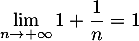 ,
donc, d'après le théorème des gendarmes:
,
donc, d'après le théorème des gendarmes: 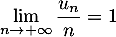 .
.
- Soit
- On désigne par
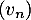 la suite définie sur
la suite définie sur  par
par 
- Pour tout
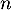 ,
, 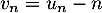
![\[\begin{array}{ll}v_{n+1}&=u_{n+1} - (n+1) \\[.4em]
&=\dfrac34u_n + \dfrac{1}{4}n+1 -n-1\\[.7em]
&=\dfrac34u_n -\dfrac34n\\[.7em]
&=\dfrac34\left( u_n -n\rp\\[.7em]
&=\dfrac{3}{4}v_n\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/39.png)
Donc la suite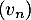 est géométrique de raison
est géométrique de raison 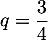 et de premier terme
et de premier terme 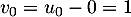
- On en déduit que, pour tout
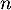 ,
,
![\[v_n=v_0\times q^n = \lp\dfrac34\rp^n\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/44.png)
et donc aussi que
![\[u_n=v_n+n=\lp\dfrac34\rp^n+n\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/45.png)
- Pour tout
Cacher la correction
Exercice 4: Bac septembre 2019 - Suite récurrente
Soit 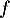 la fonction définie sur l'intervalle [0 ; 4] par
la fonction définie sur l'intervalle [0 ; 4] par
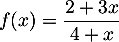 .
.
Partie A On considère la suite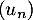 définie par :
définie par :
![\[u_0 = 3 \; \text{et pour tout entier naturel }\; n,\; u_{n+1} = f\left(u_n\right).\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR/4.png)
On admet que cette suite est bien définie.
Partie B On considère la suite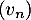 définie par :
définie par :
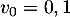 et pour tout entier naturel
et pour tout entier naturel  ,
, 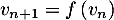 .
.
(0,0)(1.15,1.1)
\psline(1.1,1.1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1.15}{3 x mul 2 add x 4 add div}
\uput[d](0.8,0.8){$D$}\uput[u](0.8,0.92){\blue $\mathcal{C}_f$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR/32.png)
Partie A
Partie B
Annexe
(0,0)(1.15,1.1)
\psline(1.1,1.1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1.15}{3 x mul 2 add x 4 add div}
\uput[ul](1.1,1.1){$D$}\uput[d](1.1,1.03){\blue $\mathcal{C}_f$}
\psline[ArrowInside=->](0.1,0)(0.1,0.561)(0.561,0.561)(0.561,0.8074)(0.8074,0.8074)(0.8074,0.92)(0.92,0.92)
\psline(0.561,0)(0.561,0.561)
\psline(0.8074,0.8074)(0.8074,0)
\psline(0.92,0)(0.92,0.92)
\uput[d](0.1,-0.05){$v_0 =0,1$}\uput[d](0.561,-0.05){$v_1=0,561$}\uput[d](0.8074,-0.05){$v_2=0,807$}\uput[d](0.92,-0.05){$v_3=0,92$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR_c/59.png)
Cacher la correction
Partie A On considère la suite
On admet que cette suite est bien définie.
- Calculer
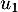 .
.
- Montrer que la fonction
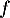 est croissante sur l'intervalle [0 ; 4].
est croissante sur l'intervalle [0 ; 4].
- Montrer que pour tout entier naturel
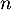 ,
,
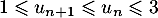 .
.
-
- Montrer que la suite
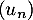 est convergente.
est convergente.
- On appelle
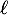 la limite de la suite
la limite de la suite 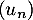 ; montrer l'égalité:
; montrer l'égalité:
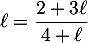 .
.
.
.
- Déterminer la valeur de la limite
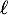 .
.
- Montrer que la suite
Partie B On considère la suite
- On donne en Annexe, à rendre avec la copie, la courbe représentative,
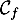 , de la
fonction
, de la
fonction 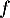 et la droite
et la droite 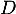 d'équation
d'équation 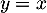 .
.
Placer sur l'axe des abscisses par construction géométrique les termes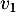 ,
, 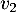 et
et 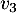 sur
l'annexe, à rendre avec la copie.
sur
l'annexe, à rendre avec la copie.
Quelle conjecture peut-on formuler sur le sens de variation et le comportement de la suite quand
quand  tend vers l'infini ?
tend vers l'infini ?
-
- Montrer que pour tout entier naturel
 ,
,
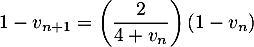 .
.
- Montrer par récurrence que pour tout entier naturel
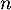 ,
,
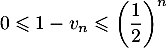 .
.
- Montrer que pour tout entier naturel
- La suite
 converge-t-elle ? Si oui, préciser sa limite.
converge-t-elle ? Si oui, préciser sa limite.
Annexe
(0,0)(1.15,1.1)
\psline(1.1,1.1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1.15}{3 x mul 2 add x 4 add div}
\uput[d](0.8,0.8){$D$}\uput[u](0.8,0.92){\blue $\mathcal{C}_f$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR/32.png)
Correction exercice 4
Partie A
-
 .
.
- La fonction
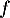 est définie et dérivable sur [0 ; 4] et sur cet intervalle :
est définie et dérivable sur [0 ; 4] et sur cet intervalle :
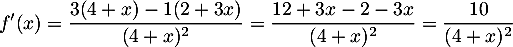
Quotient de nombres positifs ce nombre dérivé est positif quel que soit dans l'intervalle [0 ; 4]. La fonction
dans l'intervalle [0 ; 4]. La fonction 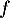 est donc croissante sur [0 ; 4].
est donc croissante sur [0 ; 4].
- Démonstration par récurrence :
Initialisation
On a d'après la première question :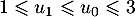 : l'encadrement est vrai au rang
: l'encadrement est vrai au rang  ;
;
Hérédité
Supposons que pour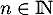 ,
, 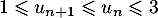 ; par croissance de la fonction
; par croissance de la fonction 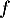 sur [0 ; 4], on
sur [0 ; 4], on
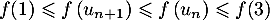 ou car
ou car 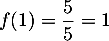 et
et 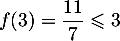 ,
,
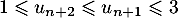 : la relation est donc vraie au rang
: la relation est donc vraie au rang  .
.
Conclusion : l'encadrement est vrai au rang et s'il est vrai à un rang quelconque
et s'il est vrai à un rang quelconque  il est vrai au rang suivant
il est vrai au rang suivant 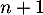 : d'après le principe de récurrence pour tout naturel
: d'après le principe de récurrence pour tout naturel  ,
,  .
.
-
- D'après la question précédente la suite
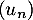 est décroissante, minorée par
est décroissante, minorée par 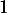 : elle converge donc vers une limite
: elle converge donc vers une limite  .
.
- De l'égalité
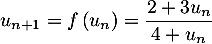 on en déduit par continuité de la fonction
on en déduit par continuité de la fonction 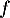 (puisque
(puisque 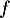 est dérivable) :
est dérivable) :
![\[\ell = \dfrac{2 + 3\ell}{4 + \ell}.\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR_c/27.png)
- On en déduit que
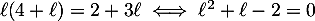 .
.
Or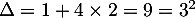 . Il y a deux solutions :
. Il y a deux solutions :
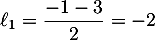 et
et 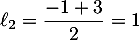 .
.
Comme![$\ell \in [1~;~3]$](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR_c/32.png) , la seule solution est
, la seule solution est  .
.
- D'après la question précédente la suite
Partie B
- Voir l'annexe.
On peut conjecturer que la suite est croissante et qu'elle a pour limite 1.
est croissante et qu'elle a pour limite 1.
-
-
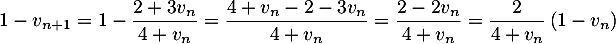 .
.
-
Initialisation pour
 ,
, 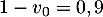 ; or
; or 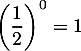 .
On a bien
.
On a bien 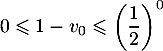 .
.
Hérédité Supposons qu'au rang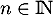 quelconque, on ait
quelconque, on ait 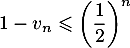 .
.
On a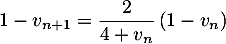 , donc d'après l'hypothèse de récurrence :
, donc d'après l'hypothèse de récurrence :
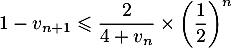 .
.
Or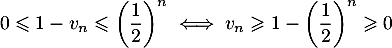 ; il suit que
; il suit que 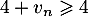 , donc en prenant les inverses
, donc en prenant les inverses 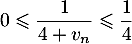 .
.
On a donc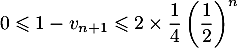 , soit finalement :
, soit finalement :
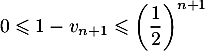 : l'encadrement est vrai au rang
: l'encadrement est vrai au rang 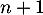 .
.
L'encadrement est vrai au rang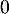 et s'il est vrai à un rang
et s'il est vrai à un rang 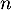 quelconque il est vrai au rang
quelconque il est vrai au rang 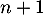 : d'après le principe de récurrence :
: d'après le principe de récurrence :
quel que soit le naturel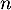 ,
, 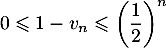 .
.
-
-
Comme
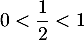 , on sait que
, on sait que  , donc l'encadrement trouvé à la question précédente montre que la la limite de
, donc l'encadrement trouvé à la question précédente montre que la la limite de 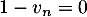 , donc :
, donc :
![\[\dsp\lim_{n \to + \infty} v_n = 1.\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR_c/58.png)
Annexe
(0,0)(1.15,1.1)
\psline(1.1,1.1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{1.15}{3 x mul 2 add x 4 add div}
\uput[ul](1.1,1.1){$D$}\uput[d](1.1,1.03){\blue $\mathcal{C}_f$}
\psline[ArrowInside=->](0.1,0)(0.1,0.561)(0.561,0.561)(0.561,0.8074)(0.8074,0.8074)(0.8074,0.92)(0.92,0.92)
\psline(0.561,0)(0.561,0.561)
\psline(0.8074,0.8074)(0.8074,0)
\psline(0.92,0)(0.92,0.92)
\uput[d](0.1,-0.05){$v_0 =0,1$}\uput[d](0.561,-0.05){$v_1=0,561$}\uput[d](0.8074,-0.05){$v_2=0,807$}\uput[d](0.92,-0.05){$v_3=0,92$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapSuites/ex13092019SR_c/59.png)
Cacher la correction
Exercice 5: Bac 2014, Nouvelle Calédonie - Suite récurrente, construction graphique des 1er termes, récurrence, somme des 1er termes et algorithme
On considère la fonction  définie sur l'intervalle
définie sur l'intervalle  par
par
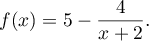
On admettra que est dérivable sur l'intervalle
est dérivable sur l'intervalle 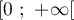 .
.
On a tracé en annexe 1 dans un repère orthonormé la courbe représentative de
représentative de 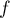 ainsi que la droite
ainsi que la droite 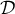 d'équation
d'équation 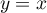 .
.
Annexe 1 à rendre avec la copie
![\psset{unit=1.35cm}
\begin{pspicture}(-0.5,-0.25)(8.1,7.2)
\psaxes[linewidth=1.25pt]{->}(0,0)(-0.5,-0.25)(8.1,7.2)
\psline[linecolor=cyan](7.2,7.2)
\psplot[plotpoints=4000,linewidth=1.25pt,linecolor=blue]{0}{8.1}{5 4 x 2 add div sub}
\uput[dl](0,0){O}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/ex114.NC/45.png)
Annexe 2 à rendre avec la copie

Nouvelle Calédonie, 2014
On considère la fonction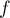 définie sur l'intervalle
définie sur l'intervalle 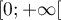 par
par
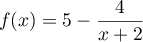 .
.
Annexe
![\psset{unit=1.35cm}
\begin{pspicture}(-0.5,-0.25)(8.1,7.2)
\psaxes[linewidth=1.25pt,arrowsize=2pt 3]{->}(0,0)(-0.5,-0.25)(8.1,7.2)
\psline[linecolor=cyan](7.2,7.2)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{8.1}{5 4 x 2 add div sub}
\uput[dl](0,0){O}
\psset{linecolor=red}
\psline(1,0)(1,3.67)
\psline(0,3.67)(3.67,3.67)
\psline(3.67,0)(3.67,4.294)
\psline(0,4.294)(4.294,4.294)
\psline(4.294,0)(4.294,4.364)
\uput*{8pt}[d](1,0){\red $M_0$}
\uput*{8pt}[d](3.67,0){\red $M_1$} \uput[l](0,3.67){\red $u_1$}
\uput*{8pt}[d](4.294,0){\red $M_2$} \uput[l](0,4.294){\red $u_2$}
\psline[linecolor=blue,linestyle=dashed](4.37,0)(4.37,4.37)
\uput[dr](4.37,0){\blue $\alpha$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/ex114.NC_c/81.png)
Annexe 2

Cacher la correction
On admettra que
On a tracé en annexe 1 dans un repère orthonormé la courbe
- Démontrer que
 est croissante sur l'intervalle
est croissante sur l'intervalle 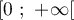 .
.
- Résoudre l'équation
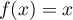 sur l'intervalle
sur l'intervalle  . On note
. On note 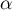 la solution.
la solution.
On donnera la valeur exacte de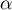 puis on en donnera une valeur approchée à
puis on en donnera une valeur approchée à 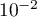 près.
près.
- On considère la suite
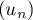 définie par
définie par 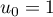 et, pour tout entier naturel
et, pour tout entier naturel 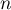 ,
, 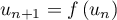 .
.
Sur la figure de annexe 1, en utilisant la courbe et la droite
et la droite  , placer les points
, placer les points  ,
, 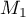 et
et 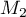 d'ordonnée nulle et d'abscisses respectives
d'ordonnée nulle et d'abscisses respectives 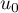 ,
, 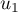 et
et 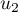 .
.
Quelles conjectures peut-on faire sur le sens de variation et la convergence de la suite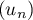 ?
?
-
- Démontrer, par récurrence, que, pour tout entier naturel
 ,
,
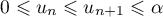
où est le réel défini dans la question 2.
est le réel défini dans la question 2.
- Peut-on affirmer que la suite
 est convergente ? On justifiera la réponse.
est convergente ? On justifiera la réponse.
- Démontrer, par récurrence, que, pour tout entier naturel
- Pour tout entier naturel
 , on définit la suite
, on définit la suite  par
par
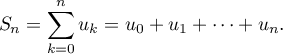
- Calculer
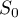 ,
, 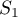 et
et 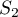 . Donner une valeur approchée des résultats à
. Donner une valeur approchée des résultats à 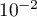 près.
près.
- Compléter l'algorithme donné en annexe 2 pour qu'il affiche la somme
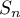 pour la valeur de l'entier
pour la valeur de l'entier 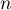 demandée à l'utilisateur.
demandée à l'utilisateur.
- Montrer que la suite
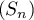 diverge vers
diverge vers 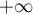 .
.
- Calculer
Annexe 1 à rendre avec la copie
![\psset{unit=1.35cm}
\begin{pspicture}(-0.5,-0.25)(8.1,7.2)
\psaxes[linewidth=1.25pt]{->}(0,0)(-0.5,-0.25)(8.1,7.2)
\psline[linecolor=cyan](7.2,7.2)
\psplot[plotpoints=4000,linewidth=1.25pt,linecolor=blue]{0}{8.1}{5 4 x 2 add div sub}
\uput[dl](0,0){O}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/ex114.NC/45.png)
Annexe 2 à rendre avec la copie

Correction exercice 5
Nouvelle Calédonie, 2014
On considère la fonction
-
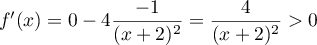 sur
sur 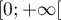 .
.
Donc la fonction est strictement croissante sur
est strictement croissante sur  .
.
- On résout dans
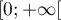 l'équation
l'équation 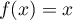 :
:
![$f(x) = x \iff 5-\dfrac{4}{x+2}=x \iff \dfrac{5(x+2)-4 -x(x+2)}{x+2} = 0 \iff
\dfrac{5x+10-4-x^2-2x}{x+2}=0\\[5pt]
\phantom{f(x)=x} \iff \dfrac{-x^2+3x+6}{x+2}=0 \iff
-x^2+3x+6 = 0 \text{ et }x+2 \neq 0](/Generateur-Devoirs/TS/ChapSuites/ex114.NC_c/10.png)
Le trinôme du second degré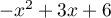 a pour discriminant
a pour discriminant 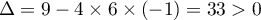 ,
et admet donc 2 solutions réelles:
,
et admet donc 2 solutions réelles: 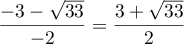 et
et 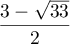 .
.
Cette deuxième solution est négative donc l'unique solution de l'équation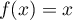 dans l'intervalle
dans l'intervalle 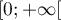 est
est 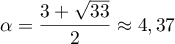 .
.
- On considère la suite
 définie par
définie par 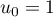 et, pour tout entier naturel
et, pour tout entier naturel  ,
, 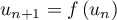 .
.
Sur la figure de annexe 1, on place les points ,
,  et
et  d'ordonnée nulle et d'abscisses respectives
d'ordonnée nulle et d'abscisses respectives 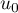 ,
, 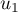 et
et 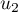 .
.
On peut conjecturer que la suite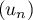 est croissante et converge vers
est croissante et converge vers 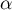 .
.
-
- On cherche à montrer que la propriété
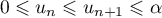 est vraie pour tout entier
est vraie pour tout entier  .
.
Initialisation: Pour ,
, 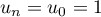 et
et 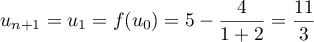 ; de plus
; de plus 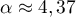 .
On a
.
On a 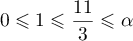 ce qui veut dire que la propriété est vraie au rang 0.
ce qui veut dire que la propriété est vraie au rang 0.
Hérédité: On suppose la propriété vraie au rang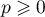 , autrement dit:
, autrement dit: 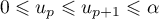 .
.
On sait d'après la question 1. que la fonction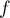 est strictement croissante sur
est strictement croissante sur 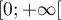 donc:
donc:
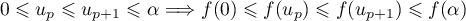
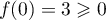 ,
, 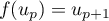 et
et 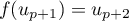 .
.
De plus, est solution de l'équation
est solution de l'équation 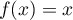 donc
donc 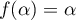 .
.
On a donc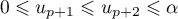 ; on peut dire que la propriété est vraie au rang
; on peut dire que la propriété est vraie au rang  .
.
Conclusion: On a donc démontré d'après le principe de récurrence, que, pour tout entier naturel ,
,  .
.
- Pour tout
 ,
, 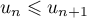 donc la suite
donc la suite 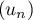 est croissante.
Pour tout
est croissante.
Pour tout 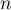 ,
,  donc la suite
donc la suite 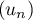 est majorée par
est majorée par  .
.
On en déduit que la suite est convergente.
est convergente.
- On cherche à montrer que la propriété
- Pour tout entier naturel
 , on définit la suite
, on définit la suite  par
par
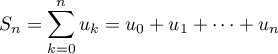 .
.
-
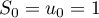 ;
;
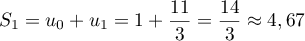
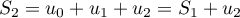 ;
; 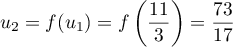 donc
donc
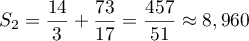 donc
donc 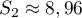 .
.
- On complète l'algorithme donné en annexe 2 pour qu'il affiche la somme
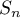 pour la valeur de l'entier
pour la valeur de l'entier 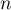 demandée à l'utilisateur.
demandée à l'utilisateur.
- On sait que la suite
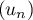 est croissante donc, pour tout
est croissante donc, pour tout  de
de  ,
,  .
.
Or , donc, pour tout
, donc, pour tout  ,
,  et donc
et donc
 .
Or
.
Or 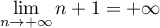 donc, d'après les théorèmes de comparaison sur les limites:
donc, d'après les théorèmes de comparaison sur les limites:
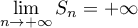
-
Annexe
![\psset{unit=1.35cm}
\begin{pspicture}(-0.5,-0.25)(8.1,7.2)
\psaxes[linewidth=1.25pt,arrowsize=2pt 3]{->}(0,0)(-0.5,-0.25)(8.1,7.2)
\psline[linecolor=cyan](7.2,7.2)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{8.1}{5 4 x 2 add div sub}
\uput[dl](0,0){O}
\psset{linecolor=red}
\psline(1,0)(1,3.67)
\psline(0,3.67)(3.67,3.67)
\psline(3.67,0)(3.67,4.294)
\psline(0,4.294)(4.294,4.294)
\psline(4.294,0)(4.294,4.364)
\uput*{8pt}[d](1,0){\red $M_0$}
\uput*{8pt}[d](3.67,0){\red $M_1$} \uput[l](0,3.67){\red $u_1$}
\uput*{8pt}[d](4.294,0){\red $M_2$} \uput[l](0,4.294){\red $u_2$}
\psline[linecolor=blue,linestyle=dashed](4.37,0)(4.37,4.37)
\uput[dr](4.37,0){\blue $\alpha$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/ex114.NC_c/81.png)
Annexe 2

Cacher la correction
Exercice 6: Bac 2013, France métroplitaine - Suite récurrente, récurrence, somme de termes
Bac S, 20 juin 2013, 5 points
Soit la suite numérique définie sur
définie sur  par :
par :

Cacher la correction
Soit la suite numérique
-
- Calculer
 et
et  . On pourra en donner
des valeurs approchées à
. On pourra en donner
des valeurs approchées à  près.
près.
- Formuler une conjecture sur le sens de variation de cette suite.
- Calculer
-
- Démontrer que pour tout entier naturel
 ,
,

- Démontrer que pour tout entier naturel
 ,
,

- En déduire une validation de la conjecture précédente.
- Démontrer que pour tout entier naturel
- On désigne par
 la suite
définie sur
la suite
définie sur  par
par  .
.
- Démontrer que la suite
 est une suite
géométrique de raison
est une suite
géométrique de raison  .
.
- En déduire que pour tout entier naturel
 ,
,

- Déterminer la limite de la suite
 .
.
- Démontrer que la suite
- Pour tout entier naturel non nul
 , on pose:
, on pose:

- Exprimer
 en fonction de
en fonction de  .
.
- Déterminer la limite de la suite
 .
.
- Exprimer
Correction exercice 6
-
- On calcule les premiers termes, par exemple en utilisant le
mode récurrence de la calculatrice, et on obtient:
 ;
;
 ;
;
 ;
;

- On peut donc émettre la conjecture que la suite est croissante. On pourra en tout cas affirmer qu'elle n'est pas décroissante.
- On calcule les premiers termes, par exemple en utilisant le
mode récurrence de la calculatrice, et on obtient:
-
- Nous allons montrer par récurrence,
pour tout entier naturel
 , la propriété
, la propriété  :
:  .
Initialisation : Puisque l'on a
.
Initialisation : Puisque l'on a  et
et  , on vérifie bien :
, on vérifie bien :
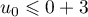 : la propriété
: la propriété  est bien vraie.
est bien vraie.
Hérédité : Pour un entier naturel donné, on suppose la
propriété
naturel donné, on suppose la
propriété  vraie.
On a
vraie.
On a  .
Par hypothèse de récurrence :
.
Par hypothèse de récurrence :  En multipliant par un nombre positif:
En multipliant par un nombre positif:
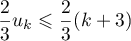 ,
soit
,
soit  Puis, en ajoutant un même nombre dans chaque membre :
Puis, en ajoutant un même nombre dans chaque membre :
 Ce qui donne :
Ce qui donne :  .
On a donc
.
On a donc  ,
c'est à dire que la propriété
,
c'est à dire que la propriété  est encore vraie.
Conclusion: Puisque la propriété
est encore vraie.
Conclusion: Puisque la propriété  est vraie
et que nous avons prouvé l'hérédité, on peut en déduire que pour
tout entier naturel
est vraie
et que nous avons prouvé l'hérédité, on peut en déduire que pour
tout entier naturel  , on a
, on a  vraie, c'est à dire
que pour tout entier naturel
vraie, c'est à dire
que pour tout entier naturel  , on a bien
, on a bien  .
.
-
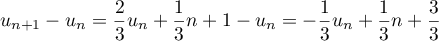 On a donc bien
On a donc bien  .
Comme on l'a montré à la question précédente, pour tout
.
Comme on l'a montré à la question précédente, pour tout  naturel, on a
naturel, on a  ce qui équivaut à dire que la
différence
ce qui équivaut à dire que la
différence  est positive, et elle le reste en étant
multipliée par
est positive, et elle le reste en étant
multipliée par  , donc la différence entre deux termes
consécutifs étant positive, on confirme bien que notre conjecture
était correcte : la suite
, donc la différence entre deux termes
consécutifs étant positive, on confirme bien que notre conjecture
était correcte : la suite  est bien croissante,
dès le rang 0.
est bien croissante,
dès le rang 0.
- Nous allons montrer par récurrence,
pour tout entier naturel
-
- Exprimons, pour un entier
 naturel quelconque,
naturel quelconque,  en fonction de
en fonction de  :
:
 Donc
Donc  .
La relation de récurrence obtenue confirme que la suite
.
La relation de récurrence obtenue confirme que la suite  est bien géométrique de raison
est bien géométrique de raison  et de
premier terme
et de
premier terme  .
.
- On peut donc en déduire que pour totu entier
 ,
,
 .
Enfin, puisque l'on a, pour tout
.
Enfin, puisque l'on a, pour tout  ,
,  , on en déduit :
, on en déduit :
 , et donc on aboutit bien à l'expression demandée :
, et donc on aboutit bien à l'expression demandée :
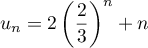 .
.
- Puisque la raison
 est strictement comprise entre
est strictement comprise entre  et
et
 , on en déduit que la limite de la suite
, on en déduit que la limite de la suite  est 0, et donc par
limite d'une somme de suites, la limite de la suite
est 0, et donc par
limite d'une somme de suites, la limite de la suite  est donc
est donc
 , et la suite
, et la suite  est donc divergente.
est donc divergente.
- Exprimons, pour un entier
-
-
 est la somme de
est la somme de  premiers termes de la suite
premiers termes de la suite  .
.
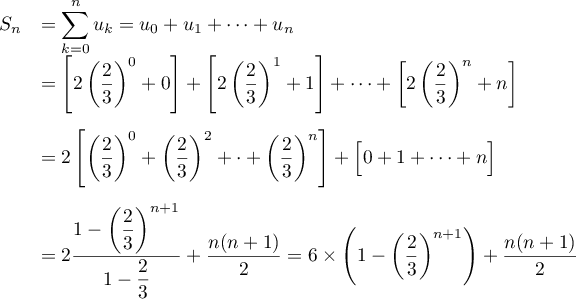
- On en déduit:
 .
Puisque
.
Puisque  on a :
on a :
 ,
et donc:
,
et donc:
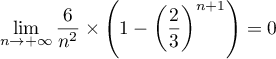 .
De plus
.
De plus  ,
et donc finalement, par limite d'une somme,
,
et donc finalement, par limite d'une somme,
 .
.
-
Cacher la correction
Exercice 7: Bac 2013, Liban - Suite récurrente, algorithme
(Bac S, 28 mai 2013, Liban, 4 points)
On considère la suite numérique définie pour tout
entier naturel
définie pour tout
entier naturel  par
par

Partie A
Partie B Recherche de la limite de la suite
On considère la suite définie pour tout
définie pour tout  entier
naturel par
entier
naturel par

Partie A
Partie B
Cacher la correction
On considère la suite numérique

Partie A
- On souhaite écrire un algorithme affichant, pour un entier naturel
 donné, tous les termes de la suite, du rang
donné, tous les termes de la suite, du rang  au rang
au rang  .
Parmi les trois algorithmes suivants, un seul convient. Préciser lequel en justifiant la réponse.
.
Parmi les trois algorithmes suivants, un seul convient. Préciser lequel en justifiant la réponse.

- Pour
 on obtient l'affichage suivant :
on obtient l'affichage suivant :

Pour , les derniers termes affichés sont :
, les derniers termes affichés sont :

Quelles conjectures peut-on émettre concernant la suite ?
?
-
- Démontrer par récurrence que, pour tout entier naturel
 ,
,
 .
.
- Démontrer que, pour tout entier naturel
 ,
,
 .
La suite
.
La suite  est-elle monotone ?
est-elle monotone ?
- Démontrer que la suite
 est convergente.
est convergente.
- Démontrer par récurrence que, pour tout entier naturel
Partie B Recherche de la limite de la suite
On considère la suite
- Démontrer que
 est une suite arithmétique de
raison
est une suite arithmétique de
raison 
- En déduire l'expression de
 , puis celle de
, puis celle de
 en fonction de
en fonction de  .
.
- Déterminer la limite de la suite
 .
.
Correction exercice 7
Partie A
- L'algorithme n
 1 calcule bien tous les termes de
1 calcule bien tous les termes de  à
à
 mais n'affiche par contre que le dernier
mais n'affiche par contre que le dernier  .
.
Dans l'algorithme n 2, à chaque boucle la valeur de
2, à chaque boucle la valeur de  est
remise à
est
remise à  . cet algorithme
calcule donc
. cet algorithme
calcule donc  fois de suite
fois de suite  à partir de
à partir de
 et ne calcule antre autre pas les termes de
et ne calcule antre autre pas les termes de  à
à  .
.
L'algorithme n 3 calcule tous les termes de
3 calcule tous les termes de  à
à  et
les affiche bien successivement (l'affichage se fait dans la boucle,
après chaque calcul de
et
les affiche bien successivement (l'affichage se fait dans la boucle,
après chaque calcul de  ).
).
L'algorithme n 3 est donc l'algorithme qui convient.
3 est donc l'algorithme qui convient.
- D'après les tables de valeurs de la suite
la suite
 semble croissante et converger vers
un nombre proche de
semble croissante et converger vers
un nombre proche de  .
.
-
- Montrons par récurrence
que, pour tout entier
 ,
,
 .
.
Initialisation: Pour , on a bien
, on a bien  car
car  ;
ainsi la propriété est vraie au rang
;
ainsi la propriété est vraie au rang  .
.
Hérédité: Supposons que pour un certain entier ,
on ait
,
on ait  .
.
On a alors ,
puis
,
puis
 ,
car la fonction inverse est décroissante sur
,
car la fonction inverse est décroissante sur  .
.
Ainsi, en multipliant par ,
,
 .
.
On a donc alors ,
et la propriété est donc encore vraie au rang
,
et la propriété est donc encore vraie au rang  .
.
Conclusion: D'après le principe de récurrence, la propriété est vraie pour tout entier naturel
est vraie pour tout entier naturel
 .
.
- Pour tout entier
 ,
,
 .
.
Or, d'après la question précédente, pour tout ,
,  ,
ainsi
,
ainsi  donc
donc  (en particulier
(en particulier  ),
et
),
et  ,
d'où
,
d'où
 .
.
Ainsi la suite est strictement croissante.
est strictement croissante.
- Comme la suite est croissante et majorée par 3, elle
converge donc vers une limite
 inférieure ou égale à 3.
inférieure ou égale à 3.
- Montrons par récurrence
que, pour tout entier
Partie B
-

ainsi la suite est arithmétique de raison
est arithmétique de raison
 .
.
- On en déduit que, pour tout entier
 ,
,
 ,
avec
,
avec  ,
et donc,
,
et donc,
 .
.
De plus ,
et on a donc,
,
et on a donc,
 .
.
- Comme
 ,
on a donc
,
on a donc  .
.
Cacher la correction
Exercice 8: Bac 2013, Amérique du nord - suite récurrente, algorithme, suite logarithmique intermédiaire géométrique
On considère la suite 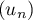 définie par
définie par 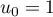 et, pour tout entier naturel
et, pour tout entier naturel 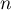 ,
,
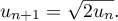
Amérique du Nord, 2013
On considère la suite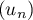 définie par
définie par 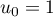 et, pour tout entier naturel
et, pour tout entier naturel  ,
,
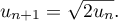
Cacher la correction
- On considère l'algorithme suivant:

- Donner une valeur approchée à
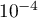 près du résultat qu'affiche cet algorithme lorsque l'on choisit
près du résultat qu'affiche cet algorithme lorsque l'on choisit 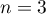 .
.
- Que permet de calculer cet algorithme ?
- Le tableau ci-dessous donne des valeurs approchées obtenues à l'aide de cet algorithme pour certaines valeurs de
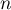 .
.
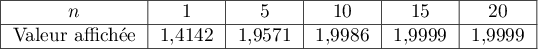
Quelles conjectures peut-on émettre concernant la suite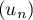 ?
?
- Donner une valeur approchée à
-
- Démontrer que, pour tout entier naturel
 .
.
- Déterminer le sens de variation de la suite
 .
.
- Démontrer que la suite
 est convergente. On ne demande pas la valeur de sa limite.
est convergente. On ne demande pas la valeur de sa limite.
- Démontrer que, pour tout entier naturel
- On considère la suite
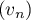 définie, pour tout entier naturel
définie, pour tout entier naturel  , par
, par 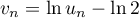 .
.
- Démontrer que la suite
 est la suite géométrique de raison
est la suite géométrique de raison  et de premier terme
et de premier terme
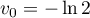 .
.
- Déterminer, pour tout entier naturel
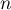 , l'expression de
, l'expression de 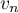 en fonction de
en fonction de 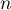 , puis de
, puis de 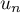 en fonction de
en fonction de  .
.
- Déterminer la limite de la suite
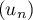 .
.
- Recopier l'algorithme ci-dessous et le compléter par les instructions du traitement et de la sortie, de façon à afficher en sortie la plus petite valeur de
 telle que
telle que 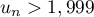 .
.

- Démontrer que la suite
Correction exercice 8
Amérique du Nord, 2013
On considère la suite
-
- Pour
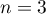 , la variable
, la variable  de la boucle varie de 1 à 3:
de la boucle varie de 1 à 3:
- Pour
 , on affecte à
, on affecte à 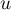 la valeur
la valeur 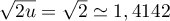
- Pour
 , on affecte à
, on affecte à 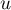 la valeur
la valeur 
- Pour
 , on affecte à
, on affecte à  la valeur
la valeur 
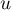 trouvée:
trouvée: 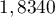 .
.
- Pour
- Cet algorithme permet de calculer et d'afficher le terme de rang
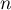 de la suite
de la suite 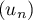 .
.
- D'après ce tableau des valeurs approchées, on peut conjecturer que la suite est croissante et converge vers 2.
- Pour
-
- Démontrons par récurrence que, pour tout entier naturel
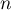 ,
, 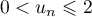 .
Initialisation: Pour
.
Initialisation: Pour  ,
, 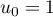 , donc on a bien
, donc on a bien 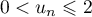 .
Hérédité: Supposons que pour un entier naturel
.
Hérédité: Supposons que pour un entier naturel 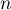 on ait
on ait  , alors,
, alors,
en multiplinat ces inégalités par ,
,  ,
,
puis, comme la fonction racine carrée est strictement croissante sur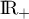 , on a
, on a 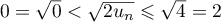 .
.
Ainsi, comme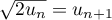 , on a donc bien encore, au rang
, on a donc bien encore, au rang
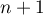 ,
, 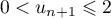 .
.
Conclusion: On vient donc de démontrer, d'après le principe de récurrence, que pour tout entier naturel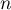 ,
,
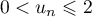 .
.
- Pour déterminer le sens de variation de la suite, on peut
procéder de (au moins) deux façons:
1ère méthode: par récurrence.
Initialisation: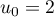 et
et 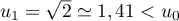 .
On a donc initialement, pour
.
On a donc initialement, pour 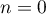 ,
, 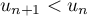 .
.
Hérédité: Supposons que pour un entier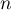 , on ait
, on ait 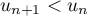 , alors,
, alors,
en multipliant par ,
, 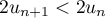 ,
,
puis, comme la fonction racine carrée est strictement croissante sur et que, d'après la question précédente,
et que, d'après la question précédente, 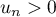 pour
tout
pour
tout 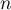 , on a donc
, on a donc
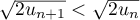 ,
,
soit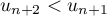 , et la propriété
, et la propriété 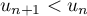 est encore
vraie au rang
est encore
vraie au rang  suivant.
suivant.
Conclusion: On vient donc de démontrer, d'après le principe de récurrence, que pour tout entier ,
, 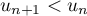 ,
c'est-à-dire que la suite
,
c'est-à-dire que la suite 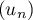 est strictement
croissante.
est strictement
croissante.
2ème méthode: démonstration directe.
Pour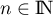 , on a
, on a
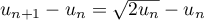 ,
soit, en utilisant la quantité conjuguée:
,
soit, en utilisant la quantité conjuguée:
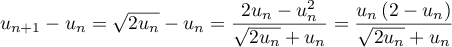
Or, d'après la question précédente,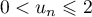 , et donc,
, et donc, 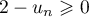 ,
et
,
et 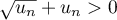 .
.
On a donc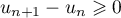 , et la suite
, et la suite 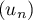 est
donc croissante.
est
donc croissante.
- On vient de prouver la suite
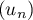 est strictement
croissante et est majorée par 2, on en déduit qu'elle converge
vers une limite réelle
est strictement
croissante et est majorée par 2, on en déduit qu'elle converge
vers une limite réelle  .
.
- Démontrons par récurrence que, pour tout entier naturel
-
- Pour tout entier naturel
 ,
, 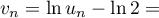 ,
donc,
,
donc,
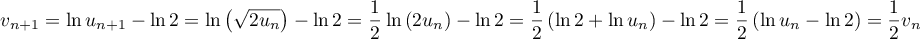
Ainsi,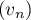 est la suite géométrique de raison
est la suite géométrique de raison  et de 1er terme
et de 1er terme 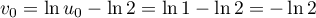 .
.
- On déduit de ce qui précède que pour tout entier naturel
 ,
,
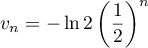 ,
puis que
,
puis que  .
.
- Comme
 ,
,
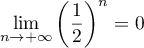 et donc
et donc 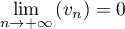 .
.
Comme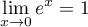 , par composition des limites on obtient:
, par composition des limites on obtient:
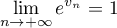 et finalement:
et finalement: 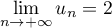 .
.
-

- Pour tout entier naturel
Cacher la correction
Exercice 9: Bac 2013, Asie - Un exercice bien complet sur les suites, et avec un algorithme
Partie A
On considère la suite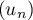 définie par:
définie par: 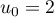 et, pour tout entier naturel
et, pour tout entier naturel  :
:
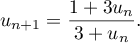
On admet que tous les termes de cette suite sont définis et strictement positifs.
Partie B
On considère la suite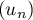 définie par:
définie par: 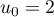 et, pour tout entier naturel
et, pour tout entier naturel 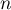 :
:
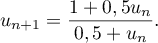
On admet que tous les termes de cette suite sont définis et strictement positifs.
Partie A
Partie B
Cacher la correction
On considère la suite
On admet que tous les termes de cette suite sont définis et strictement positifs.
- Démontrer par récurrence que, pour tout entier naturel
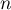 , on a :
, on a : 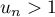 .
.
-
- Établir que, pour tout entier naturel
 , on a:
, on a: 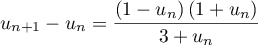 .
.
- Déterminer le sens de variation de la suite
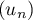 .
.
En déduire que la suite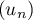 converge.
converge.
- Établir que, pour tout entier naturel
Partie B
On considère la suite
On admet que tous les termes de cette suite sont définis et strictement positifs.
- On considère l'algorithme suivant :

Reproduire et compléter le tableau suivant, en faisant fonctionner cet algorithme pour . Les valeurs de
. Les valeurs de  seront arrondies au millième.
seront arrondies au millième.
![\begin{tabular}{|*4{p{1.5cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&1&2& 3\\ \hline
\rule[1.4cm]{0.3cm}{-0.8cm}
$u$&&&\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie/18.png)
- Pour
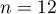 , on a prolongé le tableau précédent et on a obtenu :
, on a prolongé le tableau précédent et on a obtenu :
![\begin{tabular}{|c|*{9}{p{1.3cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&4&5&6&7&8&9&10&11&12\\ \hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$u$&\footnotesize{1,0083}&\footnotesize{0,9973}&\footnotesize{1,0009}&\footnotesize{0,9997}&\footnotesize{1,0001}&\footnotesize{0,99997}&\footnotesize{1,00001}&\footnotesize{0,999996}&\footnotesize{1,000001}\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie/20.png)
Conjecturer le comportement de la suite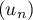 à l'infini.
à l'infini.
- On considère la suite
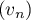 définie, pour tout entier naturel
définie, pour tout entier naturel 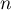 , par :
, par :  .
.
- Démontrer que la suite
 est géométrique de raison
est géométrique de raison  .
.
- Calculer
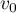 puis écrire
puis écrire 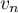 en fonction de
en fonction de 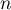 .
.
- Démontrer que la suite
-
- Montrer que, pour tout entier naturel
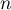 , on a:
, on a: 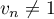 .
.
- montrer que, pour tout entier naturel
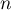 , on a:
, on a: 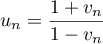 .
.
- Déterminer la limite de la suite
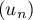 .
.
- Montrer que, pour tout entier naturel
Correction exercice 9
Partie A
- Initialisation : la relation est vraie au rang
 ;
;
Hérédité : supposons qu'il existe un naturel tel que
tel que  .
.
 .
.
Par hypothèse de récurrence on a:
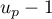 et comme
et comme 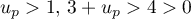 donc son inverse
donc son inverse 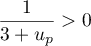 et finalement
et finalement 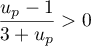 , c'est-à-dire que
, c'est-à-dire que 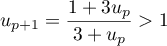
Conclusion: on a démontré, d'après le principe de récurrence, que pour tout entier naturel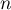 ,
, 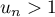 .
.
-
- Pour tout entier naturel
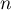 ,
, 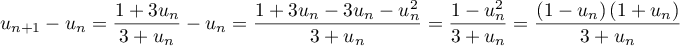 .
.
- On sait que pour tout entier
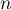 ,
, 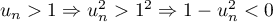 et comme
et comme 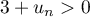 , on a
finalement
, on a
finalement 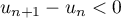 , ce qui signifie que la suite
, ce qui signifie que la suite 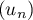 est décroissante.
est décroissante.
La suite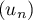 est décroissante et minorée par
est décroissante et minorée par  : elle converge donc vers une limite supérieure ou égale à
: elle converge donc vers une limite supérieure ou égale à 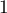 .
.
- Pour tout entier naturel
Partie B
-
![\begin{tabular}{|*{4}{p{1.5cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&1&2& 3\\ \hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$u$&0,800&1,077&0,976\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie_c/22.png)
- La suite semble converger vers
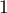 .
.
-
-
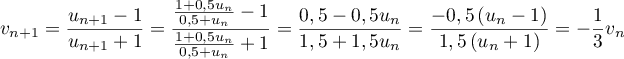 .
.
La suite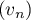 est donc géométrique de raison
est donc géométrique de raison 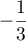 .
.
- On a
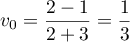 .
.
On sait qu'alors pour tout naturel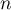 ,
, 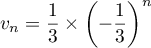 .
.
-
-
- Quel que soit le naturel
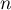 ,
, 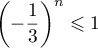 ,
donc
,
donc 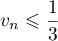 et par conséquent
et par conséquent 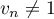 .
.
-
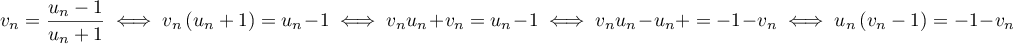 et comme
et comme 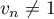 ,
,
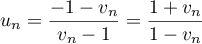 .
.
- Comme
 , on sait que
, on sait que 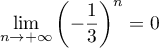 , soit
, soit 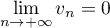 , donc d'après le résultat précédent
, donc d'après le résultat précédent 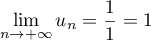 .
.
- Quel que soit le naturel
Cacher la correction
Exercice 10: Bac 2010, Centres étrangers - Suite et fonction
Centres étrangers, juin 2010
Soit la fonction définie sur l'intervalle
la fonction définie sur l'intervalle  par
par
 .
.
Le but de cet exercice est d'étudier des suites définies par
un premier terme positif ou nul
définies par
un premier terme positif ou nul  et vérifiant pour tout entier
naturel
et vérifiant pour tout entier
naturel  ,
,  .
.
Centres étrangers, juin 2010. est la fonction définie sur
est la fonction définie sur  par
par
 .
.
Cacher la correction
Soit
 la fonction définie sur l'intervalle
la fonction définie sur l'intervalle  par
par
 .
.
Le but de cet exercice est d'étudier des suites
 définies par
un premier terme positif ou nul
définies par
un premier terme positif ou nul  et vérifiant pour tout entier
naturel
et vérifiant pour tout entier
naturel  ,
,  .
.
- Etude de propriétés de la fonction

- Etudier le sens de variation de la fonction
 sur
sur  .
.
- Résoudre dans l'intervalle
 l'équation
l'équation
 .
On note
.
On note  la solution.
la solution.
- Montrer que si
 appartient à l'intervalle
appartient à l'intervalle  ,
alors
,
alors  appartient à l'intervalle
appartient à l'intervalle  .
.
- Etudier le sens de variation de la fonction
- Etude de la suite
 pour
pour 
Dans cette question, on considère la suite définie par
définie par
 et pour tout entier naturel
et pour tout entier naturel  ,
,
 .
.
- Représenter graphiquement la courbe représentative de la
fonction
 , et placer le points
, et placer le points  de coordonnées
de coordonnées  et construire les points
et construire les points  ,
,  ,
,  et
et  d'ordonnée
nulle et d'abscisses respectives
d'ordonnée
nulle et d'abscisses respectives  ,
,  ,
,  et
et  .
.
Quelles conjectures peut-on émettre quant au sens de variation et à la convergence de la suite ?
?
- Démontrer par récurrence que, pour tout entier naturel
 :
:
 .
.
Quel est alors le sens de variation de la suite ?
?
- Représenter graphiquement la courbe représentative de la
fonction
Correction exercice 10
Centres étrangers, juin 2010.
 est la fonction définie sur
est la fonction définie sur  par
par
 .
.
- Etude de propriétés de la fonction

- Pour tout
 ,
,
 .
.

-
 , en multipliant par
, en multipliant par  (car
(car  )
et donc,
)
et donc,
 .
.
Cette équation du second degré a pour discriminant , et admet donc deux solutions réelles distinctes:
, et admet donc deux solutions réelles distinctes:
 et
et
 .
.
Comme , l'équation
, l'équation  admet donc sur
admet donc sur  une seule solution
une seule solution  .
.
- Comme
 est strictement croissante sur
est strictement croissante sur  ,
on a
,
on a
 .
.
Or, et
et  .
Ainsi,
.
Ainsi,
 .
.
Ainsi, si , alors
, alors  .
.
- Pour tout
- Etude de la suite
 pour
pour 
Dans cette question, on considère la suite définie par
définie par
 et pour tout entier naturel
et pour tout entier naturel  ,
,
 .
.
-

On peut conjecturer que la suite est croissante, et
qu'elle converge vers
est croissante, et
qu'elle converge vers  .
.
-
Initialisation:
Pour
 , on a
, on a  , et
, et  ,
et ainsi on a donc bien
,
et ainsi on a donc bien
 .
.
Hérédité: Supposons que pour un entier on ait
on ait
 .
.
Alors, comme la fonction est croissante sur
est croissante sur  ,
,
 .
.
Or, ,
,
 ,
,
 ,
et
,
et  .
.
On a donc ainsi, ,
ce qui montre que la propriété est encore vraie au rang
,
ce qui montre que la propriété est encore vraie au rang  .
.
Conclusion: On vient donc de démontrer, d'après le principe de récurrence, que pour tout entier naturel ,
,
 .
.
On déduit en particulier de la propriété précédente que la suite est croissante (et bornée par
est croissante (et bornée par  et
et  ).
).
-
Cacher la correction
Exercice 11: Bac 2010, Antilles-Guyane - Suite récurrente, somme des 1er termes
Antilles-Guyane, septembre 2010
On considère la suite de nombres réels définie sur
définie sur  par:
par:

Antilles-Guyane, septembre 2010
Cacher la correction
On considère la suite de nombres réels
 définie sur
définie sur  par:
par:

- Calculer
 et en déduire que la suite
et en déduire que la suite  n'est ni
arithmétique, ni géométrique.
n'est ni
arithmétique, ni géométrique.
- On définit la suite
 en posant, pour tout entier naturel
en posant, pour tout entier naturel  ,
,
 .
.
- Calculer
 .
.
- Exprimer
 en fonction de
en fonction de  .
.
- En déduire que la suite
 est géométrique de raison
est géométrique de raison
 .
.
- Exprimer
 en fonction de
en fonction de  .
.
- Calculer
- On définit la suite
 en posant, pour tout entier naturel
en posant, pour tout entier naturel  ,
,
 .
.
- Cacluler
 .
.
- En utilisant l'égalité
 ,
exprimer
,
exprimer  en fonction de
en fonction de  et de
et de  .
.
- En déduire que pour tout
 de
de  ,
,
 .
.
- Exprimer
 en fonction de
en fonction de  .
.
- Cacluler
- Montrer que pour tout entier naturel
 :
:
 .
.
- Pour tout entier naturel
 ,
on pose
,
on pose
 .
Démontrer par récurrence que pour tout
.
Démontrer par récurrence que pour tout  de
de  :
:
 .
.
Correction exercice 11
Antilles-Guyane, septembre 2010
-
 .
.
On a donc, et
et  ce qui montre
que
ce qui montre
que  n'est pas arithmétique.
n'est pas arithmétique.
De même, et
et  ce qui montre que
ce qui montre que  n'est pas
non plus géométrique.
n'est pas
non plus géométrique.
-
-
 .
.
-
 .
.
- La suite
 est donc géométrique de raison
est donc géométrique de raison
 .
.
- On a alors, pour tout entier naturel
 ,
,
 .
.
-
-
-
 .
.
-
 d'après 2.
d'après 2.
- On a ainsi,

-
 est donc une suite arithmétique de raison 2 et de
premier terme
est donc une suite arithmétique de raison 2 et de
premier terme  ,
et on a donc, pour tout entier naturel
,
et on a donc, pour tout entier naturel  ,
,
 .
.
-
- On a
 .
.
- Initialisation:
Pour
 , on a
, on a  ,
donc la propriété est vraie.
,
donc la propriété est vraie.
Hérédité: Supposons que pour un entier naturel , on ait
, on ait
 .
.
Alors, , d'après l'hypothèse de récurrence.
, d'après l'hypothèse de récurrence.
Ainsi, ,
ce qui montre que la formule est alors encore vraie au rang
,
ce qui montre que la formule est alors encore vraie au rang  .
.
Conclusion: On vient donc de montrer, d'après le principe de récurrence, que pour tout entier naturel ,
,
 .
.
Cacher la correction
Exercice 12: Bac 2009, France métropolitaine - Suite récurrente
(Baccalauréat France métropolitaine, juin 2009, 4 points)
Les deux questions de cet exercice sont indépendantes.
Cacher la correction
- On considère la suite
 définie par
définie par  et, pour
tout entier naturel
et, pour
tout entier naturel  :
:

On pose, pour tout entier naturel ,
,  .
.
- Pour tout nombre entier naturel
 , calculer
, calculer  en
fonction de
en
fonction de  .
.
Quelle est la nature de la suite ?
?
- Démontrer que pour tout entier naturel
 :
:

- Etudier la convergence de la suite
 .
.
- Pour tout nombre entier naturel
- On considère la suite
 dont les termes vérifient,
pour tout nombre entier
dont les termes vérifient,
pour tout nombre entier  :
:
Le tableau suivant donne les premiers termes de cette suite:

- Détailler le calcul permettant d'obtenir
 .
.
- Dans cette question toute trace de recherche, même
incomplète, ou d'initiative, même non fructueuse, sera prise en
compte dans l'évaluation.
Donner la nature de la suite
 . Calculer
. Calculer  .
.
- Détailler le calcul permettant d'obtenir
Correction exercice 12
-
- Pour tout nombre entier naturel
 ,
,
 .
.
On en déduit que est géométrique de raison
est géométrique de raison
 et de premier terme
et de premier terme
 .
.
- D'après la question précédente,
pour tout entier
 ,
,
 ,
et donc que,
pour tout entier n ,
,
et donc que,
pour tout entier n ,
 .
.
- Comme
 ,
,
 ,
et donc,
,
et donc,  .
.
- Pour tout nombre entier naturel
-
- Pour
 ,
,
 , d'où,
, d'où,
 .
.
- D'après les valeurs de
 pour les premiers entiers,
on peut conjecturer que
pour les premiers entiers,
on peut conjecturer que  .
.
Démonstration de la conjecture: Démonstration par récurrence.
Initialisation: La relation est vraie pour tous les entiers .
.
Hérédité: Supposons que pour un certain entier ,
,
 (hypothèse de récurrence), alors,
(hypothèse de récurrence), alors,
 d'après l'hypothèse de
récurrence.
d'après l'hypothèse de
récurrence.
On a donc, , soit donc
, soit donc
 .
.
Ainsi, l'expression est encore vraie au rang .
.
On a ainsi démontré d'après le principe de récurrence que, pour tout entier ,
,  .
On en déduit que
.
On en déduit que .
.
- Pour
Cacher la correction
Exercice 13: Bac 2008, La Réunion - Suite récurrente, somme des termes d'une suite arithmétique, récurrence
On considère la suite 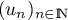 définie par:
définie par:
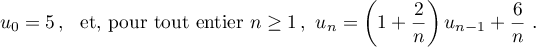
(Baccalauréat La Réunion, juin 2008, 5 points)
Cacher la correction
-
- Calculer
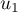 .
.
- Les valeurs de
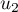 ,
, 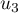 ,
, 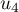 ,
, 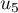 ,
, 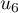 ,
, 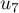 ,
,
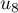 ,
, 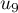 ,
, 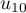 ,
, 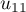 sont respectivement égales à:
sont respectivement égales à:
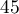 ,
, 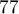 ,
, 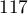 ,
, 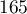 ,
, 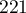 ,
, 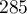 ,
, 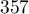 ,
, 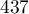 ,
, 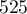 ,
,
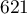 .
.
A partir de ces données, conjecturer la nature de la suite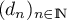 définie par
définie par 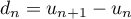 .
.
- Calculer
- On considère la suite arithmétique
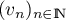 de
raison
de
raison 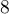 et de premier terme
et de premier terme 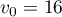 .
.
Justifier que la somme des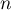 premiers termes de cette suite est
égale à
premiers termes de cette suite est
égale à 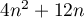 .
.
- Démontrer par récurrence que, pour tout entier naturel
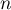 ,
on a:
,
on a:
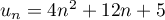
- Valider la conjecture émise à la question 1.b).
Correction exercice 13
(Baccalauréat La Réunion, juin 2008, 5 points)
-
-
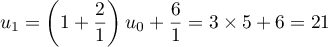 .
.
-
Les premiers termes de la suite
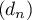 sont:
sont:
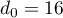 ,
, 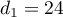 ,
, 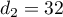 ,
, 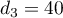 ,
, 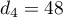 ,
, 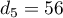 .
A partir de ces premiers termes, on peut conjecturer que
.
A partir de ces premiers termes, on peut conjecturer que  est une suite artithmétique de raison
est une suite artithmétique de raison 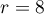 et de premier terme
et de premier terme
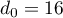 .
.
-
- La somme des
 premiers termes de la suite arithmétique
premiers termes de la suite arithmétique
 est:
est:
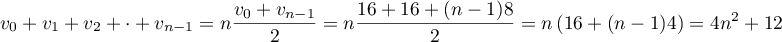 .
.
- Initialisation: pour
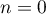 ,
, 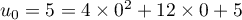 ,
donc la relation est vraie pour
,
donc la relation est vraie pour 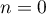 .
Hérédité: Supposons que pour un certain entier
.
Hérédité: Supposons que pour un certain entier 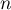 ,
,
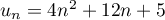 , alors,
, alors,
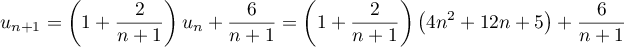 , d'après l'hypothèse de récurrence, et donc,
, d'après l'hypothèse de récurrence, et donc,
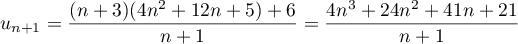 or,
or,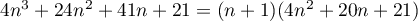 ,
d'où,
,
d'où, 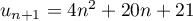 .
.
De plus,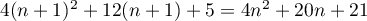 ,
et donc,
,
et donc, 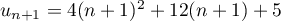 , ce qui montre que
l'expression est encore vraie au rang
, ce qui montre que
l'expression est encore vraie au rang 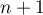 .
.
Conclusion: On vient donc de montrer que, d'après le principe de récurrence, pour tout entier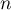 ,
, 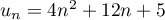 .
.
- Pour tout entier
 ,
,
![$d_n=u_{n+1}-u_n=
\Big[4(n+1)^2+12(n+1)+5\Big]-\Big[4n^2+12n+5\Big]](/Generateur-Devoirs/TS/ChapSuites/ex108.Reunion_c/30.png) ,
soit
,
soit ![$d_n=\Big[4n^2+20n+21\Big]-\Big[4n^2+12n+5\Big]
=8n+16](/Generateur-Devoirs/TS/ChapSuites/ex108.Reunion_c/31.png) , qui est bien l'expression d'une suite arithmétique de
raison 8 et de premier terme
, qui est bien l'expression d'une suite arithmétique de
raison 8 et de premier terme 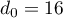 .
.
Cacher la correction
Quelques autres devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
Quelques exercices corrigés
Exercices corrigés
Limites de 2 suites
Exercices corrigés
Limites de 4 suites
Exercices corrigés
Une petite récurrence
Exercices corrigés
Une petite récurrence
Exercices corrigés
Suite auxiliaire géométrique
Voir aussi: