Une petite récurrence

Exercice corrigé - Spécialité maths, terminale générale

Soit 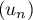$(u_n)$ la suite définie par 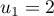$u_1=2$, puis, pour tout entier 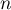$n$ non nul, par la relation de récurrence $u_{n+1}=2-\dfrac1{u_n}$.
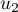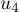  1. Calculer les premiers termes $u_2$, $u_3$ et $u_4$. Donner les résultats sous forme fractionnaire.
  2. Montrer que, pour tout entier $n$ non nul, on a $u_n=\dfrac{n+1}n$.

Correction


Tag:Suites

Autres sujets au hasard: Lancer de dés

Voir aussi:

Quelques devoirs

    Devoir corrigé
    Suites et fonctions - Sujet A
    sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique

    Devoir corrigé
    Suites et fonctions - Sujet B
    sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique

    Devoir corrigé
    Suites et fonctions - Sujet A
    sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe

    Devoir corrigé
    Suites et fonctions - Sujet B
    sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe

    Devoir corrigé
    Suites et fonctions
    maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe


LongPage: h2: 1 - h3: 0