Exponentielle et logarithme: annales de bac et corrections
Terminale générale, spécialité mathématiques
Annales de bac: sujets et corrigés d'exercices posés au baccalauréat en mathématiques sur les fonctions exponentielle et logarithme: dérivées, variations, limites, ...
Exercice 1: Bac 2022: Exponentielle et suite récurrente
Dans le cadre d'un essai clinique on envisage deux protocoles de traiterment de
d'une maladie.
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en mg, par la fonction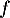 définie sur l'intervalle [0 ; 10] par
définie sur l'intervalle [0 ; 10] par
![\[f(t) = 3t e^{-0,5t+1},\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022/2.png)
où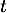 désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqüre intraveineuse, une dose de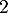 mg de médicament puis à réinjecter toutes les heures une dose de
mg de médicament puis à réinjecter toutes les heures une dose de  mg.
mg.
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de 30 % par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite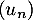 où, pour tout entier naturel
où, pour tout entier naturel 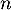 ,
,  désigne la quantité de médicament, exprimée en mg, présente dans le sang du patient immédiatement après l'injection de la
désigne la quantité de médicament, exprimée en mg, présente dans le sang du patient immédiatement après l'injection de la 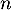 -ième heure. On a donc
-ième heure. On a donc  .
.
Partie A : Étude du premier protocole
Partie B : Étude du deuxième protocole
Cacher la correction
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en mg, par la fonction
où
-
- On admet que la fonction
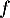 est dérivable sur l'intervalle [0 ; 10] et on note
est dérivable sur l'intervalle [0 ; 10] et on note 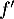 sa fonction dérivée.
Montrer que, pour tout nombre réel
sa fonction dérivée.
Montrer que, pour tout nombre réel  de [0 ; 10], on a:
de [0 ; 10], on a: 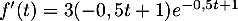 .
.
- En déduire le tableau de variations de la fonction
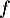 sur l'intervalle [0 ; 10].
sur l'intervalle [0 ; 10].
- Selon cette modélisation, au bout de combien de temps la quantité de médicament présente dans le sang du patient sera-t-elle maximale ? Quelle est alors cette quantité maximale?
- On admet que la fonction
-
- Montrer que l'équation
 admet une unique solution sur l'intervalle [0 ; 2] notée
admet une unique solution sur l'intervalle [0 ; 2] notée 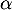 , dont on donnera une valeur approchée à
, dont on donnera une valeur approchée à 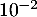 près.
On admet que l'équation
près.
On admet que l'équation 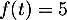 admet une unique solution sur l'intervalle [2 ; 10], notée
admet une unique solution sur l'intervalle [2 ; 10], notée 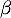 , et qu'une valeur approchée de
, et qu'une valeur approchée de 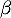 à
à 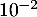 près est 3,46.
près est 3,46.
- On considère que ce traitement est efficace lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à 5 mg. Déterminer, à la minute près, la durée d'efficacité du médicament dans le cas de ce protocole.
- Montrer que l'équation
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqüre intraveineuse, une dose de
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de 30 % par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite
- Calculer, selon cette modélisation, la quantité
 , de médicament (en mg) présente dans le sang du patient immédiatement après l'injection de la première heure.
, de médicament (en mg) présente dans le sang du patient immédiatement après l'injection de la première heure.
- Justifier que, pour tout entier naturel
 , on a :
, on a : 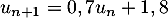 .
.
-
- Montrer par récurrence que, pour tout entier naturel
 , on a :
, on a : 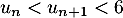 .
.
- En déduire que la suite
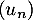 est convergente. On note
est convergente. On note 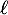 sa limite.
sa limite.
- Déterminer la valeur de
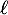 . Interpréter cette valeur dans le contexte de l'exercice.
. Interpréter cette valeur dans le contexte de l'exercice.
- Montrer par récurrence que, pour tout entier naturel
- On considère la suite
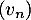 définie, pour tout entier naturel
définie, pour tout entier naturel  , par
, par 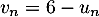 .
.
- Montrer que la suite
 est une suite géométrique de raison
est une suite géométrique de raison  dont on précisera le premier terme.
dont on précisera le premier terme.
- Déterminer l'expression de
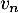 en fonction de
en fonction de 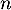 , puis de
, puis de 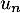 n en fonction de
n en fonction de 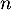 .
.
- Avec ce protocole, on arrête les injections lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à 5,5 mg. Déterminer, en détaillant les calculs, le nombre d'injections réalisées en appliquant ce protocole.
- Montrer que la suite
Correction exercice 1
Partie A : Étude du premier protocole
-
- On a
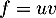 avec
avec 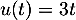 donc
donc 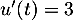 et
et 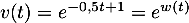 avec
avec
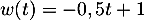 donc
donc 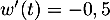 et alors
et alors 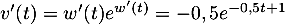 .
.
On obtient alors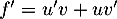 , soit
, soit
![\[\begin{array}{ll}f'(t)&=3e^{-0,5t+1}+3t\tm\lp-0,5e^{-0,5t+1}\rp\\[.4em]
&=3e^{-0,5t+1}\lp1-0,5t\rp\\[.4em]
&=3(-0,5t + 1)e^{-0,5t+1}\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/9.png)
- On a alors le signe de lé dérivée et le sens de variation:
![\[\begin{tabular}{|c|*5c|}\hline
$t$ & 0 && 2 && 10 \\\hline
$-0,5t+1$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
$e^{-0,5t+1}$ && $+$ &\vline & $+$ & \\\hline
$f'(t)$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/10.png)
- Selon cette modélisation, la quantité maximale de médicament présente dans le sang du patient sera de
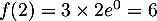 mg, au bout de 2 heures.
mg, au bout de 2 heures.
- On a
-
- Sur [0;2], la fonction
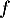 est continue (car même dérivable),
strictement croissante, avec
est continue (car même dérivable),
strictement croissante, avec 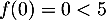 et
et  ,
et ainsi, d'après le théorème des valeurs intermédiaires
(théorème de la bijection), on sait donc qu'il existe une unique
solution
,
et ainsi, d'après le théorème des valeurs intermédiaires
(théorème de la bijection), on sait donc qu'il existe une unique
solution 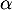 à l'équation
à l'équation 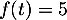 .
.
Avec la calculatrice, par balayage par exemple, on touve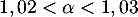 soit,
soit, 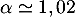 .
.
- On peut compléter le tableau de variation:
![\[\begin{tabular}{|c|*9c|}\hline
$t$ & 0 &&$\alpha$ && 2 &&$\beta$&& 10 \\\hline
&&&&&&&&&\\
$f$&&\psline[arrowsize=8pt]{->}(-.5,-.5)(1.3,.5)&5&&&
\psline[arrowsize=8pt]{->}(-.2,.5)(1.4,-.5)&5&&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/19.png)
grâce auquel on trouve que la durée d'efficacité du médicament est donc de soit 2,44 heures, ou encore 2 heures et 26 minutes.
soit 2,44 heures, ou encore 2 heures et 26 minutes.
- Sur [0;2], la fonction
Partie B : Étude du deuxième protocole
- Selon cette modélisation, à la première heure la quantité dans le sang a diminué de 30%, il en reste donc
 .
On réinjecte de plus une nouvelle dose de 1,8 mg, et on trouve donc que
.
On réinjecte de plus une nouvelle dose de 1,8 mg, et on trouve donc que
![\[u_1=0,7\tm2+1,8=3,2\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/22.png)
- De même que précédemment, à la (n+1)-ème heure,
la quantité dans le sang présente l'heure précédente, soit
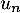 a diminué de 30%, soit
a diminué de 30%, soit 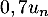 , et on réinjecte, donc ajoute, 1,8 mg.
, et on réinjecte, donc ajoute, 1,8 mg.
On obtient donc bien la relation .
.
-
- Soit la proposition
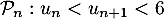 .
.
Initialisation: on a et
et 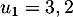 d'où
d'où
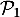 est vraie:
est vraie: 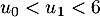 .
.
Hérédité: Supposons que pour un certain entier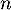 ,
,
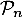 soit vraie, c'est-à-dire
soit vraie, c'est-à-dire
 .
.
Alors, en multipliant par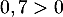 , on obtient
, on obtient
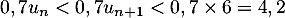 ,
,
puis en ajoutant 1,8 on aboutit à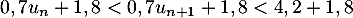 ,
,
c'est-à-dire exactement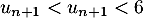 et qui montre donc
et qui montre donc 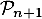 est alors vraie.
est alors vraie.
Conclusion: on vient donc de démontrer, d'après le principe de récurrence, que pour tout entier ,
,
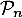 est vraie, c'est-à-dire
est vraie, c'est-à-dire 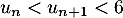 .
.
- On déduit du résultat précédent que la suite
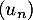 est croissante et aussi qu'elle est majorée par 6.
est croissante et aussi qu'elle est majorée par 6.
On en déduit donc (théorème de convergence monotone) qu'elle converge vers une limite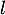 .
.
- On a
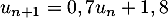 et on sait que
et on sait que  .
.
Ainsi, on doit nécessairement avoir (théorème du point fixe), que
![\[l=0,7l+1,8\iff l=\dfrac{1,8}{0,3}=6\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/46.png)
- Soit la proposition
-
- Pour tout entier
 , on a
, on a
![\[\begin{array}{ll}v_{n+1}&=6-u_{n+1}\\
&=6-\lp0,7u_n+1,8\rp\\
&=4,2-0,7u_n\\
&=0,7\lp6-u_n\right)
=0,7v_n\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/48.png)
ce qui montre que la suite est bien géométrique de raison
est bien géométrique de raison  et de premier terme
et de premier terme  .
.
- On en déduit alors que, pour tout entier
 ,
,
![\[v_n=v_0\times q^n=4\times0,7^n\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/53.png)
puis, comme , que
, que
![\[u_n=6-4\tm0,7^n\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/55.png)
- On arrête les injections lorsque la quantité de médicament
présente dans le sang du patient est supérieure ou égale à 5,5 mg,
soit lorsque
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff&6-4\tm0,7^n\geqslant5,5\\
\iff&-4\tm0,7^n\geqslant-0,5\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/56.png)
soit, en divisant par , puis en prenant le logarithme népérien qui est strictement croissant,
, puis en prenant le logarithme népérien qui est strictement croissant,
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff&0,7^n\leqslant\dfrac{-0,5}{-4}=0,125\\
\iff&\ln\lp0,7^n\rp=n\ln(0,7)\leqslant\ln(0,125)\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/58.png)
Enfin, en divisant par , on obtient finalement
, on obtient finalement
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff n\geqslant\dfrac{\ln(0,125)}{\ln(0,7)}\simeq5,8\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/60.png)
Comme on réalise une injection par heure, il faut donc en réaliser 6.
- Pour tout entier
Cacher la correction
Exercice 2: Bac 2022: Trajectoire d'une balle de golf
Partie A : études de deux fonctions
On considère les deux fonctions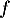 et
et 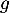 définies sur l'intervalle
définies sur l'intervalle 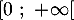 par:
par:
![\[f(x) = 0,06\left(-x^2 +13,7x\right)\quad \text{et}\quad g(x) = (-0,15x + 2,2)e^{0,2x} - 2,2.\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/4.png)
On admet que les fonctions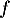 et
et 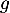 sont dérivables et on note
sont dérivables et on note 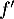 et
et 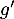 leurs fonctions dérivées respectives.
leurs fonctions dérivées respectives.
Partie B : trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club» de golf.
On souhaite exploiter les fonctions et
et 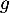 étudiées en Partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
étudiées en Partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
On admettra ici que est la valeur qui annule la fonction
est la valeur qui annule la fonction  et une approximation de la valeur qui annule la fonction
et une approximation de la valeur qui annule la fonction  .
.
On donne ci-dessous les représentations graphiques de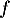 et
et 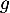 sur l'intervalle [0 ; 13,7].
sur l'intervalle [0 ; 13,7].
![$$(-1,-1)(14,3.5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.2pt]
\psaxes[linewidth=1.25pt,Dx=20,Dy=20]{->}(0,0)(-1,-1)(14,3.5)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}\uput[ur](12,2.2){\blue $\mathcal{C}_g$}
\uput[dl](0,0){0}\uput[d](1,0){1}\uput[l](0,1){1}\uput[d](13.7,0){13,7}
$$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/34.png)
Pour représentant la distance horizontale parcourue par la balle en dizaine de yards après la frappe, (avec
représentant la distance horizontale parcourue par la balle en dizaine de yards après la frappe, (avec  ),
),  (ou
(ou 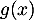 selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaine de yards (1 yard correspond à environ
selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaine de yards (1 yard correspond à environ 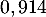 mètre).
mètre).
On appelle « angle de décollage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (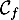 ou
ou 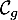 selon le modèle) en son point d'abscisse
selon le modèle) en son point d'abscisse 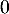 . Une mesure de l'angle de décollage de la balle est
un nombre réel
. Une mesure de l'angle de décollage de la balle est
un nombre réel 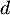 tel que
tel que 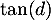 est égal au coefficient directeur de cette tangente.
est égal au coefficient directeur de cette tangente.
De même, on appelle « angle d'atterrissage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (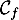 ou
ou 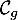 selon le modèle) en son point d'abscisse
selon le modèle) en son point d'abscisse  . Une mesure de l'angle d'atterrissage de la balle est un nombre réel
. Une mesure de l'angle d'atterrissage de la balle est un nombre réel 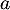 tel que
tel que 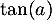 est égal à l'opposé du coefficient directeur de cette tangente.
est égal à l'opposé du coefficient directeur de cette tangente.
Tous les angles sont mesurés en degré.
(-0.3,-0.3)(14,3)
\psplot[plotpoints=1000]{0}{2}{0.822 x mul}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psline(13.7,0)(11,2)
\psarc(0,0){0.7}{0}{40}\rput(1.2,0.5){\footnotesize $d$}
\psarc(13.7,0){0.7}{140}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}&\psset{unit=0.5cm}
\begin{pspicture}(-0.3,-0.75)(14,3.5)
%\psgrid
\psaxes[linewidth=1.25pt,Dx=20,Dy=10](0,0)(-0.3,-0.5)(14,3)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}
\psline(0,0)(10.4,2.8)
\psline(13.7,0)(12,2.9)
\psarc(0,0){1}{0}{20}\rput(2,0.25){\footnotesize $d$}
\psarc(13.7,0){1}{120}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/50.png)
Partie C : interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants:
![\[\begin{tabular}{|*4{p{4.2cm}|}}\hline
Angle de d\'ecollage en degr\'e
&Hauteur maximale en yard
&Angle d'atterrissage en degr\'e
&Distance horizontale en yard au point de chute\\ \hline
24&32&52&137\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/61.png)
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée.
Partie A : études de deux fonctions
Partie B : trajectoires d'une balle de golf
Partie C : interrogation des modèles
Les angles de décollage et d'atterissage sont très clairement différents, et le modèle parabolique de la fonction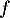 n'est donc clairement pas adapté.
n'est donc clairement pas adapté.
La hauteur maximale est aussi mieux approchée par le second modèle.
Parmi les deux modèles étudiés, le modèle fourni par la fonction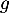 semble donc
le plus adapté.
semble donc
le plus adapté.
Cacher la correction
On considère les deux fonctions
On admet que les fonctions
- On donne le tableau de variations complet de la fonction
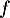 sur l'intervalle
sur l'intervalle 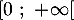 .
.
{$x$} \uput[u](1.6,1.4){$0$} \uput[u](4,1.4){$6,85$} \uput[u](6,1.4){$+ \infty$}
\rput(0.75,0.75){$f(x)$}\uput[u](1.65,0){$0$}\uput[d](4,1.5){$f(6,85)$}\uput[u](6,0){$- \infty$}
\psline{->}(1.9,0.4)(3.2,1.1)\psline{->}(4.8,1.1)(5.7,0.4)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/11.png)
- Justifier la limite de
 en
en  .
.
- Justifier les variations de la fonction
 .
.
- Résoudre l'équation
 .
.
- Justifier la limite de
-
- Déterminer la limite de
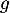 en
en 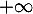 .
.
- Démontrer que, pour tout réel
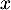 appartenant à
appartenant à 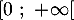 on a :
on a :  .
.
- Étudier les variations de la fonction
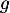 et dresser son tableau de variations sur
et dresser son tableau de variations sur 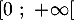 .
.
Préciser une valeur approchée à près du maximum de
près du maximum de 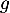 .
.
- Montrer que l'équation
 admet une unique solution non nulle et déterminer, à
admet une unique solution non nulle et déterminer, à  près, une valeur approchée de cette solution.
près, une valeur approchée de cette solution.
- Déterminer la limite de
Partie B : trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club» de golf.
On souhaite exploiter les fonctions
On admettra ici que
On donne ci-dessous les représentations graphiques de
![$$(-1,-1)(14,3.5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.2pt]
\psaxes[linewidth=1.25pt,Dx=20,Dy=20]{->}(0,0)(-1,-1)(14,3.5)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}\uput[ur](12,2.2){\blue $\mathcal{C}_g$}
\uput[dl](0,0){0}\uput[d](1,0){1}\uput[l](0,1){1}\uput[d](13.7,0){13,7}
$$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/34.png)
Pour
On appelle « angle de décollage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (
De même, on appelle « angle d'atterrissage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (
Tous les angles sont mesurés en degré.
(-0.3,-0.3)(14,3)
\psplot[plotpoints=1000]{0}{2}{0.822 x mul}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psline(13.7,0)(11,2)
\psarc(0,0){0.7}{0}{40}\rput(1.2,0.5){\footnotesize $d$}
\psarc(13.7,0){0.7}{140}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}&\psset{unit=0.5cm}
\begin{pspicture}(-0.3,-0.75)(14,3.5)
%\psgrid
\psaxes[linewidth=1.25pt,Dx=20,Dy=10](0,0)(-0.3,-0.5)(14,3)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}
\psline(0,0)(10.4,2.8)
\psline(13.7,0)(12,2.9)
\psarc(0,0){1}{0}{20}\rput(2,0.25){\footnotesize $d$}
\psarc(13.7,0){1}{120}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/50.png)
- Première modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et 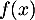 la hauteur correspondante de la balle.
la hauteur correspondante de la balle.
Selon ce modèle :- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
- Vérifier que
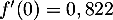 .
.
- Donner une mesure en degré de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
- Quelle propriété graphique de la courbe
 permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
- Seconde modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et  la hauteur correspondante de la balle.
Selon ce modèle :
la hauteur correspondante de la balle.
Selon ce modèle :
- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On précise que
 et
et 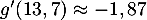 .
.
- Donner une mesure en degré de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
- Justifier que
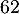 est une valeur approchée, arrondie à l'unité près, d'une mesure en degré de l'angle d'atterrissage de la balle.
est une valeur approchée, arrondie à l'unité près, d'une mesure en degré de l'angle d'atterrissage de la balle.
Tableau : extrait d'une feuille de calcul donnant une mesure en degré d'un angle quand on connait sa tangente :
![\[%\begin{tabularx}{\linewidth}{|c|*{13}{>{\centering \arraybackslash}X|}}
\begin{tabular}{|c|p{2em}|*{12}{c|}}
\hline
&A&B&C&D&E&F&G&H&I&J&K&L&M\\ \hline
1&$\!\!\tan(\theta)$&0,815&0,816&0,817&0,818&0,819&0,82&0,821&0,822&0,823&0,824&0,825&0,826\\ \hline
2&\scriptsize \mbox{$\theta$ en} degr\'es&39,18&39,21&39,25&39,28&39,32&39,35&39,39&39,42&39,45&39,49&39,52&39,56\\ \hline
3& &&&&&&&&&&&&\\ \hline
4&$\!\!\tan(\theta)$&0,285& 0,286& 0,287& 0,288& 0,289&0,29&0,291&0,292&
0,293&0,294&0,295 &0,296\\ \hline
5&\scriptsize \mbox{$\theta$ en} degr\'es&15,91 &15,96&16,01& 16,07& 16,12& 16,17& 16,23& 16,28& 16,33& 16,38& 16,44& 16,49\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/60.png)
- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On précise que
Partie C : interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants:
![\[\begin{tabular}{|*4{p{4.2cm}|}}\hline
Angle de d\'ecollage en degr\'e
&Hauteur maximale en yard
&Angle d'atterrissage en degr\'e
&Distance horizontale en yard au point de chute\\ \hline
24&32&52&137\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/61.png)
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée.
Correction exercice 2
Partie A : études de deux fonctions
-
- On a, pour tout
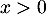 ,
,
![\[f(x)=-0,06x^2\lp1-\dfrac{13,7}x\rp\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/2.png)
avec
![\[\lim_{x\to+\infty}-0,06x^2=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/3.png)
et
![\[\lim_{x\to+\infty}\lp1-\dfrac{13,7}x\rp=1\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/4.png)
d'où, par produit, la limite
![\[\lim_{x\to+\infty}f(x)=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/5.png)
- On a
 d'où le tableau de signes et de variations
d'où le tableau de signes et de variations
![\[\begin{tabular}{|c|*5c|}\hline
$x$ & 0 && 6,85 && $+\infty$ \\\hline
$-2x+13,7$&& $+$ &\zb&$-$&\\\hline
$f'(x)$&& $+$ &\zb&$-$&\\\hline
&&&$f(6,85)$&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/7.png)
- On a
![\[\begin{array}{ll}f(x) = 0&\iff -x^2+13,7x=0\\
&\iff x(-x+13,7)=0\\
&\iff x=0 \text{ ou } x=13,7\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/8.png)
- On a, pour tout
-
- On a
![\[\lim_{x\to+\infty}(-0,15x+2,2)=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/9.png)
et
![\[\lim_{x\to+\infty}e^{0,2x}=+\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/10.png)
et donc, par produit,
![\[\lim_{x\to+\infty}(-0,15x+2,2)e^{0,2x}=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/11.png)
et donc aussi,
![\[\lim_{x\to+\infty}g(x)=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/12.png)
- On a
 avec
avec
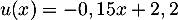 et
et  et
et 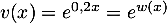 donc
donc
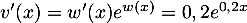 .
.
On obtient donc , soit pour tout
, soit pour tout  ,
,
![\[\begin{array}{ll}g'(x)&=-0,15e^{0,2x}+(-0,15x+2,2)\tm0,2e^{0,2x}\\
&=\Bigl(-0,15+0,2(-0,15x+2,2)\Bigr)e^{0,2x}\\
&=\lp-0,03x+0,29\right) e^{0,2x}
\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/20.png)
- On obtient alors le tableau de signes et de variations:
![\[\begin{tabular}{|c|*5c|}\hline
$x$ & 0 && $29/3$ && $+\infty$ \\\hline
$-0,03x+0,29$&& $+$ &\zb&$-$&\\\hline
$e^{0,2x}$&& $+$ &\vline&$+$&\\\hline
$g'(x)$&& $+$ &\zb&$-$&\\\hline
&&&$g\lp29/3\rp$&&\\
$g$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&0&&&&$-\infty$\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/21.png)
On trouve comme valeur maximale
![\[g\lp\dfrac{29}3\rp\simeq2,98\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/22.png)
- on a pour tout
![$x\in]0;29/3]$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/23.png) ,
, 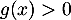 et donc l'équation
et donc l'équation 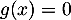 n'admet aucune soltuion.
n'admet aucune soltuion.
Sur , la fonction
, la fonction 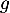 est continue (car même dérivable),
strictement décroissante
avec
est continue (car même dérivable),
strictement décroissante
avec  et
et
 .
.
Ainsi, d'après le théorème des valeurs intermédiaires, ou théorème de la bijection, l'équation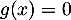 admet une unique solution sur
admet une unique solution sur 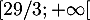 .
.
Finalement, l'équation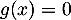 admet une unique solution sur
admet une unique solution sur ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/33.png) , c'est-à-dire une unique solution non nulle.
, c'est-à-dire une unique solution non nulle.
Avec la calculatrice, par balayage ou dichotomie par exemple, on trouve comme valeur approchée de cette solution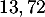 .
.
- On a
Partie B : trajectoires d'une balle de golf
- Première modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et 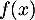 la hauteur correspondante de la balle.
la hauteur correspondante de la balle.
Selon ce modèle :- On a vu que le maximum de
 est
est 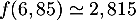 soit une hauteur maximale de 28,15 yards.
soit une hauteur maximale de 28,15 yards.
- On a
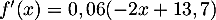 ,
d'où
,
d'où  .
.
-
 est le coefficient directeur de la tangente à la courbe de
est le coefficient directeur de la tangente à la courbe de 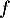 en 0,
c'est-à-dire justement au décollage.
en 0,
c'est-à-dire justement au décollage.
On a donc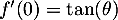 et donc, d'après le tableau donné dans
l'énoncé,
et donc, d'après le tableau donné dans
l'énoncé, 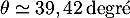 .
.
- La courbe est une parabole. En particulier, elle est symétrique par rapport à la droite
 , abscisse de son sommet.
Les points de décollage
, abscisse de son sommet.
Les points de décollage 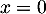 et d'atterissage
et d'atterissage 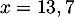 sont symétriques eux aussi par rapport à cette droite, et il en est donc de même des angles
que forment les tangentes à la courbes en ces deux points,
c'est-à-dire que les angles de décollage et d'atterrissage de la balle sont
égaux.
sont symétriques eux aussi par rapport à cette droite, et il en est donc de même des angles
que forment les tangentes à la courbes en ces deux points,
c'est-à-dire que les angles de décollage et d'atterrissage de la balle sont
égaux.
- On a vu que le maximum de
- Seconde modélisation
- D'après ce modèle, la hauteur maximale est
![\[g\lp\dfrac{29}3\rp\simeq2,98\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/48.png)
soit 29,8 yard. On précise que et .
.
-
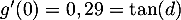 soit, d'après le tableau foruni,
soit, d'après le tableau foruni, 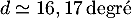 .
.
- De même pour l'angle d'atterissage,
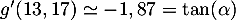 soit
soit 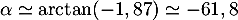 soit,
arrondie à l'unité près, environ 62 degrés.
soit,
arrondie à l'unité près, environ 62 degrés.
- D'après ce modèle, la hauteur maximale est
Partie C : interrogation des modèles
Les angles de décollage et d'atterissage sont très clairement différents, et le modèle parabolique de la fonction
La hauteur maximale est aussi mieux approchée par le second modèle.
Parmi les deux modèles étudiés, le modèle fourni par la fonction
Cacher la correction
Exercice 3: Bac 2021, sujet 0 - Logarithme et convexité
Sur le graphique ci-dessous, on a représenté dans un repère orthonormé :
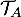 est parallèle à l’axe des abscisses. La droite
est parallèle à l’axe des abscisses. La droite 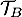 coupe l’axe des abscisses au point de coordonnées (3 ; 0) et l’axe des ordonnées au point de coordonnées (0 ; 3).
coupe l’axe des abscisses au point de coordonnées (3 ; 0) et l’axe des ordonnées au point de coordonnées (0 ; 3).
(\n,3.5)}
%\multido{\n=0+1}{51}{\psline[linewidth=0.3pt](\n,-100)(\n,100)}
\multido{\n=-0.5+0.5}{8}{\psline[linewidth=0.35pt,linecolor=lightgray](0,\n)(7.50,\n) }
\psaxes[linewidth=0.95pt,Dx=0.5,Dy=0.5]{->}(0,0)(0,-0.5)(7.6,3.6)
\psaxes[linewidth=0.95pt,Dx=0.5,Dy=0.5](0,0)(0,-0.5)(7.6,3.6)
\psplot[linewidth=1.25pt,linecolor=blue,plotpoints=5000]{0.127}{7.50}{x ln 2 add x div}
\psplot[linewidth=0.85pt,linecolor=cyan,plotpoints=5000]{-0.1}{7.50}{2.71828}
\psplot[linewidth=0.85pt,linecolor=cyan,plotpoints=5000]{-0.1}{3.50}{x neg 3 add}
\psdots[dotstyle=Bullet,dotscale =1.1](0.367879,2.71828)(1,2)
\uput[ur](0.468,2.81828){A}\uput[ur](1.1,2.1){B}
\uput[u](6.5,2.5){\cyan $\mathcal{T}_A$}
\uput[r](2.2,0.5){\cyan $\mathcal{T}_B$}
\uput[r](5,0.5) {\blue $\mathcal{C}_f$}
$$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/11.png)
On note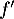 la fonction dérivée de
la fonction dérivée de  .
.
Partie I
Partie II
On suppose maintenant que la fonction est définie sur
est définie sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/18.png) par :
par :
![\[f(x) =\dfrac{2+\ln(x)}{x}.\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/19.png)
Partie I
Partie II
 ,
pour
,
pour 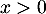
Cacher la correction
- la courbe représentative
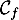 d’une fonction
d’une fonction 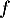 définie et dérivable sur
définie et dérivable sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/3.png) ;
;
- la tangente
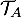 à la courbe
à la courbe 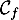 au point A de coordonnées
au point A de coordonnées 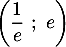 ;
;
- la tangente
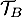 à la courbe
à la courbe 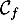 au point B de coordonnées (1 ; 2).
au point B de coordonnées (1 ; 2).
(\n,3.5)}
%\multido{\n=0+1}{51}{\psline[linewidth=0.3pt](\n,-100)(\n,100)}
\multido{\n=-0.5+0.5}{8}{\psline[linewidth=0.35pt,linecolor=lightgray](0,\n)(7.50,\n) }
\psaxes[linewidth=0.95pt,Dx=0.5,Dy=0.5]{->}(0,0)(0,-0.5)(7.6,3.6)
\psaxes[linewidth=0.95pt,Dx=0.5,Dy=0.5](0,0)(0,-0.5)(7.6,3.6)
\psplot[linewidth=1.25pt,linecolor=blue,plotpoints=5000]{0.127}{7.50}{x ln 2 add x div}
\psplot[linewidth=0.85pt,linecolor=cyan,plotpoints=5000]{-0.1}{7.50}{2.71828}
\psplot[linewidth=0.85pt,linecolor=cyan,plotpoints=5000]{-0.1}{3.50}{x neg 3 add}
\psdots[dotstyle=Bullet,dotscale =1.1](0.367879,2.71828)(1,2)
\uput[ur](0.468,2.81828){A}\uput[ur](1.1,2.1){B}
\uput[u](6.5,2.5){\cyan $\mathcal{T}_A$}
\uput[r](2.2,0.5){\cyan $\mathcal{T}_B$}
\uput[r](5,0.5) {\blue $\mathcal{C}_f$}
$$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/11.png)
On note
Partie I
- Déterminer graphiquement les valeurs de
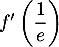 et de
et de 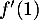 .
.
- En déduire une équation de la droite
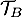 .
.
Partie II
On suppose maintenant que la fonction
- Par le calcul, montrer que la courbe
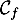 passe par les points A et B et qu’elle coupe l’axe des abscisses en un point unique que l’on précisera.
passe par les points A et B et qu’elle coupe l’axe des abscisses en un point unique que l’on précisera.
- Déterminer la limite de
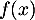 quand
quand 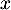 tend vers 0 par valeurs supérieures, et la limite de
tend vers 0 par valeurs supérieures, et la limite de 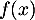 quand
quand 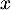 tend vers
tend vers 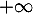 .
.
- Montrer que, pour tout
![$x\in]0~;~\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/26.png) ,
,
![\[f'(x)=\dfrac{-1-\ln(x)}{x^2} .\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/27.png)
- Dresser le tableau de variations de
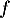 sur
sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/29.png) .
.
- On note
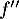 la fonction dérivée seconde de
la fonction dérivée seconde de 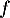 On admet que, pour tout
On admet que, pour tout ![$x\in]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/32.png)
![\[f''(x)=\dfrac{1+2\ln(x)}{x^3} .\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/33.png)
Déterminer le plus grand intervalle sur lequel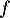 est convexe.
est convexe.
Correction exercice 3
Partie I
-
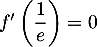 car c'est le coefficient directeur de la tangente
car c'est le coefficient directeur de la tangente
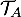 , qui est horizontale.
, qui est horizontale.
De même, est le coefficient directeur de la tangente
est le coefficient directeur de la tangente
 , qui passe par le point
, qui passe par le point 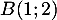 et le point
de l'axe des abscisses de coordonnées
et le point
de l'axe des abscisses de coordonnées 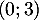 .
.
Ce coefficient directeur est donc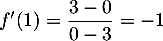 .
.
- La droite
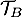 a pour coefficient directeur
a pour coefficient directeur 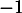 et 3 pour ordonnée à l'origine, donc elle a pour équation:
et 3 pour ordonnée à l'origine, donc elle a pour équation: 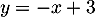 .
.
Partie II
-
-
![\[f\lp\dfrac1e\right) = \dfrac{2+\ln\lp\frac1e\right)}{\frac1e}
= e\left( 2 - \ln(e)\right) = e( 2 - 1)=e\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/13.png)
donc .
.
-
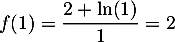 donc
donc 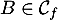 .
.
- La courbe
 coupe l'axe des abscisses en un point dont l'abscisse est solution de l'équation
coupe l'axe des abscisses en un point dont l'abscisse est solution de l'équation  , soit,
, soit,
![\[\begin{array}{ll}f(x)=0
&\iff \dfrac{2+\ln(x)}{x} = 0\\
&\iff 2+\ln(x)=0\\
&\iff \ln(x)=-2\\
&\iff x = e^{-2}
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/19.png)
Donc la courbe coupe l'axe des abscisses en un point unique de coordonnées
coupe l'axe des abscisses en un point unique de coordonnées 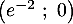 .
.
-
-
On a
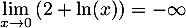 et
et 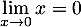 , avec
, avec 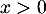 , d'où, par quotient des limites,
, d'où, par quotient des limites,
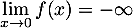 .
.
On a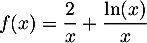 ,
avec
,
avec
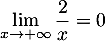 et, par croissances comparées,
et, par croissances comparées,
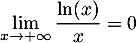
d'où,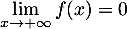 .
.
- Pour
 , en dérivant le quotient
, en dérivant le quotient  , on a
, on a
![\[\begin{array}{ll}f'(x)&=\dfrac{\frac1x\times x - (2+\ln(x)) \times1}{x^2} \\[.8em]
&= \dfrac{1-2-\ln(x)}{x^2} = \dfrac{-1-\ln(x)}{x^2}
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/32.png)
- On a
On dresse le tableau de variations de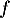 sur
sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/35.png) :
:
![\[\renewcommand{\arraystretch}{1.3}
\psset{nodesep=3pt,arrowsize=2pt 3}% param\`etres
\def\esp{\hspace*{2.5cm}}% pour modifier la largeur du tableau
\def\hauteur{0pt}% mettre au moins 20pt pour augmenter la hauteur
\begin{array}{|c|l *4{c}|}
\hline
x & 0 & \esp & e^{-1} & \esp & +\infty \\
\hline
-1-\ln(x)&\vline\;\vline & + & \vline\hspace{-2.7pt}0 & - & \\ \hline
x^2 &0 && + & & \\\hline
f'(x) &\vline\;\vline & \pmb{+} & \vline\hspace{-2.7pt}0 & \pmb{-} & \\
\hline
& \vline\;\vline & & \Rnode{max}{e} & & \\
f(x) &\vline\;\vline & & & & \rule{0pt}{\hauteur} \\
& \vline\;\vline \Rnode{min1}{~-\infty} & & & & \Rnode{min2}{0} \rule{0pt}{\hauteur}
\ncline{->}{min1}{max}
\ncline{->}{max}{min2}
\\
\hline\end{array}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/36.png)
- La fonction
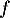 est convexe lorsque
est convexe lorsque 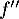 est positive,
soit
est positive,
soit
![\[\begin{array}{ll}f''(x)\geqslant 0
&\iff \dfrac{1+2\ln(x)}{x^3} \geqslant 0\\[.8em]
&\iff 1+2\ln(x) \geqslant 0\\[.6em]
&\iff \ln(x) \geqslant -\dfrac12\\
&\iff x\geqslant e^{-\frac{1}{2}}
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/39.png)
Donc le plus grand intervalle sur lequel la fonction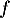 est convexe est
est convexe est 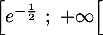 .
.
Cacher la correction
Exercice 4: Bac 2021 - Exponentielle et logarithme
Soit 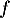 la fonction définie sur l'intervalle
la fonction définie sur l'intervalle ![$]0~;~ +\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1/2.png) par :
par :
![\[f(x) = \dfrac{e^x}x\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1/3.png)
On note la courbe représentative de la fonction
la courbe représentative de la fonction 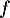 dans un repère orthonormé.
dans un repère orthonormé.
(Bac 15 mars 2021 - sujet 1)
Soit la fonction définie sur l'intervalle
la fonction définie sur l'intervalle ![$]0~;~ +\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1_c/2.png) par :
par :
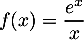 .
.
On note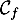 la courbe représentative de la fonction
la courbe représentative de la fonction  dans un repère orthonormé.
dans un repère orthonormé.
Cacher la correction
On note
-
- Préciser la limite de la fonction
 en
en  .
.
- Justifier que l'axe des ordonnées est asymptote à
la courbe
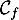 .
.
- Préciser la limite de la fonction
- Montrer que, pour tout nombre réel
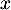 de l'intervalle
de l'intervalle
![$]0~;~ +\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1/10.png) , on a :
, on a :
![\[f'(x)=\dfrac{e^x(x - 1)}{x^2}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1/11.png)
où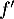 désigne la fonction dérivée de la fonction
désigne la fonction dérivée de la fonction 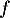 .
.
- Déterminer les variations de la fonction
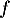 sur l'intervalle
sur l'intervalle ![$]0~;~ +\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1/15.png) .
.
On établira un tableau de variations de la fonction dans lequel apparaîtront les limites.
dans lequel apparaîtront les limites.
- Soit
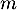 un nombre réel. Préciser, en fonction des valeurs du nombre réel
un nombre réel. Préciser, en fonction des valeurs du nombre réel 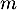 , le nombre de solutions de l'équation
, le nombre de solutions de l'équation  .
.
- On note
 la droite d'équation
la droite d'équation 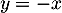 .
.
On note A un éventuel point de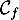 d'abscisse
d'abscisse 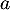 en lequel la tangente à la courbe
en lequel la tangente à la courbe 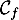 est parallèle à la droite
est parallèle à la droite  .
.
- Montrer que
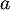 est solution de l'équation
est solution de l'équation 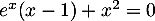 .
.
On note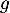 la fonction définie sur
la fonction définie sur 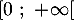 par
par 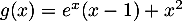 .
.
On admet que la fonction est dérivable et on note
est dérivable et on note 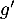 sa fonction dérivée.
sa fonction dérivée.
- Calculer
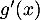 pour tout nombre réel
pour tout nombre réel 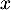 de l'intervalle
de l'intervalle
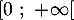 , puis dresser le tableau de variations de
, puis dresser le tableau de variations de 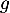 sur
sur 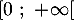 .
.
- Montrer qu'il existe un unique point
 en lequel la tangente
à
en lequel la tangente
à 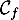 est parallèle à la droite
est parallèle à la droite  .
.
- Montrer que
Correction exercice 4
(Bac 15 mars 2021 - sujet 1)
Soit
On note
-
- D'après le théorème de croissances comparées, on a
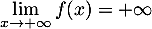 .
.
- On cherche la limite de
 en 0.
On a
en 0.
On a  d'où, par quotient de limites,
d'où, par quotient de limites,
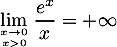 ,
ce qui montre que l'axe des ordonnées est asymptote verticale à la
courbe
,
ce qui montre que l'axe des ordonnées est asymptote verticale à la
courbe  .
.
- D'après le théorème de croissances comparées, on a
- Pour tout réel
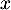 de l'intervalle
de l'intervalle ![$]0~;~ +\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1_c/12.png) , on a,
en dérivant le quotient
, on a,
en dérivant le quotient 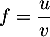 ,
,
![\[f'(x)=\dfrac{e^{x}\times x - e^x\times1}{x^2} = \dfrac{e^x(x-1)}{x^2}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1_c/14.png)
- On cherche le signe de
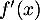 , pour obtenir les variations de
, pour obtenir les variations de  ,
,
![\[\renewcommand{\arraystretch}{1.5}
\begin{array}{|c | *{6}{c} |}
\hline
x && 0 & \hspace*{2cm} & 1 & \hspace*{2cm} & +\infty \\
\hline
x-1 && & - & \vline\hspace{-2.7pt}{0} & + & \\
\hline
e^{x} && & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \\
\hline
x^2 & 0& \hfill{} & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \\
\hline
f'(x) & \vline\;\vline& & - & \vline\hspace{-2.7pt}{0} &+& \\
\hline
& \vline\;\vline\;& +\infty & & & & +\infty \\
f(x) & \vline\;\vline\;& &
\psline[arrowsize=8pt]{->}(-1,.6)(1,-.6)& &
\psline[arrowsize=8pt]{->}(-1,-.6)(1,.6) & \\
& \vline\;\vline\;& & & e & &
\\
\hline
\end{array}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1_c/17.png)
avec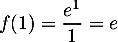
- D'après le tableau de variations et le théorème des valeurs
intermédiaires,
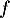 étant continue sur
étant continue sur 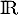 et strictement décroissante
sur
et strictement décroissante
sur ![$]0;1[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1_c/21.png) et strictement croissante sur
et strictement croissante sur 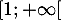 , on a
, on a
- si
 , l'équation
, l'équation  n'admet pas de solution;
n'admet pas de solution;
- si
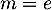 , l'équation
, l'équation 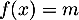 admet une solution unique
admet une solution unique  ;
;
- si
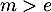 , l'équation
, l'équation 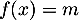 admet deux solutions.
admet deux solutions.
- si
-
- La tangente en
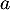 est parallèle à la droite
est parallèle à la droite  si et seulement si le coefficient directeur de la tangente est égal à
si et seulement si le coefficient directeur de la tangente est égal à
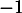 , autrement dit quand
, autrement dit quand 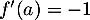 , et donc
, et donc
![\[\begin{array}{ll}f'(a)=-1
&\iff \dfrac{e^a(a-1)}{a^2}=-1\\
&\iff e^a(x-1) = -a^2\\
&\iff e^{a}(x-1)+a^2=0
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1_c/34.png)
ce qui veut dire que le nombre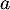 est solution de l'équation
est solution de l'équation  .
.
-
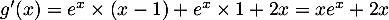
Sur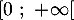 on a
on a 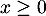 et
et 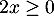 ainsi que
ainsi que  d'où
d'où
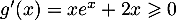 .
.
On dresse alors le tableau de variations
![\[
{\renewcommand{\arraystretch}{1.3}
\begin{array}{|c| *3{c}|}
\hline
x & 0 & \hspace*{2cm} & +\infty \\
\hline
g'(x) & 0 &+& \\
\hline
& & &\\
g(x) & & \psline[arrowsize=8pt]{->}(-1,-.6)(1,.6)
& \\
& -1 & & \\
\hline
\end{array}
}
\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1_c/43.png)
- On a, comme
 et par produit et somme de
limite,
et par produit et somme de
limite, 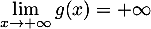 .
.
Ainsi, comme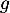 est continue sur
est continue sur 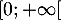 , strictement croissante,
et que
, strictement croissante,
et que 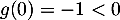 et avec la limite précédente, on a,
d'après le téorème de la bijection (ou théorème des valeurs intermédiaires),
qu'il existe une unique solution
et avec la limite précédente, on a,
d'après le téorème de la bijection (ou théorème des valeurs intermédiaires),
qu'il existe une unique solution  à l'équation
à l'équation  ,
et donc il existe un unique point A en lequel la tangente à
,
et donc il existe un unique point A en lequel la tangente à
 est parallèle à la droite
est parallèle à la droite  .
.
- La tangente en
Cacher la correction
Exercice 5: Bac 2021 - Logarithme, limites et convexité
On considère la fonction 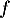 définie sur l'intervalle
définie sur l'intervalle ![$]0~;~ +\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx/2.png) par :
par :
![\[f(x) = x + 4 - 4 \ln (x) - \dfrac3x\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx/3.png)
où ln désigne la fonction logarithme népérien.
On note la représentation graphique de
la représentation graphique de 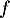 dans un repère orthonormé.
dans un repère orthonormé.
Cacher la correction
où ln désigne la fonction logarithme népérien.
On note
- Déterminer la limite de la fonction
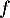 en
en 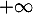 .
.
- On admet que la fonction
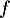 est dérivable sur
est dérivable sur ![$]0~;~ +\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx/9.png) et on note
et on note 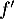 sa fonction dérivée.
sa fonction dérivée.
Démontrer que, pour tout nombre réel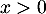 , on a :
, on a :
![\[f'(x) = \dfrac{x^2 - 4x + 3}{x^2}.\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx/12.png)
-
- Donner le tableau de variations de la fonction
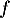 sur l'intervalle
sur l'intervalle ![$]0~;~ +\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx/14.png) .
On y fera figurer les valeurs exactes des extremums et les limites de
.
On y fera figurer les valeurs exactes des extremums et les limites de 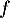 en
en 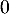 et en
et en 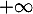 .
On admettra que
.
On admettra que 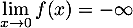 .
.
- Par simple lecture du tableau de variations, préciser le nombre de solutions de l'équation
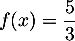 .
.
- Donner le tableau de variations de la fonction
- Étudier la convexité de la fonction
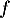 c'est-à-dire préciser les parties de l'intervalle
c'est-à-dire préciser les parties de l'intervalle ![$]0~;~ +\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx/21.png) sur lesquelles
sur lesquelles 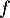 est convexe, et celles sur lesquelles
est convexe, et celles sur lesquelles 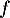 est concave.
est concave.
On justifiera que la courbe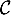 admet un unique point d'inflexion, dont on précisera les coordonnées.
admet un unique point d'inflexion, dont on précisera les coordonnées.
Correction exercice 5
- En
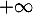 ,
,
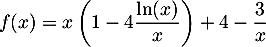
avec par croissances comparées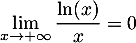 donc
donc 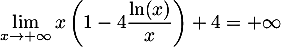
et donc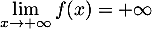
-
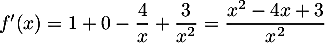
-
- Le trinôme du second degré au numérateur
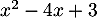 a pour discriminant
a pour discriminant 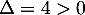 et admet donc deux racines distinctes
et admet donc deux racines distinctes
 et
et 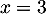 et alors
et alors
![\[\renewcommand{\arraystretch}{1.5}
\begin{array}{|c | l *{6}{c} |}
\hline
x & 0 & \hspace*{2cm} & 1 & \hspace*{2cm} & 3 & \hspace*{2cm} & +\infty \\
\hline
x^2-4x+3 & &+& \vline\hspace{-2.7pt}{0} &- & \vline\hspace{-2.7pt}{0} &- &\\
\hline
x^2 & 0 &+ & \vline\hspace{-2.7pt}{\phantom 0} &+ & \vline\hspace{-2.7pt}{\phantom 0} &+ &\\
\hline
f'(x) & \vline\;\vline &+& \vline\hspace{-2.7pt}{0} &- & \vline\hspace{-2.7pt}{0} &+ & \\
\hline
& \vline\;\vline\; & & \Rnode{max1}{2} & & & & \Rnode{max2}{+\infty} \\
f (x) &\vline\;\vline\; & & & & & &\\
&\vline\;\vline\; \Rnode{min1}{-\infty} & & & & \Rnode{min2}{6-4\ln(3)\approx 1,61} & &
\ncline{->}{min1}{max1}
\ncline{->}{max1}{min2}
\ncline{->}{min2}{max2} \\
\hline
\end{array}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx_c/11.png)
avec les valeurs particulières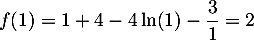 ;
;
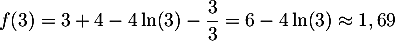
- D'après le tableau de variations, l'équation
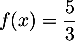 admet une solution dans
admet une solution dans ![$]0;1[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx_c/15.png) , une dans
, une dans ![$]1;3[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx_c/16.png) et enfin
une dans
et enfin
une dans ![$]3;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx_c/17.png) car
car 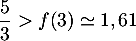
Cette équation admet donc trois solutions dans![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx_c/19.png) .
.
- Le trinôme du second degré au numérateur
- La convexité de
 est donnée par le signe de la dérivée seconde:
est donnée par le signe de la dérivée seconde:
![\[f'(x)=\dfrac{x^2-4x+3}{x^2}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx_c/21.png)
donc
![\[\begin{array}{ll}f''(x) &= \dfrac{(2x-4)\times x^2 - (x^2-4x+3)\times2x}{x^4}\\
&= \dfrac{(2x^2 -4x -2x^2 +8x -6)\times x}{x^4}\\
&=\dfrac{4x-6}{x^3}\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx_c/22.png)
![\[\renewcommand{\arraystretch}{1.5}
\begin{array}{|c | l *{4}{c} |}
\hline
x & 0 & \hspace*{2cm} & \frac{3}{2} & \hspace*{2cm} & +\infty \\
\hline
4x-6 & & - & \vline\hspace{-2.7pt}{0} & + & \\
\hline
x^3 &0 & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \\
\hline
f''(x) &\vline\;\vline & - & \vline\hspace{-2.7pt}{0} & + & \\
\hline
&\vline\;\vline & f \text{ concave} & \vline\hspace{-2.7pt}{\phantom0} & f \text{ convexe} & \\
\hline
\end{array}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-1-log-cvx_c/23.png)
La dérivée seconde s'annule et change de signe pour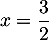 donc la courbe
donc la courbe  admet un unique point d'inflexion
d'abscisse
admet un unique point d'inflexion
d'abscisse  .
.
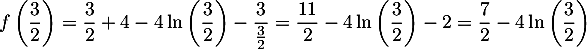
La courbe admet donc un unique point d'inflexion de coordonnées
admet donc un unique point d'inflexion de coordonnées
 .
.
Cacher la correction
Exercice 6: Bac 2023 - Logarithme, variation, limites et TVI
On considère la fonction  définie sur
définie sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323/2.png) par
par
![\[f(x) = x^2 - 8\ln (x)\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323/3.png)
où ln désigne la fonction logarithme népérien.
On admet que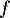 est dérivable sur
est dérivable sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323/5.png) , on note
, on note 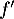 sa fonction dérivée.
sa fonction dérivée.
(Bac spécialité maths, 20 mars 2023)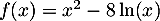 pour
pour ![$x\in]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323_c/2.png)
Cacher la correction
où ln désigne la fonction logarithme népérien.
On admet que
- Déterminer
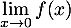 .
.
- On admet que, pour tout
 ,
,  .
.
En déduire la limite: .
.
- Montrer que, pour tout réel
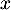 de
de ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323/12.png) ,
,  .
.
- Étudier les variations de
 sur
sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323/15.png) et dresser son tableau de variations complet.
et dresser son tableau de variations complet.
On précisera la valeur exacte du minimum de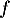 sur
sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323/17.png) .
.
- Démontrer que, sur l'intervalle ]0 ; 2], l'équation
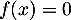 admet une solution
unique
admet une solution
unique 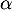 (on ne cherchera pas à déterminer la valeur de
(on ne cherchera pas à déterminer la valeur de 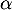 ).
).
- On admet que, sur l'intervalle
 , l'équation
, l'équation  admet une solution unique
admet une solution unique  (on ne cherchera pas à déterminer la valeur de
(on ne cherchera pas à déterminer la valeur de 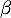 ).
).
En déduire le signe de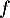 sur l'intervalle
sur l'intervalle ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323/26.png) .
.
- Pour tout nombre réel
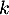 , on considère la fonction
, on considère la fonction 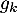 définie sur
définie sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323/29.png) par:
par:
![\[g_k(x) = x^2 - 8\ln (x) + k.\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323/30.png)
En s'aidant du tableau de variations de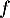 , déterminer la plus petite valeur de
, déterminer la plus petite valeur de 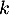 pour laquelle la fonction
pour laquelle la fonction  est positive sur l'intervalle
est positive sur l'intervalle ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323/34.png) .
.
Correction exercice 6
(Bac spécialité maths, 20 mars 2023)
-
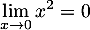 et
et
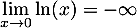 d'où, par soustraction des limites,
d'où, par soustraction des limites,
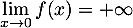 .
.
-
 et, par croissances comparées,
et, par croissances comparées,
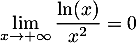 , d'où par produit des limites,
, d'où par produit des limites,
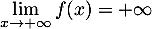 .
.
- On a, pour tout réel
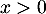 ,
,
![\[f'(x) = 2x-8\tm\dfrac1x=\dfrac{2x^2-8}x=\dfrac{2\left( x^2 - 4\right)}{x}\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323_c/10.png)
- Le numérateur de
 est un trinôme du second degré de racines évidentes
est un trinôme du second degré de racines évidentes  et
et 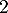 , et on a donc
, et on a donc
![\[\begin{tabular}{|c|lcccc|}\hline
$x$ & 0 &&$2$ && $+\infty$ \\\hline
$x^2-4$ && $-$ &\zb&$+$&\\\hline
$x$ &0& $+$ &$|$&$+$&\\\hline
$f'(x)$ && $-$ &\zb&$+$&\\\hline
&\ $+\infty$&&&&$+\infty$\\
$f$&\psline(0,-.7)(0,1.4)\,\psline(0,-.7)(0,1.4)&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&$4-8\ln(2)$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323_c/14.png)
Le minimum de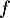 sur
sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323_c/16.png) est
est  atteint en
atteint en 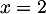 .
.
- Sur l'intervalle ]0 ; 2],
 est continue et strictement décroissante,
avec
est continue et strictement décroissante,
avec 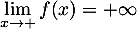 et
et 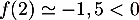 .
.
On en déduit, d'après le théorème de la bijection (ou théorème des valeurs intermédaires version forte) que l'équation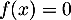 admet une unique solution
admet une unique solution  sur cet intervalle.
sur cet intervalle.
- On complète le tableau de variation précédent en y ajoutant
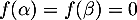 , et on en déduit le signe de
, et on en déduit le signe de  :
:
![\[\begin{tabular}{|c|lcccccccc|}\hline
$x$ & 0 &$\alpha$& &&$2$ && $\beta$ && $+\infty$ \\\hline
&\ $+\infty$&&&&&&&&$+\infty$\\
$f$&\psline(0,-1.2)(0,.9)\,\psline(0,-1.2)(0,.9)
&\psline[arrowsize=7pt]{->}(-.4,.5)(1.1,-.4)0&&&&\psline[arrowsize=7pt]{->}(-.4,-.4)(1.3,.5)&0&&\\
&&&&&$4-8\ln(2)$&&&&\\\hline
$f(x)$&\ $+$&0&&&$-$&&0&$+$&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323_c/26.png)
- Pour tout nombre réel
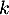 , on a
, on a
![\[g_k(x) = x^2 - 8\ln (x) + k = f(x) + k\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323_c/28.png)
On a vu précédemment que, pour tout , on a
, on a
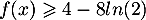 et ainsi,
et ainsi,
![\[g_k(x)=f(x)+k\geqslant4-8ln(2)+k\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac200323_c/31.png)
Pour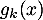 soit positive pour tout
soit positive pour tout 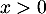 , il faut et suffit donc de choisir
, il faut et suffit donc de choisir
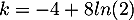
Cacher la correction
Exercice 7: Bac 2021 - Exponentielles, distance entre deux courbes
Le graphique suivant représente, dans un repère orthogonal, les courbes
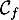 et
et 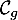 des fonctions
des fonctions  et
et  définies sur
définies sur 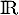 par:
par:
![\[f(x) = x^2e^{-x}\quad \text{ et } \quad g(x) = e^{-x}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/6.png)
(2.5,\n)}
\multido{\n=-2+1}{5}{\psline[linewidth=0.1pt,linestyle=dashed](\n,-1)(\n,9)}
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle,Dy=2]{->}(0,0)(-2.5,-1)(2.5,9)
\psplot[linewidth=1.5pt,linecolor=blue,plotpoints=2000]{-2.5}{2.5}{x dup mul 2.71828 x exp div}
\psplot[linewidth=1.5pt,linecolor=red,plotpoints=2000]{-2.5}{2.5}{2.71828 x neg exp}
\psline[linestyle=dashed,linewidth=1.25pt](-0.6,-1)(-0.6,9)
\psdots(-0.6,0.656)(-0.6,1.822)
\uput[r](-0.6,0.656){\footnotesize $N$}\uput[r](-0.6,1.822){\footnotesize $M$}
\uput[r](-1.4,7){\blue $\mathcal{C}_f$}\uput[l](-2.1,7.4){\red $\mathcal{C}_g$}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/7.png)
Cacher la correction
(2.5,\n)}
\multido{\n=-2+1}{5}{\psline[linewidth=0.1pt,linestyle=dashed](\n,-1)(\n,9)}
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle,Dy=2]{->}(0,0)(-2.5,-1)(2.5,9)
\psplot[linewidth=1.5pt,linecolor=blue,plotpoints=2000]{-2.5}{2.5}{x dup mul 2.71828 x exp div}
\psplot[linewidth=1.5pt,linecolor=red,plotpoints=2000]{-2.5}{2.5}{2.71828 x neg exp}
\psline[linestyle=dashed,linewidth=1.25pt](-0.6,-1)(-0.6,9)
\psdots(-0.6,0.656)(-0.6,1.822)
\uput[r](-0.6,0.656){\footnotesize $N$}\uput[r](-0.6,1.822){\footnotesize $M$}
\uput[r](-1.4,7){\blue $\mathcal{C}_f$}\uput[l](-2.1,7.4){\red $\mathcal{C}_g$}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/7.png)
-
- Déterminer les coordonnées des points d'intersection de
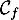 et
et 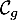 .
.
- Étudier la position relative des courbes
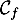 et
et 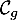 .
.
- Déterminer les coordonnées des points d'intersection de
- Pour tout nombre réel
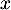 de l'intervalle
de l'intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/13.png) ,
on considère les points
,
on considère les points 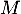 de coordonnées
de coordonnées 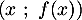 et
et 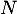 de coordonnées
de coordonnées 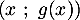 , et on note
, et on note 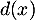 la distance
la distance 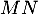 .
On admet que :
.
On admet que :  .
.
On admet que la fonction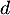 est dérivable sur l'intervalle
est dérivable sur l'intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/22.png) et on note
et on note 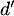 sa fonction dérivée.
sa fonction dérivée.
- Montrer que
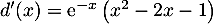 .
.
- En déduire les variations de la fonction
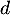 sur l'intervalle
sur l'intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021/26.png) .
.
- Déterminer l'abscisse commune
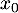 des points
des points  et
et 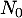 permettant d'obtenir une distance
permettant d'obtenir une distance 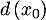 maximale, et donner une valeur approchée à
maximale, et donner une valeur approchée à 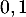 près de la distance
près de la distance 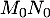 .
.
- Montrer que
- Soit
 la droite d'équation
la droite d'équation 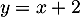 .
.
On considère la fonction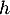 dérivable sur
dérivable sur 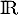 et définie par:
et définie par:
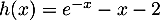 .
.
En étudiant le nombre de solutions de l'équation ,
déterminer le nombre de points d'intersection de la droite
,
déterminer le nombre de points d'intersection de la droite  et de la courbe
et de la courbe 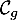 .
.
Correction exercice 7
-
- Les abscisses des points d'intersection de
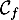 et
et 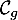 sont les points d'abscisses
sont les points d'abscisses 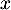 solutions de l'équation
solutions de l'équation 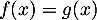 ,
soit
,
soit
![\[f(x)=g(x) \iff x^2e^{-x}=e^{-x}\iff (x^2-1)e^{-x}=0\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/5.png)
Pour tout réel ,
, 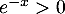 donc en particulier
donc en particulier 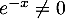 ,
et alors
,
et alors
![\[f(x)=g(x) \iff x^2-1=0 \iff x=-1 \text{ ou } x=1\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/9.png)
Pour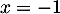 ,
, 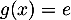 , et pour
, et pour  ,
, 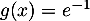 .
.
Les coordonnées des points d'intersection sont donc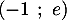 et
et 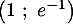 .
.
- Étudier la position relative de
 et
et 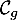 , revient à étudier le signe de
la différence
, revient à étudier le signe de
la différence 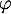 définie par
définie par
![\[\varphi(x)=f(x)-g(x)=(x^2-1)e^{-x}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/19.png)
soit
![\[\renewcommand{\arraystretch}{1.5}
\def\esp{\hspace*{1cm}}
\begin{array}{|c | *7{c} |}
\hline
x & -\infty & \esp & -1 & \esp & 1 & \esp & +\infty \\\hline
x^2-1 & & \pmb{+} & \vline\hspace{-2.7pt}{0} & \pmb{-} & \vline\hspace{-2.7pt}{0} & \pmb{+} &\\\hline
e^{-x} & & \pmb{+} & \vline\hspace{-2.7pt}{\phantom 0} & \pmb{+} & \vline\hspace{-2.7pt}{\phantom 0} & \pmb{+} &\\\hline
(x^2-1)e^{-x} & & \pmb{+} & \vline\hspace{-2.7pt}{0} & \pmb{-} & \vline\hspace{-2.7pt}{0} & \pmb{+} &\\
\hline
\end{array}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/20.png)
Donc sur les intervalles![$]-\infty~;~-1[$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/21.png) et
et ![$]1~;~+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/22.png) ,
la courbe
,
la courbe 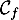 est au dessus de la courbe
est au dessus de la courbe 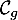 ,
et sur l'intervalle
,
et sur l'intervalle ![$]-1~;~1[$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/25.png) , la courbe
, la courbe 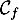 est en dessous
de la courbe
est en dessous
de la courbe 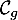 ,
,
- Les abscisses des points d'intersection de
-
- On a
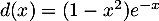 , soit
, soit 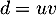 avec
avec 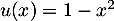 donc
donc 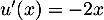 ,
et
,
et 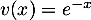 soit
soit 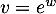 donc
donc 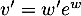 et donc
et donc
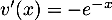 .
On a alors
.
On a alors  , soit
, soit
![\[\begin{array}{ll}d'(x)&=-2xe^{-x}+\lp1-x^2\rp\lp-e^{-x}\rp\\
&=e^{-x}\lp-2x-1+x^2\right)
\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/37.png)
- Dans la dérivée précédente, on a
 pour tout réel
pour tout réel 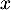 ,
et le trinôme du second degré a pour discriminant
,
et le trinôme du second degré a pour discriminant
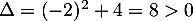 et admet donc deux racines
et admet donc deux racines
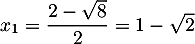 et
et 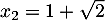 .
.
On a alors
![\[\renewcommand{\arraystretch}{1.5}
\def\esp{\hspace*{0cm}}
\begin{array}{|c | *{11}{c} |} \hline
x & -\infty & \esp & -1 & \esp & 1-\sqrt{2} & \esp & 1 & \esp & 1+\sqrt{2} & \esp & +\infty \\\hline
e^{-x} & & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \vline\hspace{-2.7pt}{\phantom 0} & + &\\\hline
x^2-2x-1& & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \vline\hspace{-2.7pt}{0} & - & \vline\hspace{-2.7pt}{\phantom 0} & - & \vline\hspace{-2.7pt}{0} & + &\\\hline
d'(x)& & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \vline\hspace{-2.7pt}{0} & - & \vline\hspace{-2.7pt}{\phantom 0} & - & \vline\hspace{-2.7pt}{0} & + &\\\hline
&&&&&&&&&&&\\
$d$&&&\psline[arrowsize=7pt]{->}(-.8,-.3)(1,.8)&&&
\psline[arrowsize=7pt]{->}(-.7,.8)(1.4,-.3)&&&&
\psline[arrowsize=7pt]{->}(-.8,-.3)(1,.8)&\\
&&&&&&&&&&&\\\hline
\end{array}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/43.png)
- Sur l'intervalle
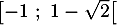 ,
, 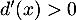 donc
donc  est strictement croissante.
est strictement croissante.
- Sur l'intervalle
![$\left ]1-\sqrt{2}~;~1\right ]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/47.png) ,
, 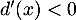 donc
donc  est strictement décroissante.
est strictement décroissante.
- Sur l'intervalle
- D'après la question précédente, la distance
 est maximale
pour
est maximale
pour  , et vaut alors
, et vaut alors
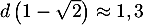
- On a
- On étudie la fonction
 .
.
La fonction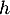 est dérivable, donc continue ssur
est dérivable, donc continue ssur  , avec
, avec
 donc, comme
donc, comme  ,
et donc
,
et donc  et la fonction
et la fonction  est
donc strictement décroissante sur
est
donc strictement décroissante sur  .
.
-
 ; comme
; comme 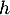 est strictement décroissante,
est strictement décroissante, 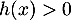 pour
pour 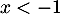 , donc
, donc 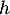 ne s'annule pas sur l'intervalle
ne s'annule pas sur l'intervalle ![$]-\infty~;~-1[$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/66.png) .
.
-
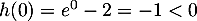 ; comme
; comme 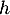 est strictement décroissante,
est strictement décroissante, 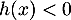 pour
pour 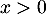 , donc
, donc 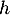 ne s'annule pas sur l'intervalle
ne s'annule pas sur l'intervalle ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/72.png) .
.
- Sur l'intervalle
![$[-1~;~0]$](/Generateur-Devoirs/TS/ChapExponentielle/ex15032021_c/73.png) , la fonction
, la fonction  est continue et strictement décroissante, et on sait que
est continue et strictement décroissante, et on sait que  et
et  ; donc d'après le corollaire du théorème des valeurs intermédiaires, ou théorème de la bijection,
l'équation
; donc d'après le corollaire du théorème des valeurs intermédiaires, ou théorème de la bijection,
l'équation  admet une solution unique.
admet une solution unique.
La droite et la courbe
et la courbe  ont donc un unique point d'intersection dont l'abscisse est comprise entre
ont donc un unique point d'intersection dont l'abscisse est comprise entre 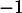 et
et 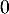 .
.
-
Cacher la correction
Exercice 8: Bac 2021: étude de fonction avec exponentielle
Partie 1
On donne ci-dessous, dans le plan rapporté à un repère orthonormé, la courbe représentant la fonction dérivée
À l'aide de cette courbe, conjecturer, en justifiant les réponses :
- Le sens de variation de la fonction
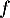 sur
sur  .
.
- La convexité de la fonction
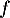 sur
sur  .
.
(4,4.5)
\psaxes[linewidth=1.25pt](0,0)(-2,-1.25)(4,4.5)
\psaxes[linewidth=1.25pt]{->}(0,0)(1,1)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=red]{-2}{4}{1 x add 2.71828 x exp div neg}
\rput(1,-1.5){Courbe repr\'esentant la \textbf{d\'eriv\'ee} $f'$ de la fonction $f$.}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021/8.png)
Partie 2
On admet que la fonction
On note
On admet que la fonction
- Montrer que, pour tout nombre réel
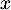 ,
,
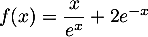 .
.
En déduire la limite de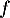 en
en 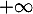 .
.
Justifier que la courbe admet une asymptote que l'on précisera.
admet une asymptote que l'on précisera.
On admet que .
.
-
- Montrer que, pour tout nombre réel
 ,
,  .
.
- Étudier les variations sur
 de la fonction
de la fonction 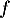 et dresser son tableau de variations.
et dresser son tableau de variations.
- Montrer que l'équation
 admet une unique solution
admet une unique solution 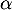 sur l'intervalle
sur l'intervalle ![$[-2~;~-1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021/32.png) dont on donnera une valeur approchée
à
dont on donnera une valeur approchée
à 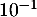 près.
près.
- Montrer que, pour tout nombre réel
- Déterminer, pour tout nombre réel
 , l'expression de
, l'expression de 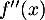 et étudier la convexité de la fonction
et étudier la convexité de la fonction  .
.
Que représente pour la courbe son point A d'abscisse
son point A d'abscisse  ?
?
Correction exercice 8
Baccalauréat général, spécialité mathématiques, Métropole 8 juin 2021
Partie 1
- D'après la courbe représentant la fonction dérivée
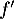 :
:
- la fonction
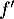 est positive sur
est positive sur ![$]-\infty~;~1[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/3.png) donc la fonction
donc la fonction 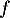 est croissante sur cet intervalle;
est croissante sur cet intervalle;
- la fonction
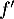 est négative sur
est négative sur ![$]1~;~+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/6.png) donc la fonction
donc la fonction 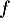 est décroissante sur cet intervalle.
est décroissante sur cet intervalle.
- la fonction
- D'après la courbe représentant la fonction dérivée
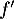 :
:
- la fonction
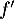 est décroissante sur
est décroissante sur ![$]-\infty~;~0[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/10.png) donc la fonction
donc la fonction 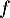 est concave sur cet intervalle;
est concave sur cet intervalle;
- la fonction
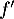 est croissante sur
est croissante sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/13.png) donc la fonction
donc la fonction 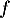 est convexe sur cet intervalle.
est convexe sur cet intervalle.
- la fonction
Partie 2
On admet que la fonction
- Pour tout nombre réel
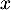 ,
,
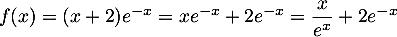 .
.
Par croissances comparées on a: donc
donc  .
.
De plus donc
donc  .
.
On en déduit que la courbe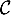 admet la droite d'équation
admet la droite d'équation  ,
c'est-à-dire l'axe des abscisses, comme asymptote horizontale en
,
c'est-à-dire l'axe des abscisses, comme asymptote horizontale en  .
.
-
-
 .
.
- Pour tout
 ,
, 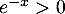 donc
donc 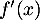 est du signe de
est du signe de  ;
donc
;
donc 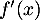 s'annule et change de signe en
s'annule et change de signe en 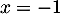 .
.
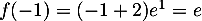 ;
on établit le tableau de variations de
;
on établit le tableau de variations de 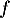 sur
sur 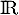 :
:
![\[{\renewcommand{\arraystretch}{1.5}
\psset{nodesep=1pt,arrowsize=5pt 3}
\def\esp{\hspace*{2.5cm}}
\def\hauteur{0pt}
\begin{array}{|c|l*4{c}|}
\hline
x & -\infty & \esp & -1 & \esp & +\infty \\
\hline
-x-1 & & + & \vline\hspace{-2.7pt}0 & - & \\
\hline
f'(x) & & + & \vline\hspace{-2.7pt}0 & - & \\
\hline
& & & \Rnode{max}{e} & & \rule{0pt}{\hauteur} \\
f(x) & & & & & \rule{0pt}{\hauteur} \\
& \Rnode{min1}{-\infty} & & & & \Rnode{min2}{0} \rule{0pt}{\hauteur}
\ncline{->}{min1}{max}
\ncline{->}{max}{min2}
\\
\hline
\end{array}}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/37.png)
- Sur l'intervalle
![$[-2~;~-1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/38.png) , la fonction
, la fonction  est strictement croissante
et continue car dérivable sur cetintervalle.
est strictement croissante
et continue car dérivable sur cetintervalle. 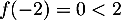 et
et  donc,
d'après le corollaire du théorème des valeurs intermédiaires
(ou théorème de la bijection),
l'équation
donc,
d'après le corollaire du théorème des valeurs intermédiaires
(ou théorème de la bijection),
l'équation  admet une solution unique sur l'intervalle
admet une solution unique sur l'intervalle ![$[-2~;~-1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/43.png) .
.
Avec la calculatrice, on trouve .
.
-
-
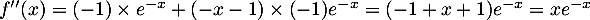
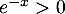 pour tout
pour tout 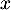 , donc
, donc 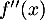 est du signe de
est du signe de 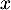 .
.
- Sur
![$]-\infty~;~0[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/50.png) ,
, 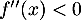 donc la fonction
donc la fonction 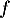 est concave.
est concave.
- Sur
![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex08062021_c/53.png) ,
, 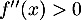 donc la fonction
donc la fonction 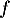 est convexe.
est convexe.
- En
 , la dérivée seconde s'annule et change de signe donc le point A d'abscisse 0 de
, la dérivée seconde s'annule et change de signe donc le point A d'abscisse 0 de 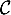 est le point d'inflexion de cette courbe.
est le point d'inflexion de cette courbe.
- Sur
Cacher la correction
Exercice 9: Bac 2019, Antille-Guyane - Fonction avec exponentielle, éléments graphiques, étude et primitive
Partie A
Soit
La courbe
La courbe
![\[\psset{xunit=0.675cm,yunit=4.8cm,comma=true}
\begin{pspicture}(-1,-0.05)(20,1,2)
\psaxes[linewidth=1.25pt,Dy=0.1]{->}(0,0)(0,0)(20,1.2)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{20}{1 1 2.71828 x 0.2 mul neg exp add div}
\psplot[plotpoints=2000,linewidth=1.25pt]{0}{14}{x 0.05 mul 0.5 add}
\psdots(10,1)\uput[ul](10,1){B}
\uput[u](17,0.95){\blue $\mathcal{C}_f$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019/10.png)
- Justifier que
 .
.
On obtient alors, pour tout réel ,
,
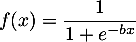 .
.
- On admet que la fonction
 est dérivable sur
est dérivable sur  et on note
et on note 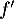 sa fonction
dérivée.
sa fonction
dérivée.
Vérifier que, pour tout réel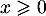
![\[f'(x)=\dfrac{be^{-bx}}{\lp1+e^{-bx}\rp^2}.\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019/18.png)
- En utilisant les données de l'énoncé, déterminer
 .
.
Partie B
La proportion d'individus qui possèdent un certain type d'équipement dans une population est modélisée par la fonction
Le réel
Le nombre
Ainsi, pour ce modèle,
- Quelle est, pour ce modèle, la proportion d'individus équipés au 1er janvier 2010? On en donnera une valeur arrondie au centième.
-
- Déterminer le sens de variation de la fonction
 sur
sur  .
.
- Calculer la limite de la fonction
 en
en  .
.
- Interpréter cette limite dans le contexte de l'exercice.
- Déterminer le sens de variation de la fonction
- On considère que, lorsque la proportion d'individus équipés dépasse 95 %, le marché est saturé. Déterminer, en expliquant la démarche, l'année au cours de laquelle cela se produit.
-
- Vérifier que, pour tout réel
 ,
,
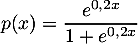 .
.
- En déduire une primitive
 de la fonction
de la fonction 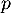 .
.
- La proportion moyenne d'individus équipés entre 2008 et 2010
est donnée par le nombre
 .
Déterminer une valeur arrondie au centième de
.
Déterminer une valeur arrondie au centième de  .
.
- Vérifier que, pour tout réel
Correction exercice 9
Partie A
-

- On a
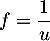 avec
avec 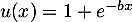 donc
donc 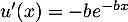
et alors , soit
, soit
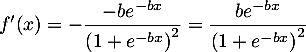
- La tangente à
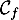 en
en  passe par
passe par
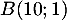 .
Le coefficient directeur de cette tangente est
donc
.
Le coefficient directeur de cette tangente est
donc
![\[m=\dfrac{1-0,5}{10-0}=\dfrac1{20}=0,05\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/10.png)
Par ailleurs, ce coefficient directeur est aussi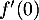 ,
et donc
,
et donc
![\[f'(0)=\dfrac{b}{\lp1+e^0\rp^2}=\dfrac{b}4=0,05
\iff b=0,2\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/12.png)
Partie B
- En 2010, on a
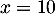 , et donc la proportion d'individus équipés
est
, et donc la proportion d'individus équipés
est 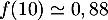 .
.
-
- Comme vu à la question 2, partie A,
on a, avec
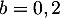 ,
,
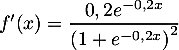 et donc, comme
et donc, comme  et
et
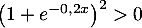 ,
la fonction
,
la fonction  est strictement croissante sur
est strictement croissante sur  donc aussi sur
donc aussi sur
 .
.
- En
 , on a
, on a
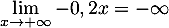 , donc par composition
, donc par composition
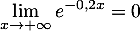 et donc, finalement
et donc, finalement
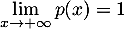 .
.
- Au bout d'un temps assez long, tout le monde va posséder ce type d'équipement.
- Comme vu à la question 2, partie A,
on a, avec
- On cherche
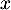 tel que
tel que
![\[\begin{array}{ll}p(x)>95\%=0,95
&\iff \dfrac{1}{1 + e^{-0,2x}}>0,95\\
&\iff 1 + e^{-0,2x}<\dfrac1{0,95}\\
&\iff e^{-0,2x}<\dfrac1{0,95}-1=\dfrac{0,05}{0,95}\\
&\iff -0,2x<\ln\lp\dfrac{0,05}{0,95}\rp\\
&\iff x>-\dfrac1{0,2}\ln\lp\dfrac{0,05}{0,95}\rp\simeq14,7
\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/27.png)
Cela se produit donc au cours de la 14ème année. -
-
![\[p(x) = \dfrac{1}{1 + e^{-0,2x}}
=\dfrac{e^{0,2x}}{e^{0,2x}}\tm\dfrac{1}{1 + e^{-0,2x}}
=\dfrac{e^{0,2x}}{1 + e^{0,2x}}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/28.png)
- Exprimer sous cette forme, on a donc
 de la forme
de la forme 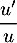 , et on trouve donc une primitive
, et on trouve donc une primitive
![\[P(x)=\dfrac1{0,2}\ln\lp1+e^{0,2x}\rp=5\ln\lp1+e^{0,2x}\rp\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/31.png)
- La proportion moyenne d'individus équipés entre 2008 et 2010
est alors
![\[m=\dfrac{P(10)-P(8)}2
=\dfrac12\left(
\dfrac1{0,2}\ln\lp1+e^{2}\right)
+
\dfrac1{0,2}\ln\lp1+e^{1,6}\rp\rp\simeq 0,86
\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/32.png)
-
Cacher la correction
Exercice 10: Bac 2017, Antilles-Guyane - Exponentielles et tangentes perpendiculaires
Soit 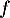 et
et 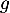 les fonctions définies sur
les fonctions définies sur  par
par
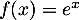 et
et 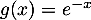 .
.
On note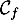 la courbe représentative de
la courbe représentative de 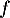 et
et 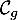 celle de
celle de 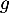 dans un repère orthonormé du plan.
dans un repère orthonormé du plan.
Pour tout réel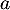 , on note
, on note  le point de
le point de 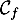 d'abscisse
d'abscisse 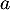 et
et 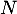 le point de
le point de 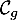 d'abscisse
d'abscisse  .
.
La tangente en à
à 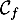 coupe l'axe des abscisses en
coupe l'axe des abscisses en 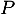 ,
la tangente en
,
la tangente en 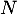 à
à 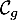 coupe l'axe des abscisses en
coupe l'axe des abscisses en  ,
,
D'après Bac Antilles Guyane 2017
Cacher la correction
On note
Pour tout réel
La tangente en
- Faire une figure représentant la situation.
Que vaut la longueur
 sur cette figure ?
sur cette figure ?
- Démontrer que la tangente en
 à
à  est perpendiculaire
à la tangente en
est perpendiculaire
à la tangente en 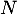 à
à 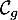 .
.
- Démontrer que, indépendamment de la valeur du réel
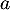 , on a
, on a
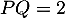 .
.
Correction exercice 10
D'après Bac Antilles Guyane 2017
-
{$\i$}}
\psplot[linewidth=1.6pt]{-5}{3}{2.718 x exp}
\psplot[linewidth=1.6pt]{-3}{5}{2.718 -1 x mul exp}
\psline[linestyle=dashed](.5,0)(!.5\space 2.718 .5 exp)
\rput(.5,-.2){$x$}
\rput(.65,.7){$N$}\rput(.65,1.6){$M$}
\psplot{-3}{3}{2.718 .5 exp x .5 add mul}
\psplot{-3}{3}{2.718 -.5 exp -1 mul x 1.5 sub mul}
\rput(-.45,-.2){$P$}
\rput(1.5,-.2){$Q$}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex-exp-tgt_c/1.png)
-
La tangente en
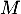 à
à 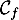 a pour équation
a pour équation
![\[\begin{array}{ll}y&=f'(a)(x-a)+f(a)=e^a(x-a)+e^a\\[.4em]
&=e^ax+e^a(1-a)\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex-exp-tgt_c/4.png)
Une équation cartésienne de cette droite est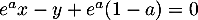 ,
et donc
,
et donc 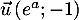 est un vecteur normal à cette droite.
est un vecteur normal à cette droite.
De même, la tangente en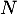 à
à 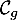 a pour équation
a pour équation
![\[\begin{array}{ll}y&=g'(a)(x-a)+g(a)=-e^{-a}(x-a)+e^{-a}\\[.4em]
&=-e^{-a}x+e^{-a}(1+a)\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex-exp-tgt_c/9.png)
Une équation cartésienne de cette droite est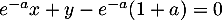 et donc
et donc
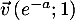 est un vecteur normal à cette droite.
est un vecteur normal à cette droite.
On a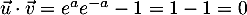 ,
ce qui montre que ces vecteurs sont orthogonaux, comme ces deux tangentes,
qui sont donc perpendiculaires.
,
ce qui montre que ces vecteurs sont orthogonaux, comme ces deux tangentes,
qui sont donc perpendiculaires.
- On détermine les abscisses des points
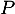 et
et 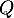 , qui sont à
l'intersection des deux tangentes et de l'axe des abscisses.
, qui sont à
l'intersection des deux tangentes et de l'axe des abscisses.
On a donc, pour le point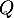 ,
,
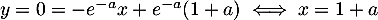 .
.
De même, pour le point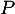 ,
,
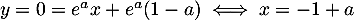 .
.
On en déduit donc que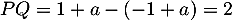 et ne dépend
donc pas de l'abscisse
et ne dépend
donc pas de l'abscisse 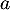 des points
des points  et
et  .
.
Cacher la correction
Exercice 11: Bac 2016, Amérique du nord - Volume d'un récupérateur d'eau
Un particulier veut faire fabriquer un récupérateur d'eau.
Ce récupérateur d'eau est une cuve qui doit respecter le cahier des
charges suivant:
Cette cuve est schématisée ci-contre.
![$$(-1.8,-0.5)(7,5)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\pspolygon(2,0)(2,1.8)(-1.3,2.5)(-1.3,0.7)
\rput(-3.3,0.7){\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}}
\psline(2.1,2.7)(5.4,2)
\psline(-1.3,2.5)(2.1,2.7)
\psline(2,1.8)(5.4,2)
\psline[linewidth=0.5pt](2,1.8)(2,3)\psline[linewidth=0.5pt](-1.3,2.5)(-1.3,3.7)
\psset{arrowsize=2pt 3}
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(2,3)(-1.3,3.7)
\psline[linewidth=0.5pt](2,1.8)(1.2,1.75)\psline[linewidth=0.5pt](2,0)(1.2,-0.05)
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(1.2,1.75)(1.2,-0.05)
\uput[l](1.2,0.85){2 m}\uput[u](1.35,3.35){5 m}
$$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/1.png)
La partie incurvée est modélisée par la courbe de la
fonction
de la
fonction 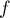 sur l'intervalle
sur l'intervalle ![$[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/4.png) définie par:
définie par:
![\[f(x)=x\ln \lp\dfrac{x}{2}\rp-x+2.\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/5.png)
La courbe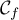 est représentée ci-dessous dans un repère
orthonormé d'unité 1m et constitue une vue de profil de la cuve.
est représentée ci-dessous dans un repère
orthonormé d'unité 1m et constitue une vue de profil de la cuve.
On considère les points ,
,  et
et 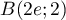 .
.
(-0.2,-0.25)(6,2.5)
\psaxes[linewidth=1.25pt](0,0)(0,0)(6,2.5)
\uput[u](2.8,0.2){$\mathcal{C}_f$}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\psframe[fillstyle=solid,fillcolor=lightgray](2,2)
\psdots(2,2)(5.437,2)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psplot[plotpoints=4000]{3}{5.8}{x 2 add 5.437 sub}
\uput[u](2,2){$A$}
\uput[u](5.437,2){$B$}
\uput[ul](5.75,2.2){$\mathcal{T}$}
\uput[dl](2,0){$I$}
\uput[dr](3.437,0){$D$}
\rput(1,1){Terrain}
\rput(3.2,1.2){Cuve}
\rput(4.7,0.5){Terrain}
\psline[linestyle=dotted,linewidth=1.5pt](2,2)(5.437,2)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/10.png)
Partie A L'objectif de cette partie est d'évaluer le volume de la cuve.
Partie B Pour tout réel compris
entre
compris
entre  et
et  , on note
, on note 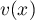 le volume d'eau, exprimé en m
le volume d'eau, exprimé en m ,
se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est
égale à
,
se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est
égale à 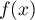 .
.
On admet que, pour tout réel de l'intervalle [2 ; 2e],
de l'intervalle [2 ; 2e],
![\[v(x) = 5\left[\dfrac{x^2}{2}\ln \left( \dfrac{x}{2}\right) - 2x\ln\left( \dfrac{x}{2}\right) - \dfrac{x^2}{4} + 2x - 3\right].\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/49.png)
{\n}}
}
\pspolygon[fillstyle=solid,fillcolor=gray](2,0.1)(2,1.5)(0.35,2.3)(0.35,0.9)
\pspolygon[fillstyle=solid,fillcolor=gray](2,1.5)(0.35,2.3)(3.37,2.47)(5.08,1.7)
\pscustom[fillstyle=solid,fillcolor=gray]{
\pscurve(2,0.1)(3,0.316)(4,0.87)(5.08,1.75)
\psline(5.08,1.75)(2,1.5)
}
\pspolygon(5.437,2.1)(2,1.85)(0.35,2.7)(3.787,2.95)
\psline(2,1.85)(2,1.5)
\psline(0.35,2.7)(0.35,2.3)
\pscurve(0.35,0.9)(1.35,1.16)(2.35,1.72)(3.35,2.5)(3.787,2.95)
\psline[linestyle=dotted,linewidth=1.5pt](5.08,0.2)(5.08,1.75)(0,1.37)
\uput[d](5.2,0.3){$x$}
\uput[l](0,1.37){$f(x)$}
\multido{\n=0+1}{4}{\uput[l](0,\n){\n}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/50.png)
Bac S - Amérique du nord, juin 2016 - 6 points
Partie A
Partie B
Cacher la correction
- elle doit être située à deux mètres de sa maison;
- la profondeur maximale doit être de deux mètres;
- elle doit mesurer cinq mètres de long;
- elle doit épouser la pente naturelle du terrain.
Cette cuve est schématisée ci-contre.
![$$(-1.8,-0.5)(7,5)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\pspolygon(2,0)(2,1.8)(-1.3,2.5)(-1.3,0.7)
\rput(-3.3,0.7){\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}}
\psline(2.1,2.7)(5.4,2)
\psline(-1.3,2.5)(2.1,2.7)
\psline(2,1.8)(5.4,2)
\psline[linewidth=0.5pt](2,1.8)(2,3)\psline[linewidth=0.5pt](-1.3,2.5)(-1.3,3.7)
\psset{arrowsize=2pt 3}
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(2,3)(-1.3,3.7)
\psline[linewidth=0.5pt](2,1.8)(1.2,1.75)\psline[linewidth=0.5pt](2,0)(1.2,-0.05)
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(1.2,1.75)(1.2,-0.05)
\uput[l](1.2,0.85){2 m}\uput[u](1.35,3.35){5 m}
$$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/1.png)
La partie incurvée est modélisée par la courbe
La courbe
On considère les points
(-0.2,-0.25)(6,2.5)
\psaxes[linewidth=1.25pt](0,0)(0,0)(6,2.5)
\uput[u](2.8,0.2){$\mathcal{C}_f$}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\psframe[fillstyle=solid,fillcolor=lightgray](2,2)
\psdots(2,2)(5.437,2)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psplot[plotpoints=4000]{3}{5.8}{x 2 add 5.437 sub}
\uput[u](2,2){$A$}
\uput[u](5.437,2){$B$}
\uput[ul](5.75,2.2){$\mathcal{T}$}
\uput[dl](2,0){$I$}
\uput[dr](3.437,0){$D$}
\rput(1,1){Terrain}
\rput(3.2,1.2){Cuve}
\rput(4.7,0.5){Terrain}
\psline[linestyle=dotted,linewidth=1.5pt](2,2)(5.437,2)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/10.png)
Partie A L'objectif de cette partie est d'évaluer le volume de la cuve.
- Justifier que les points
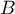 et
et 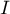 appartiennent à la courbe
appartiennent à la courbe
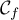 et que l'axe des abscisses est tangent à la courbe
et que l'axe des abscisses est tangent à la courbe
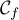 au point
au point  .
.
- On note
 la tangente à la courbe
la tangente à la courbe  au
point
au
point  , et
, et  le point d'intersection de la droite
le point d'intersection de la droite  avec l'axe des abscisses.
avec l'axe des abscisses.
- Déterminer une équation de la droite
 et en
déduire les coordonnées de
et en
déduire les coordonnées de  .
.
- On appelle
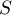 l'aire du domaine délimité par la courbe
l'aire du domaine délimité par la courbe
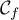 , les droites d'équations
, les droites d'équations  ,
,  et
et  .
.
 peut être encadrée par l'aire du triangle
peut être encadrée par l'aire du triangle  et celle du
trapèze
et celle du
trapèze  .
.
Quel encadrement du volume de la cuve peut-on en déduire ?
- Déterminer une équation de la droite
-
- Montrer que, sur l'intervalle
![$[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/31.png) ,
la fonction
,
la fonction  définie par
définie par
![\[G(x)=\dfrac{x^2}{2}\ln \lp\dfrac{x}{2}\rp-\dfrac{x^2}{4}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/33.png)
est une primitive de la fonction définie par
définie par
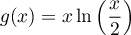 .
.
- En déduire une primitive
 de la fonction
de la fonction  sur
l'intervalle
sur
l'intervalle ![$[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/38.png) .
.
- Déterminer la valeur exacte de l'aire
 et en déduire une
valeur approchée du volume
et en déduire une
valeur approchée du volume 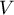 de la cuve au
de la cuve au  près.
près.
- Montrer que, sur l'intervalle
Partie B Pour tout réel
On admet que, pour tout réel
{\n}}
}
\pspolygon[fillstyle=solid,fillcolor=gray](2,0.1)(2,1.5)(0.35,2.3)(0.35,0.9)
\pspolygon[fillstyle=solid,fillcolor=gray](2,1.5)(0.35,2.3)(3.37,2.47)(5.08,1.7)
\pscustom[fillstyle=solid,fillcolor=gray]{
\pscurve(2,0.1)(3,0.316)(4,0.87)(5.08,1.75)
\psline(5.08,1.75)(2,1.5)
}
\pspolygon(5.437,2.1)(2,1.85)(0.35,2.7)(3.787,2.95)
\psline(2,1.85)(2,1.5)
\psline(0.35,2.7)(0.35,2.3)
\pscurve(0.35,0.9)(1.35,1.16)(2.35,1.72)(3.35,2.5)(3.787,2.95)
\psline[linestyle=dotted,linewidth=1.5pt](5.08,0.2)(5.08,1.75)(0,1.37)
\uput[d](5.2,0.3){$x$}
\uput[l](0,1.37){$f(x)$}
\multido{\n=0+1}{4}{\uput[l](0,\n){\n}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/50.png)
- Quel volume d'eau, au m
 près, y a-t-il dans la cuve lorsque
la hauteur d'eau dans la cuve est de un mètre ?
près, y a-t-il dans la cuve lorsque
la hauteur d'eau dans la cuve est de un mètre ?
- On rappelle que
 est le volume total de la cuve,
est le volume total de la cuve, 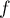 est la
fonction définie en début d'exercice et
est la
fonction définie en début d'exercice et 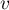 la fonction définie dans
la partie B.
la fonction définie dans
la partie B.
On considère l'algorithme ci-dessous.
Interpréter le résultat que cet algorithme permet d'afficher.
Variables: a est un réel
b est un réelTraitement: a prend la valeur 2
b prend la valeur 2e
Tant que v(b)-v(a)>10-3 faire:
c prend la valeur (a+b)/2Fin Tant que
Si v(c)<V/2, alors:
a prend la valeur cSinonb prend la valeur cFin SiSortie: Afficher f(c)
Correction exercice 11
Bac S - Amérique du nord, juin 2016 - 6 points
Partie A
- On a
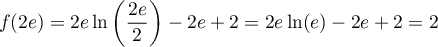 ,
car
,
car 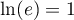 , et donc
, et donc 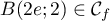 .
.
De même,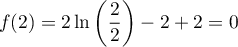 ,
car
,
car 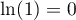 , et donc
, et donc  .
.
De plus, en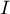 le coefficient directeur de la tangente à
le coefficient directeur de la tangente à
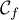 est
est 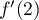 .
.
On a, pour tout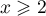 ,
,
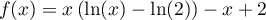 ,
soit
,
soit 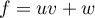 ,
avec
,
avec 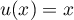 , donc
, donc 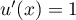 ,
,
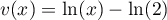 , donc
, donc 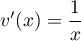 ,
et
,
et 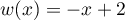 , donc
, donc 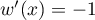 .
.
On a alors,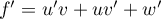 ,
soit
,
soit
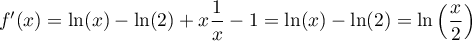 .
.
Ainsi, la tangente à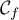 en
en  a pour coefficient
directeur
a pour coefficient
directeur 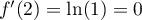 et passe par
et passe par  : c'est l'axe des
abscisses.
: c'est l'axe des
abscisses.
-
- Une équation de
 est:
est:
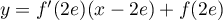 ,
avec
,
avec 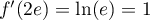 et
et 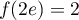 ,
d'où
,
d'où
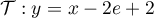 .
.
On a alors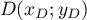 avec
avec 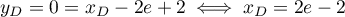 .
Ainsi,
.
Ainsi, 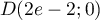 .
.
- L'aire de
 , trangle rectangle en
, trangle rectangle en  , est
, est
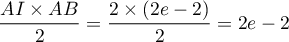
et l'aire du trapèze est
est
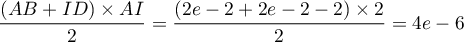 .
.
Ainsi le volume de la cuve est tel que
de la cuve est tel que
![\[5e\leqslant V\leqslant 5(4e-6)\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/39.png)
soit approximativement
![\[17,18\leqslant V\leqslant 24,37\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/40.png)
- Une équation de
-
- On a
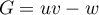 avec
avec 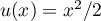 , donc
, donc 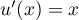 ,
,
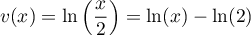 , donc
, donc 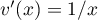 ,
et
,
et 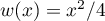 , donc
, donc 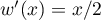 .
.
On a alors,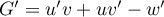 ,
soit
,
soit
![\[\begin{array}{ll}
G'(x)&=x\ln\lp\dfrac{x}2\rp+\dfrac{x^2}{2}\tm\dfrac1x-\dfrac{x}{2}\\[1em]
&=x\ln\lp\dfrac{x}{2}\rp+\dfrac{x}{2}-\dfrac{x}{2}\\[.8em]
&=g(x)\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/49.png)
ce qui montre que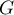 est bien une primitive de
est bien une primitive de 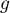 .
.
- On en déduit qu'une primitive de
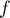 définie par
définie par
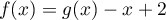 est donnée par
est donnée par
![\[F(x)=G(x)-\dfrac12x^2+2x\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/54.png)
- On peut alors calculer l'intégrale:
![\[\begin{array}{ll}
S&\dsp=\int_2^{2e}\Bigl(2-f(x)\Bigr)dx\\[1em]
&=\Bigl[ 2x-F(x)\Bigr]_2^{2e}\\[1em]
&=\Bigl[ -G(x)+\dfrac12x^2\Bigr]_2^{2e}\\[1em]
&=-G(2e)+\dfrac12(2e)^2-\Bigl(-G(2)+\dfrac122^2\Bigr)\\[.7em]
&=G(2)-G(2e)+2e^2-2
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/55.png)
avec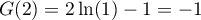 ,
et
,
et 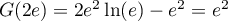 ,
donc
,
donc
![\[S=-1-e^2+2e^2-2=e^2-3\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/58.png)
et on en déduit le volume de la cuve: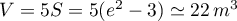 .
.
- On a
Partie B
- Le volume est
 avec
avec 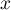 tel que
tel que 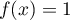 .
On cherche donc à résoudre l'équation
.
On cherche donc à résoudre l'équation 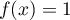 ,
avec
,
avec 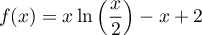 .
.
On ne sait pas résoudre excactement cette équation. On peut par contre le faire de manière approchée, en utilisant le théorème des valeurs intermédiaires.
On sait que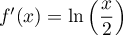 , d'après A.1.
et donc, comme
, d'après A.1.
et donc, comme  est strictement croissante sur
est strictement croissante sur  ,
que pour tout
,
que pour tout ![$x\in[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/68.png) ,
,
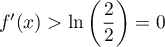 .
.
Ainsi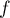 est strictement croissante sur
est strictement croissante sur ![$[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/71.png) , avec de plus
, avec de plus
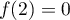 et
et 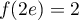 .
On en déduit, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
qu'il existe une unique solution
.
On en déduit, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
qu'il existe une unique solution ![$\alpha\in[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/74.png) à l'équation
à l'équation
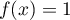 .
.
Avec la calculatrice (à l'aide d'un tableau de valeurs, ou par dichotomie par exemple), on trouve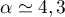 , et alors
le volume est de
, et alors
le volume est de 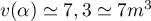 .
.
- Cet algorithme est un algorithme de recherche par dichotomie.
Il permet de chercher les valeurs d'un encadrement![$[a;b]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/78.png) pour lequel
la hauteur
pour lequel
la hauteur 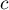 correspond à la moitié de la cuve.
correspond à la moitié de la cuve.
Cet encadrement permet d'avoir un résultat précis à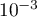 près.
près.
Cacher la correction
Exercice 12: Bac 2015, Nouvelle Calédonie - Etude de fonctions avec un paramètre et une exponentielle
Le plan est rapporté à un repère orthogonal 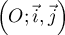 .
.
Soit un nombre réel strictement positif.
un nombre réel strictement positif.
On note la droite d'équation
la droite d'équation  et
et  la courbe représentative de la fonction exponentielle dans le repère orthogonal
la courbe représentative de la fonction exponentielle dans le repère orthogonal  .
.
Le but de cet exercice est de déterminer le nombre de points d'intersection de et
et  suivant les valeurs de
suivant les valeurs de 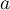 .
.
Pour cela. on considère la fonction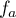 définie pour tout nombre réel
définie pour tout nombre réel 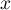 par
par
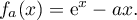
On admet pour tout réel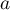 que la fonction
que la fonction 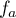 est dérivable sur l'ensemble
est dérivable sur l'ensemble  des nombres réels.
des nombres réels.
![\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-0.4)(2,5)
\psaxes[linewidth=1.25pt]{->}(0,0)(-1,-0.4)(2,5)
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=green]{-1}{2}{x 2 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=red]{-1}{2}{x 2.71828 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=cyan]{-1}{2}{x 3 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=blue]{-1}{2}{2.71828 x exp }
\rput{45}(1.8,3.4){\green $y = 2x$}
\rput{53}(1.8,4.6){\red $y = \text{e}x$}
\rput{57}(1,3.2){\cyan $y = 3x$}
\rput(-0.5,0.75){\blue $\Gamma$}
\uput[ul](0,0){O}
\end{pspicture*}](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/71.png)
Cacher la correction
Soit
On note
Le but de cet exercice est de déterminer le nombre de points d'intersection de
Pour cela. on considère la fonction
On admet pour tout réel
- Étude du cas particulier
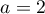 La fonction
La fonction 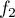 est donc définie pour tout
est donc définie pour tout 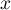 réel par
réel par
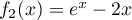 .
.
- Étudier les variations de la fonction
 sur
sur 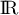 et dresser
son tableau de variations sur
et dresser
son tableau de variations sur  (on ne demande pas de
déterminer les limites aux bornes de l'ensemble de définition.
(on ne demande pas de
déterminer les limites aux bornes de l'ensemble de définition.
- En déduire que
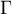 et
et 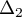 n'ont pas de point
d'intersection.
n'ont pas de point
d'intersection.
- Étudier les variations de la fonction
- Étude du cas général où
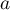 est un réel strictement positif
est un réel strictement positif
- Déterminer les limites de la fonction
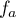 en
en  et en
et en
 .
.
- Étudier les variations de la fonction
 sur
sur  . Montrer
alors que le minimum sur
. Montrer
alors que le minimum sur  de la fonction
de la fonction  est
est
 .
.
- Étudier le signe de
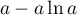 suivant les valeurs du
nombre réel strictement positif
suivant les valeurs du
nombre réel strictement positif 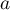 .
.
- Déterminer selon les valeurs du réel
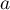 le nombre de points
communs à
le nombre de points
communs à  et
et  .
.
- Déterminer les limites de la fonction
Correction exercice 12
-
- D'après l'énoncé la fonction
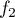 est dérivable sur
est dérivable sur 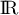 .
.
On a .
Or
.
Or 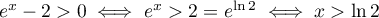 car la fonction
exponentielle est croissante.
On a donc le tableau de variations suivant :
car la fonction
exponentielle est croissante.
On a donc le tableau de variations suivant :
{$x$}\uput[u](1.5,2.4){$- \infty$}\uput[u](4,2.4){$\ln 2$}\uput[u](6.5,2.4){$+ \infty$}
\rput(0.5,2.25){$f'(x)$}\rput(2.5,2.25){$-$} \rput(4,2.25){$0$} \rput(5.5,2.25){$+$}
\rput(0.5,1){$f$}\uput[u](4,0){$2 - 2\ln 2$}
\psline{->}(1.5,1.5)(3.5,0.5)\psline{->}(4.5,0.5)(6.5,1.5)
\end{pspicture}](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/5.png)
- Comme
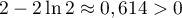 , on en déduit que la fonction est
strictement positive sur
, on en déduit que la fonction est
strictement positive sur  , soit
, soit
 .
.
Ainsi, la courbe représentative de la fonction
exponentielle est toujours strictement au dessus de la droite
représentative de la fonction
exponentielle est toujours strictement au dessus de la droite  .
.
En particulier, et
et 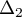 n'ont pas de point commun.
n'ont pas de point commun.
- D'après l'énoncé la fonction
-
-
 En plus l'infini :
En plus l'infini :
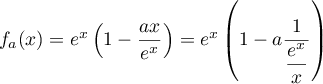 .
.
On sait que, par croissances comparées,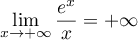 donc
donc
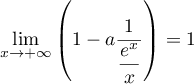 et donc,
comme
et donc,
comme 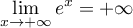 ,
par produit des limites
,
par produit des limites 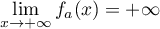 .
.
 En moins l'infini :
En moins l'infini :
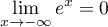 et
et 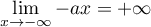 car
car 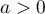 .
Donc, par addtion des limites,
.
Donc, par addtion des limites,  .
.
- D'après l'énoncé,
 est dérivable sur
est dérivable sur  , et on a
, et on a
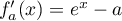 .
.
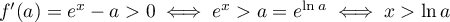 ,
car
,
car  et la fonction exponentielle est strictement croissante.
On a donc le même tableau de variations que pour
et la fonction exponentielle est strictement croissante.
On a donc le même tableau de variations que pour  en
remplaçant 2 par
en
remplaçant 2 par  .
En particulier, la fonction
.
En particulier, la fonction  admet donc un minimum en
admet donc un minimum en 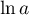 qui est
qui est  .
.
-
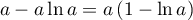 avec
avec 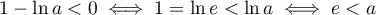 , par croissance de la
fonction logarithme; ainsi:
, par croissance de la
fonction logarithme; ainsi:
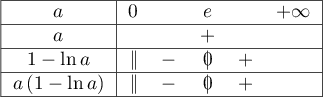
- D'après le tableau de signes précédent qui donne le signe du
minimum de
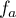 ,
,
 si
si 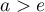 , alors
, alors 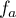 est strictement positive, et donc,
comme en 1),
est strictement positive, et donc,
comme en 1),  et
et 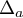 n'ont aucun point
d'intersection.
n'ont aucun point
d'intersection.
 si
si 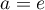 , alors
, alors  , et pour tout
, et pour tout 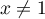
 .
.
 et
et  se coupent une unique fois
(
se coupent une unique fois
( est tangente à
est tangente à 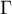 au point
au point 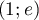 ).
).
 si
si 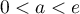 , le minimum de
, le minimum de  est négatif,
est négatif,
{$x$}\uput[u](1.5,2.4){$- \infty$}\uput[u](4,2.4){$\ln a$}\uput[u](6.5,2.4){$+ \infty$}
\uput[u](1.5,1.4){$+\infty$}\uput[u](6.5,1.4){$+\infty$}
\rput(0.5,2.25){$f'(x)$}\rput(2.5,2.25){$-$} \rput(4,2.25){$0$} \rput(5.5,2.25){$+$}
\rput(0.5,1){$f$}\uput[u](4,0){$a - 2\ln a$}
\psline{->}(1.5,1.5)(3.5,0.5)\psline{->}(4.5,0.5)(6.5,1.5)
\end{pspicture}](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/56.png)
Sur l'intervalle![$]-\infty~;~\ln a[](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/57.png) ,
la fonction
,
la fonction 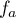 est continue (car dérivable),
strictement décroissante, avec
est continue (car dérivable),
strictement décroissante, avec 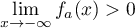 et
et
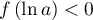 . Ainsi, d'après le théorème de la bijection (ou
corollaire du théorème des valeurs intérmédiaires),
il existe un unique
. Ainsi, d'après le théorème de la bijection (ou
corollaire du théorème des valeurs intérmédiaires),
il existe un unique ![$\alpha\in]-\infty;\ln a[](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/61.png) tel que
tel que
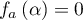
Le même raisonnement est aussi valable sur :
il existe un unique
:
il existe un unique ![$\beta\in]\ln a;+\infty[](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/64.png) tel que
tel que
 .
.
Ainsi, si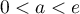 ,
,  et
et  ont deux points
d'intersections distincts (les points de coordonnées
ont deux points
d'intersections distincts (les points de coordonnées
 et
et 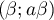 ).
).
-
![\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-0.4)(2,5)
\psaxes[linewidth=1.25pt]{->}(0,0)(-1,-0.4)(2,5)
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=green]{-1}{2}{x 2 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=red]{-1}{2}{x 2.71828 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=cyan]{-1}{2}{x 3 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=blue]{-1}{2}{2.71828 x exp }
\rput{45}(1.8,3.4){\green $y = 2x$}
\rput{53}(1.8,4.6){\red $y = \text{e}x$}
\rput{57}(1,3.2){\cyan $y = 3x$}
\rput(-0.5,0.75){\blue $\Gamma$}
\uput[ul](0,0){O}
\end{pspicture*}](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/71.png)
Cacher la correction
Exercice 13: Bac 2014, Antilles-Guyane - Etude de fonctions, limites, TVI, tangente, intégrale
On considère la fonction  définie et dérivable sur l'ensemble
définie et dérivable sur l'ensemble  des nombres réels par
des nombres réels par

On note sa courbe représentative.
sa courbe représentative.
Partie A
Partie B
(Bac S, Antilles-Guyane, juin 2014)
Partie A
Partie B
Cacher la correction
On note
- Soit
 la fonction définie et dérivable sur l'ensemble
la fonction définie et dérivable sur l'ensemble  par
par  .
Dresser, en le justifiant, le tableau donnant les variations de la
fonction
.
Dresser, en le justifiant, le tableau donnant les variations de la
fonction  sur
sur  (les limites de
(les limites de  aux bornes de son ensemble
de définition ne sont pas attendues).
En déduire le signe de
aux bornes de son ensemble
de définition ne sont pas attendues).
En déduire le signe de  .
.
- Déterminer la limite de
 en
en  puis la limite de
puis la limite de  en
en  .
.
- On appelle
 la dérivée de la fonction
la dérivée de la fonction  sur
sur  .
.
Démontrer que, pour tout réel ,
,
 .
.
- En déduire le tableau de variation de la fonction
 sur
sur  .
.
- Démontrer que l'équation
 admet une unique solution
réelle
admet une unique solution
réelle  sur
sur  .
Démontrer que
.
Démontrer que  .
.
-
- Démontrer que la droite
 d'équation
d'équation  est
tangente à la courbe
est
tangente à la courbe  au point d'abscisse
au point d'abscisse  .
.
- Étudier la position relative de la courbe
 et de
la droite
et de
la droite  .
.
- Démontrer que la droite
Partie B
- Soit
 la fonction définie et dérivable sur
la fonction définie et dérivable sur  par
par
 .
.
Démontrer que est une primitive sur
est une primitive sur  de la fonction
de la fonction  définie par
définie par  .
.
- On note
 le domaine délimité par la courbe
le domaine délimité par la courbe
 , la droite
, la droite  et les droites d'équation
et les droites d'équation
 et
et  .
Calculer, en unité d'aire, l'aire du domaine
.
Calculer, en unité d'aire, l'aire du domaine  .
.
Correction exercice 13
(Bac S, Antilles-Guyane, juin 2014)
Partie A
- Pour tout réel
 ,
,  .
On a alors
.
On a alors  , et donc,
, et donc,

On déduit du tableau précédent que, pour tout réel ,
,  .
.
- En
 .
.
 et
et  donc, par somme:
donc, par somme:  .
.
En .
.
 et, par croissances comparées
et, par croissances comparées  , donc, par somme
, donc, par somme  .
.
- Pour tout réel
 , on a:
, on a:

- On a vu plus haut que, pour tout réel
 ,
,  , et comme
par ailleurs
, et comme
par ailleurs  , on en déduit que
, on en déduit que  .
.
On obtient alors le tableau de variations suivant:

- La fonction
 est continue sur
est continue sur  ,
strictement croissante. D'après un corollaire du théorème des
valeurs intermédiaires (théorème de la bijection),
l'intervalle
,
strictement croissante. D'après un corollaire du théorème des
valeurs intermédiaires (théorème de la bijection),
l'intervalle  a
pour image
a
pour image  , ce dernier intervalle
contenant 0, on en déduit que l'équation
, ce dernier intervalle
contenant 0, on en déduit que l'équation  possède dans
possède dans
 une solution
une solution  unique.
unique.
Par ailleurs, et
et  , donc:
, donc:  .
.
-
- La tangente
 a pour équation réduite:
a pour équation réduite:

- Pour tout réel
 ,
,
 ,
,
et donc,

On en déduit que est située en dessous de
est située en dessous de  .
.
- La tangente
Partie B
- Pour tout réel
 ,
,
 ,
,
et la fonction est donc une primitive de
est donc une primitive de  sur
sur  .
.
- Sur
 ,
,  est en dessous de
est en dessous de  , l'aire
, l'aire  du domaine
du domaine  est donc:
est donc:

Cacher la correction
Exercice 14: Bac 2011, Amérique du nord - Fonctions avec exponentielle, position relative courbe/droite, puis suite récurrente
Partie A
On considère la fonction définie sur
définie sur  par
par
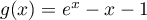 .
.
Partie B
On considère la fonction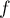 définie sur
définie sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/11.png) par
par
 .
.
La courbe représentative de la fonction
représentative de la fonction  dans le plan muni
d'un repère orthonormal est donnée en annexe.
Cette annexe sera complétée et remise avec la copie à la fin de
l'épreuve.
dans le plan muni
d'un repère orthonormal est donnée en annexe.
Cette annexe sera complétée et remise avec la copie à la fin de
l'épreuve.
On admet que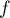 est strictement croissante sur
est strictement croissante sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/16.png) .
.
Partie C
On considère la suite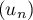 définie par:
définie par:
![$\la\begin{array}{ll} u_0=\dfrac12 \\[0.3cm] \text{pour tout entier naturel } n, u_{n+1}=f\left( u_n\rp\enar\right.](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/35.png) .
.
Annexe
Cette page sera complétée et remise avec la copie à la fin de l'épreuve.
![\psset{unit=5cm,arrowsize=7pt}
\fbox{\begin{pspicture}(-.2,-.2)(1.5,1.5)
\psline[linewidth=1.6pt]{->}(-.2,0)(1.5,0)
\psline[linewidth=1.6pt]{->}(0,-.2)(0,1.5)
\psplot{0}{1}{2.718 x exp 1 sub 2.718 x exp x sub div}
\newcommand{\f}[1]{#1 10 div}
\multido{\i=-2+1}{18}{
\psline[linewidth=.8pt,linestyle=dotted](!\f{\i}\space-.2)(!\f{\i}\space1.5)
\psline[linewidth=.8pt,linestyle=dotted](!-.2\space\f{\i})(!1.5\space\f{\i})
}
\rput(-.05,-.05){$O$}
\psline(1,-.02)(1,.02)\rput(1,-.08){$1$}
\psline(-.02,1)(.02,1)\rput(-.08,1){$1$}
\rput(.9,1.05){$(C)$}
\end{pspicture}}](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/39.png)
Partie A On considère la fonction définie sur
définie sur  par
par
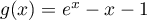 .
.
Partie B
Partie C
Cacher la correction
On considère la fonction
- Etudier les variations de la fonction
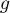 .
.
- Déterminer le signe de
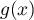 suivant les valeurs de
suivant les valeurs de  .
.
- En déduire que pour tout
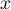 de
de  ,
, 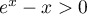 .
.
Partie B
On considère la fonction
La courbe
On admet que
- Montrer que pour tout
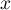 de
de ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/18.png) ,
, ![$f(x)\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/19.png) .
.
- Soit
 la droite d'équation
la droite d'équation 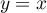 .
.
- Montrer que pour tout
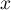 de
de ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/23.png) ,
, 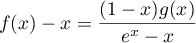 .
.
- Etudier la position relative de la droite
 et de la
courbe
et de la
courbe  sur
sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/27.png) .
.
- Montrer que pour tout
-
- Déterminer une primitive de
 sur
sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/29.png) .
.
- Calculer l'aire, en unité d'aire, du domaine du plan délimité
par la courbe
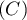 , la droite
, la droite  et les droites d'équations
et les droites d'équations
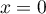 et
et  .
.
- Déterminer une primitive de
Partie C
On considère la suite
![$\la\begin{array}{ll} u_0=\dfrac12 \\[0.3cm] \text{pour tout entier naturel } n, u_{n+1}=f\left( u_n\rp\enar\right.](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/35.png) .
.
- Construire sur l'axe des abscisses les quatre premiers termes de la suite en laissant apparents les traits de construction.
- Montrer que pour tout entier
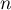 ,
,
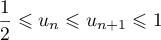 .
.
- En déduire que la suite
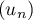 est convergente et
déterminer sa limite.
est convergente et
déterminer sa limite.
Annexe
Cette page sera complétée et remise avec la copie à la fin de l'épreuve.
![\psset{unit=5cm,arrowsize=7pt}
\fbox{\begin{pspicture}(-.2,-.2)(1.5,1.5)
\psline[linewidth=1.6pt]{->}(-.2,0)(1.5,0)
\psline[linewidth=1.6pt]{->}(0,-.2)(0,1.5)
\psplot{0}{1}{2.718 x exp 1 sub 2.718 x exp x sub div}
\newcommand{\f}[1]{#1 10 div}
\multido{\i=-2+1}{18}{
\psline[linewidth=.8pt,linestyle=dotted](!\f{\i}\space-.2)(!\f{\i}\space1.5)
\psline[linewidth=.8pt,linestyle=dotted](!-.2\space\f{\i})(!1.5\space\f{\i})
}
\rput(-.05,-.05){$O$}
\psline(1,-.02)(1,.02)\rput(1,-.08){$1$}
\psline(-.02,1)(.02,1)\rput(-.08,1){$1$}
\rput(.9,1.05){$(C)$}
\end{pspicture}}](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau/39.png)
Correction exercice 14
Partie A On considère la fonction
-
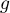 est la somme de la fonction exponentielle et d'une fonction
affine et est donc dérivable sur
est la somme de la fonction exponentielle et d'une fonction
affine et est donc dérivable sur  , donc sur
, donc sur 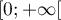 ,
avec,
,
avec, 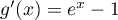 .
.
De plus, la fonction exponentielle est strictement croissante sur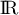 , lorsque
, lorsque ![$x\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/9.png) , on a
, on a 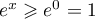 , et
donc
, et
donc  .
.
On a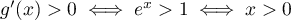 , car
Ainsi, on a le tableau de variation:
, car
Ainsi, on a le tableau de variation:
![\begin{tabular}{|c|cccc|}\hline
$x$ & $0$ &\hspace*{1cm}& &$+\infty$ \\\hline
$g'(x)$ &$0$& $+$ &&\\\hline
&&&&\\
$g$&&\psline[arrowsize=6pt]{->}(-.6,-.2)(1,.4)&&\\
&$0$&&&\\\hline
\end{tabular}](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/13.png)
- Comme
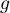 est strictement croissante sur
est strictement croissante sur 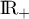 et que
et que 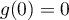 ,
on en déduit que pour tout
,
on en déduit que pour tout 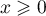 ,
,
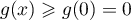 .
.
- On a donc pour tout
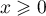 ,
,
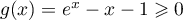 ,
et ainsi,
,
et ainsi,  .
.
Partie B
- Comme
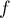 est strictement croissante sur
est strictement croissante sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/23.png) ,
on a
,
on a ![$x\in[0;1]\iff 0\leqslant x\leqslant 1\iff f(0)\leqslant f(x)\leqslant f(1)](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/24.png) .
.
Or et
et  ,
et on a donc bien ainsi
,
et on a donc bien ainsi ![$0\leqslant f(x)\leqslant 1 \iff f(x)\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/27.png) .
.
- Soit
 la droite d'équation
la droite d'équation 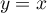 .
.
- Pour tout
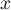 de
de ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/31.png) ,
,
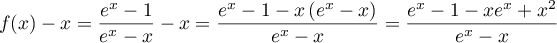 .
.
Or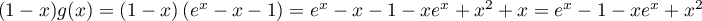 .
.
On a donc ainsi bien, pour tout![$x\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/34.png) ,
,
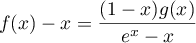 .
.
- On a vue que, pour tout
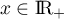 , donc aussi tout
, donc aussi tout
![$x\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/37.png) ,
, 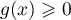 et
et 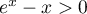 .
.
Ainsi,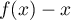 est du même signe que
est du même signe que 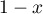 , et donc
, et donc
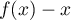 est positif sur
est positif sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/43.png) :
la courbe
:
la courbe  est au dessus de la droite
est au dessus de la droite 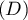 sur
sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/46.png) ,
,
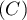 et
et 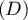 se coupant en
se coupant en 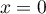 (car
(car 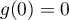 ) et en
) et en  .
.
- Pour tout
-
-
 est de la forme
est de la forme  , avec
, avec 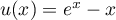 .
.
Comme, pour![$x\in[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/55.png) ,
, 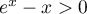 , d'après la partie A, une
primitiver de
, d'après la partie A, une
primitiver de 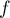 est donc
est donc
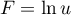 , soit
, soit 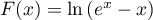 .
.
- L'aire du domaine est:
![\begin{array}{ll}\mathcal{A}&\dsp=\int_0^1\!\!\Bigl( f(x)-x\Bigr)\,dx
=\int_0^1\!\!f(x)\,dx-\int_0^1\!\!x\,dx
=\Bigl[F(x)\Bigr]_0^1-\Bigl[\dfrac12x^2\Bigr]_0^1\\[0.3cm]
&\dsp=\Bigl(F(1)-F(0)\Bigr)- \Bigl(\dfrac121^2-\dfrac120^2\Bigr)
=\ln(e-1)-\dfrac12\enar](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/60.png)
-
Partie C
-
![\psset{unit=5cm,arrowsize=7pt}
\fbox{\begin{pspicture}(-.2,-.2)(1.5,1.5)
\psline[linewidth=1.6pt]{->}(-.2,0)(1.5,0)
\psline[linewidth=1.6pt]{->}(0,-.2)(0,1.5)
\newcommand{\f}[1]{2.718 #1 exp 1 sub 2.718 #1 exp #1 sub div}
\psplot{0}{1}{\f{x}}
\newcommand{\fr}[1]{#1 10 div}
\multido{\i=-2+1}{18}{
\psline[linewidth=.8pt,linestyle=dotted](!\fr{\i}\space-.2)(!\fr{\i}\space1.5)
\psline[linewidth=.8pt,linestyle=dotted](!-.2\space\fr{\i})(!1.5\space\fr{\i})
}
\rput(-.05,-.05){$O$}
\psline(1,-.02)(1,.02)\rput(1,-.08){$1$}
\psline(-.02,1)(.02,1)\rput(-.08,1){$1$}
\rput(.9,1.05){$(C)$}
% Construction des termes de la suite
\psplot{-0.2}{1.2}{x}
\newcommand\fn[2]{%
\ifnum#1=1
\f{#2}%
\else
\f{\fn{\numexpr#1-1}{#2}}%
\fi
}
% Valeur initiale (u_0)
\def\xinit{0.5}
\def\nmax{3}
% Initialisation pour u_0
\psline[linestyle=dashed]
(\xinit,0)
(!\xinit\space\f{\xinit})
(!\f{\xinit}\space\f{\xinit})
\rput(\xinit,-0.06){$u_0$}
% Boucle pour u_1, u_2, ..., u_nmax
\multido{\i=1+1}{\nmax}{
\psline[linestyle=dashed]
(!\fn{\i}{\xinit} \space 0)
(!\fn{\i}{\xinit} \space \fn{\i}{\xinit})
(!\fn{\i}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
(!\fn{\numexpr\i+1}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
\rput(!\fn{\i}{\xinit}\space 0){$\tm$}
\rput(!\fn{\i}{\xinit}\space -0.06){$u_\i$}
}
\end{pspicture}}](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/61.png)
- Montrons par récurrence que pour tout entier
 ,
,
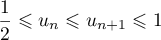 .
.
Initialisation: Pour , on a
, on a 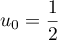 et
et 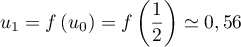 , et donc on a bien
, et donc on a bien 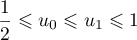 .
.
Hérédité: Supposons que pour un certain entier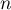 , on ait
, on ait
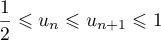 , alors,
comme la fonction
, alors,
comme la fonction 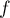 est strictement croissante sur
est strictement croissante sur ![$[0;1]](/Generateur-Devoirs/TS/ChapExponentielle/ex111-Rochambeau_c/71.png) , on a
donc
, on a
donc
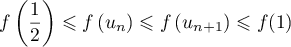 ,
,
soit aussi, comme ,
,
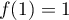 , et
, et 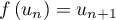 et
et 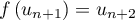 ,
,
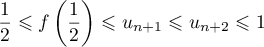 ,
,
ce qui montre que la propriété est encore vraie au rang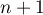 .
.
Conclusion: On vient donc de démontrer d'après le principe de récurrence que pour tout entier ,
,
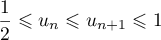 .
.
- D'après le résultat précédent, la suite
 est
croissante et majorée par 1, elle est donc convergente vers une
limite
est
croissante et majorée par 1, elle est donc convergente vers une
limite 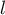 .
.
Comme la fonction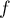 est continue sur
est continue sur  (car elle y est même
dérivable), on a alors
(car elle y est même
dérivable), on a alors
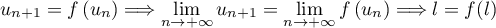
La limite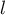 est donc une solution de l'équation
est donc une solution de l'équation 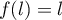 (c'est
aussi le théorème du point fixe), et il s'agit donc de l'abscisse
d'un point d'intersection de
(c'est
aussi le théorème du point fixe), et il s'agit donc de l'abscisse
d'un point d'intersection de  et
et  ,
soit
,
soit  ou
ou  d'après la question 2.b) de la partie B.
d'après la question 2.b) de la partie B.
Or, d'après la question précédente, pour tout entier ,
,
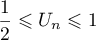 , et donc
, et donc 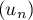 est minorée
par
est minorée
par  et ne peut pas converger vers
et ne peut pas converger vers 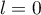 .
.
Ainsi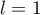 , et la suite
, et la suite 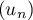 converge donc vers 1.
converge donc vers 1.
Cacher la correction
Exercice 15: Bac 2012, Centres étrangers - Résolution d'une équation avec exponentielle
(Bac S, Centres étrangers 2012, 6 points)
On considère l'équation (E) d'inconnue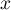 réelle :
réelle :  .
.
Partie A : Conjecture graphique
Le graphique ci-dessous donne la courbe représentative de la fonction exponentielle et celle de la fonction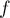 définie sur
définie sur  par
par 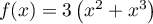 telles que les affiche une calculatrice dans un même repère orthogonal.
telles que les affiche une calculatrice dans un même repère orthogonal.
![\[
\psset{xunit=1.0cm,yunit=1.0cm,algebraic=true,dotstyle=o,dotsize=3pt 0,linewidth=0.8pt,arrowsize=3pt 2,arrowinset=0.25}
\begin{pspicture*}(-7,-6)(7,6)
\psaxes[labelFontSize=\scriptstyle,xAxis=true,yAxis=true,Dx=1,Dy=1,ticksize=-2pt 0,subticks=2]{->}(0,0)(-7,-6)(7,6)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-7.0}{7.0}{EXP(x)}
\psplot[plotpoints=2000,linewidth=1.25pt]{-7.0}{7.0}{3*(x^2+x^3)}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/6.png)
À l'aide du graphique ci-dessus, conjecturer le nombre de solutions de l'équation (E) et leur encadrement par deux entiers consécutifs.
Partie B : étude de la validité de la conjecture graphique
(Bac S, Centres étrangers 2012, 6 points)
Partie A: Conjecture. Les solutions de l'équation (E) sont les abscisses des points d'intersection des deux courbes. Il semble y en avoir 2. L'une comprise entre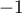 et
et  , l'autre entre 0 et 1.
, l'autre entre 0 et 1.
Partie B : étude de la validité de la conjecture graphique
Cacher la correction
On considère l'équation (E) d'inconnue
Partie A : Conjecture graphique
Le graphique ci-dessous donne la courbe représentative de la fonction exponentielle et celle de la fonction
![\[
\psset{xunit=1.0cm,yunit=1.0cm,algebraic=true,dotstyle=o,dotsize=3pt 0,linewidth=0.8pt,arrowsize=3pt 2,arrowinset=0.25}
\begin{pspicture*}(-7,-6)(7,6)
\psaxes[labelFontSize=\scriptstyle,xAxis=true,yAxis=true,Dx=1,Dy=1,ticksize=-2pt 0,subticks=2]{->}(0,0)(-7,-6)(7,6)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-7.0}{7.0}{EXP(x)}
\psplot[plotpoints=2000,linewidth=1.25pt]{-7.0}{7.0}{3*(x^2+x^3)}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/6.png)
À l'aide du graphique ci-dessus, conjecturer le nombre de solutions de l'équation (E) et leur encadrement par deux entiers consécutifs.
Partie B : étude de la validité de la conjecture graphique
-
- Étudier selon les valeurs de
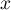 , le signe de
, le signe de  .
.
- En déduire que l'équation (E)n'a pas de solution sur l'intervalle
![$]-\infty~;~-1]$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/9.png) .
.
- Vérifier que 0 n'est pas solution de (E).
- Étudier selon les valeurs de
- On considère la fonction
 , définie pour tout nombre réel de
, définie pour tout nombre réel de ![$]-1~;~0[\cup]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/11.png) par :
par :
![\[h(x)=\ln 3+\ln\left(x^2\right)+\ln(1+x)-x.\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/12.png)
Montrer que, sur![$]-1~;~0[\: \cup\: ]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/13.png) , l'équation (E) équivaut à
, l'équation (E) équivaut à 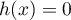 .
.
-
- Etudier les limites de
 en
en  ,
,  et
et  .
.
- Montrer que, pour tout réel
 appartenant à
appartenant à ![$]-1~;~0[~\cup~]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/20.png) , on a:
, on a:
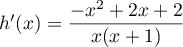
- Déterminer les variations de la fonction
 .
.
- Déterminer le nombre de solutions de l'équation
 et donner une valeur arrondie au centième de chaque solution.
et donner une valeur arrondie au centième de chaque solution.
- Conclure quant à la conjecture de la partie A.
- Etudier les limites de
Correction exercice 15
(Bac S, Centres étrangers 2012, 6 points)
Partie A: Conjecture. Les solutions de l'équation (E) sont les abscisses des points d'intersection des deux courbes. Il semble y en avoir 2. L'une comprise entre
Partie B : étude de la validité de la conjecture graphique
-
-
 ,
avec
,
avec 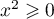 et
et 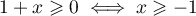 , ainis
, ainis
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ &$-\infty$ && $-1$ && $0$ && $+\infty$\\\hline
$x^2$ && $+$ &$|$&$+$&\zb&$+$& \\\hline
$1+x$ && $-$ &\zb&$+$&$|$&$+$& \\\hline
$x^3+x^2$ && $-$ &\zb&$+$&\zb&$+$& \\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/6.png)
- On a donc, pour tout
 ,
, 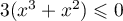 .
Or,
.
Or, 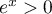 pour tout
pour tout 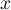 réel, et donc il ne peut pas y avoir de
solution
réel, et donc il ne peut pas y avoir de
solution 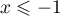 à (E)
à (E)
-
 et
et 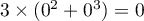 . Donc
. Donc 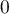 n'est pas solution de (E).
n'est pas solution de (E).
-
-
![$\forall x \in ]-1~;~0[~\cup~]0~;~+\infty[,
\begin{array}[t]{lcl}
\mbox{(E)} & \iff & e^x=3(x^2+x^3) \\
&\iff & \ln e^x=\ln\left( 3(x^2+x^3)\right) \\
&\iff & x=\ln3+\ln\left( x^2( 1+x) \right) \\
&\iff & x=\ln3+\ln\left( x^2 \right) + \ln\left(1+x\right) \\
&\iff & \ln3 + \ln\left( x^2 \right) + \ln\left( 1+x\right) -x = 0
\iff h(x) = 0 \\
\end{array} $](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/15.png)
-
- En
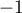 :
:  ,
et, par composition,
,
et, par composition,
 ,
et alors, par additions,
,
et alors, par additions,
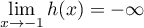 .
.
En : par composition,
: par composition,
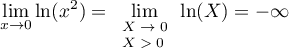 ,
et
,
et 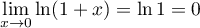 .
.
Ainsi, par addition, .
.
En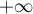 : On a, pour tout
: On a, pour tout  ,
,
![$h(x)=\ln3-x\Bigl[-2\dfrac{\ln(x)}{x}-\dfrac{\ln(1+x)}{x}+1\Bigr]$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/26.png) .
.
De plus, par croissances comparées,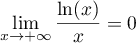 ,
et donc aussi
,
et donc aussi
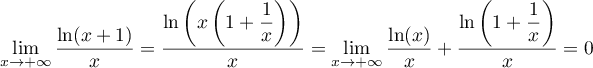 ,
,
On a alors, par addition et produit,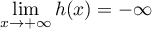 .
.
-
 est une somme et composée de fonctions de référence dérivables, donc
est une somme et composée de fonctions de référence dérivables, donc 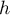 est bien dérivable sur
est bien dérivable sur ![$]-1~;~0[~\cup~]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/32.png) .
.
Plus précisément, pour tout réel![$x\in]-1;0[\cup]0;+\infty[,$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/33.png) on a
on a
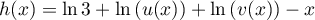 ,
,
avec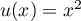 , donc
, donc  , et
, et 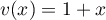 , donc
, donc 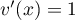 ,
et ainsi,
,
et ainsi,
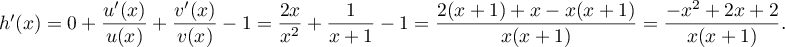
- Le numérateur de
 est un trinôme du second degré qui a
pour discriminant
est un trinôme du second degré qui a
pour discriminant 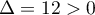 et qui admet donc deux racines
et qui admet donc deux racines 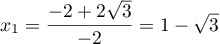 et
et  .
.
Le dénominateur est aussi un trinôme du second degré dont les racines sont mises en évidence: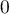 et
et 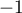 .
.
![\[\begin{tabular}{|c|ccccccccc|}\hline
$x$ & $-1$ && $1-\sqrt{3}$ && $0$&& $ 1+\sqrt{3} $&&$+\infty$\\\hline
$-x^2+2x+2$ && $-$ & $0$ && $+$ & &$0$
&$-$&\\\hline $x(x+1)$ & $0$ && $-$&&$0$ & &$+$ &&\\\hline
$h'(x)$ & $\mid\mid$ & $+$ & $0$ &$-$ &$\mid\mid$&$ + $ &$ 0 $ &$-$& \\\hline
&&&&&&&&&\\
$h$&
\psline(0,.8)(0,-.6)\,\psline(0,.8)(0,-.6)&
\psline[arrowsize=7pt]{->}(-.2,-.3)(.7,.4)
&&
\psline[arrowsize=7pt]{->}(-.7,.4)(.3,-.3)
&
\psline(0,.8)(0,-.6)\,\psline(0,.8)(0,-.6)&
\psline[arrowsize=7pt]{->}(-.2,-.3)(.7,.4)
&&
\psline[arrowsize=7pt]{->}(-.7,.4)(.3,-.3)
&
\\
&\qquad\ \scriptsize$-\infty$\hspace*{-2em}&&&\quad\scriptsize$-\infty$\hspace*{-2em}
&\qquad\ \scriptsize$-\infty$\hspace*{-2em}&&&\quad\scriptsize$-\infty$\hspace*{-3em}&
\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/46.png)
-
- Sur l'intervalle
![$ ]-1;0[ $](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/47.png) ,
, 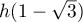 est un maximum pour
est un maximum pour  .
Or
.
Or 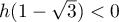 donc l'équation
donc l'équation 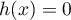 n'a pas de solution sur
n'a pas de solution sur ![$]-1;0[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/52.png) .
C'est une première contradiction avec la conjecture de la partie A.
.
C'est une première contradiction avec la conjecture de la partie A.
- Sur l'intervalle
![$ ]0 ~;~ 1+\sqrt{3}[ $](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE_c/53.png) la fonction
la fonction  est
dérivable, donc continue, strictement croissante, et
est
dérivable, donc continue, strictement croissante, et  est compris entre
est compris entre
 et
et 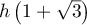 , d'après le théorème
de la bijection, l'équation
, d'après le théorème
de la bijection, l'équation  admet une unique solution
admet une unique solution
 sur
sur  .
.
La calculatrice donne: et
et
 ,
et donc
,
et donc  .
On trouve de même que
.
On trouve de même que 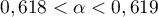 Une valeur approchée de
Une valeur approchée de 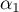 , arrondie au centième est donc
, arrondie au centième est donc 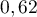 .
.
- De même sur
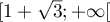 , où
, où 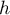 est continue et
strictement décroissante, on aune unique solution
est continue et
strictement décroissante, on aune unique solution 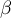 ,
avec, à l'aide de la calculatrice,
,
avec, à l'aide de la calculatrice,

- Sur l'intervalle
- La conjecture émise à la partie A était fausse: il y a bien deux solutions mais pas là où on les pensait.
- En
Cacher la correction
Exercice 16: Bac 2013 - Fonction avec log, dérivée, limites, TVI, algorithme, intégrale
Bac S, 20 juin 2013, 7 points
Sur le graphique ci-dessous, on a tracé, dans le plan muni d'un repère orthonormé , la courbe représentative
, la courbe représentative  d'une fonction
d'une fonction
 définie et dérivable sur l'intervalle
définie et dérivable sur l'intervalle  .
.

On dispose des informations suivantes :

Cacher la correction
Sur le graphique ci-dessous, on a tracé, dans le plan muni d'un repère orthonormé

On dispose des informations suivantes :
- les points A, B, C ont pour coordonnées respectives (1 , 0), (1 , 2), (0 , 2);
- la courbe
 passe par le point B et la droite (BC)
est tangente à
passe par le point B et la droite (BC)
est tangente à  en B;
en B;
- il existe deux réels positifs
 et
et  tels que pour tout réel
strictement positif
tels que pour tout réel
strictement positif  ,
,

-
- En utilisant le graphique, donner les valeurs de
 et
et
 .
.
- Vérifier que pour tout réel strictement positif
 ,
,
 .
.
- En déduire les réels
 et
et  .
.
- En utilisant le graphique, donner les valeurs de
-
- Justifier que pour tout réel
 appartenant à l'intervalle
appartenant à l'intervalle
 a le même signe que
a le même signe que  .
.
- Déterminer les limites de
 en 0 et en
en 0 et en  .
On pourra remarquer que pour tout réel
.
On pourra remarquer que pour tout réel
 strictement positif,
strictement positif,  .
.
- En déduire le tableau de variations de la fonction
 .
.
- Justifier que pour tout réel
-
- Démontrer que l'équation
 admet une unique solution
admet une unique solution
 sur l'intervalle
sur l'intervalle  .
.
- Par un raisonnement analogue, on démontre qu'il existe un
unique réel
 de l'intervalle
de l'intervalle  tel que
tel que
 .
Déterminer l'entier
.
Déterminer l'entier  tel que
tel que  .
.
- Démontrer que l'équation
- On donne l'algorithme ci-dessous.

- Faire tourner cet algorithme en complétant le tableau
ci-dessous que l'on recopiera sur la copie.

- Que représentent les valeurs affichées par cet algorithme ?
- Modifier l'algorithme ci-dessus pour qu'il affiche les deux
bornes d'un encadrement de
 d'amplitude
d'amplitude 
- Faire tourner cet algorithme en complétant le tableau
ci-dessous que l'on recopiera sur la copie.
- Le but de cette question est de démontrer que la courbe
 partage le rectangle OABC en deux domaines d'aires
égales.
partage le rectangle OABC en deux domaines d'aires
égales.
- Justifier que cela revient à démontrer que
 .
.
- En remarquant que l'expression de
 peut s'écrire
peut s'écrire
 ,
terminer la démonstration.
,
terminer la démonstration.
- Justifier que cela revient à démontrer que
Correction exercice 16

-
- Comme
 , on a
, on a  .
.
De plus, est tangente à
est tangente à  en
en  , soit
donc en
, soit
donc en  .
Comme
.
Comme  est horizontale, son coeffient directeur est nul,
ce qui est la définition même du nombre dérivé de
est horizontale, son coeffient directeur est nul,
ce qui est la définition même du nombre dérivé de  en
en  .
.
On a donc ainsi .
.
-
 est de la forme
est de la forme  , avec
, avec
 , soit
, soit
 ,
et
,
et
 , soit
, soit  .
.
Ainsi, , et donc,
pour tout
, et donc,
pour tout  ,
,

- En déduire les réels
 et
et  .
.
 ,
or
,
or  d'après 1.a.,
et donc on a directement
d'après 1.a.,
et donc on a directement  .
.
 ,
or
,
or  d'après 1.a.,
et donc on a aussi
d'après 1.a.,
et donc on a aussi  .
.
On a donc finalement , et
pour tout
, et
pour tout  ,
,
 .
.
- Comme
-
- D'après 1.b., on a pour tout
 ,
,
 .
.
Comme et
et  ,
,
 a donc le même signe que
a donc le même signe que  .
.
-
Limite en
 :
:
 ,
et
,
et  ,
,
d'où par produit des limites, .
.
Limite en :
Pour tout réel
:
Pour tout réel  ,
,
 .
.
 ,
et, par croissance comparée en l'infini
,
et, par croissance comparée en l'infini
 ,
,
d'où, par addition des limites, .
.
-
 est du signe de
est du signe de  ,
or
,
or  , car la fonction
, car la fonction  est
strictement croissante sur
est
strictement croissante sur  .
.

- D'après 1.b., on a pour tout
-
- La fonction
 est continue et strictement croissante sur
est continue et strictement croissante sur
 ,
avec
,
avec  et
et
 .
.
On en déduit donc, d'après le théorème des valeurs intermédiaires, qu'il existe un unique tel que
tel que
 .
.
- A l'aide de la calculatrice (par balayage, avec un tableau de
valeurs par exemple),
on a
 ,
,
 ,
,
 ,
,
 ,
et
,
et  .
Ainsi,
.
Ainsi,  , car
, car  est
strictement décroissante sur
est
strictement décroissante sur  .
L'entier
.
L'entier  recherché est donc
recherché est donc  .
.
- La fonction
-
-

- Cet algorithme affiche les valeurs
 et
et  (les dernières valeurs prises par
(les dernières valeurs prises par  et
et  ).
).
Ces valeurs sont les bornes d'un encadrement de d'amplitude inférieure ou égale à
d'amplitude inférieure ou égale à  .
.
- Modifier l'algorithme ci-dessus pour qu'il affiche les deux
bornes d'un encadrement de
 d'amplitude
d'amplitude 
Pour toruver un encadrement de plutôt que de
plutôt que de  ,
on débute par l'encadrement
,
on débute par l'encadrement  et
et  (d'après la question 3.b..
(d'après la question 3.b..
De plus, comme est décroissante sur
est décroissante sur  ,
donc sur
,
donc sur  ,
on doit aussi modifier le test "
,
on doit aussi modifier le test " en
"
en
" ".
".
L'algorithme devient ainsi (il y d'autres possibilités menant au même résultat):

-
- Le but de cette question est de démontrer que la courbe
 partage le rectangle OABC en deux domaines d'aires
égales.
partage le rectangle OABC en deux domaines d'aires
égales.
- L'aire du rectangle
 vaut
vaut  .
.
Soit le point d'intersection de
le point d'intersection de  avec l'axe des abscisses.
On cherche alors à montrer que
avec l'axe des abscisses.
On cherche alors à montrer que

 est l'abscisse du point
est l'abscisse du point  tel que
tel que

Le problème considéré revient donc bien à montrer que .
.
- On a
 .
.
Ainsi, .
.
 est une primitive de
est une primitive de  ,
tandis que
,
tandis que  est de la forme
est de la forme
 , avec
, avec  , et ainsi,
, et ainsi,
 est une primitive
de
est une primitive
de  .
.
On a donc,

ce qui montre donc bien la propriété souhaitée.
- L'aire du rectangle
Cacher la correction
Exercice 17: Bac 2013: ROC, limites, asymptote oblique, suite
Le but de l'exercice est l'étude de la suite  définie par son
premier terme
définie par son
premier terme  , puis pour tout entier
, puis pour tout entier  ,
,
 .
.
Partie A. Restitution organisée des connaissances.
On rappelle que .
.
Montrer que  .
.
Partie B.
On considère la fonction  définie sur
définie sur  par
par  .
.
On note sa courbe représentative.
sa courbe représentative.
Partie C.
(Bac 2013, métropole)
Partie A. ROC. On pose .
Ainsi,
.
Ainsi,

et donc, , par quotient des limites.
, par quotient des limites.
Partie B. On considère la fonction définie sur
définie sur  par
par  .
.
Partie C.
Cacher la correction
On rappelle que
On note
- Soit
 la fonction définie sur
la fonction définie sur  par
par
 .
.
Montrer que la fonction est négative sur
est négative sur  et positive sur
et positive sur
 .
.
-
- Montrer que pour tout
 ,
,  .
.
- En déduire le sens de variation de
 .
.
- Montrer que la droite
 d'équation
d'équation  est une asymptote
à la courbe
est une asymptote
à la courbe  en
en  .
.
- Etudier la position de la courbe
 par rapport à la droite
par rapport à la droite
 .
.
- Montrer que pour tout
Partie C.
- Que peut-on dire de la suite
 si
si  ?
?
- On suppose que
 .
.
- Montrer que pour tout entier
 ,
,  .
.
- On note
 la fonction définie sur
la fonction définie sur  par
par
 .
.
Donner le signe de .
En déduire le sens de variation de
.
En déduire le sens de variation de  .
.
- Déduire de ce qui précède que la suite
 est
convergente et donner sa limite.
est
convergente et donner sa limite.
- Montrer que pour tout entier
- On suppose que
 .
Dans quel intervalle se trouve alors
.
Dans quel intervalle se trouve alors  ?
?
Que peut-on alors en déduire quant au sens de variation de et à sa convergence ?
et à sa convergence ?
Correction exercice 17
(Bac 2013, métropole)
Partie A. ROC. On pose

et donc,
 , par quotient des limites.
, par quotient des limites.
Partie B. On considère la fonction
- Soit
 la fonction définie sur
la fonction définie sur  par
par
 .
.
Pour , on a
, on a  , et donc,
, et donc,  ,
et comme
,
et comme  , on a alors
, on a alors  .
.
Pour ,
,  et
et  , d'où
, d'où  .
.
Remarque: on peut tout aussi bien dériver et étudier
son sens de variation et montrer ainsi que
et étudier
son sens de variation et montrer ainsi que  est le minimum de
est le minimum de
 sur
sur  .
.
-
- Pour tout
 ,
,
 ,
avec
,
avec
 et donc,
et donc,

Ainsi, ,
soit, pour
,
soit, pour  ,
,

- D'après les deux questions précédentes, on a donc que
 estr strictement croissante sur
estr strictement croissante sur  et strictement
croissante sur
et strictement
croissante sur  .
.
-
 ,
et donc, par croissance comparée (ou la partie A.),
on a
,
et donc, par croissance comparée (ou la partie A.),
on a  ,
et ainsi,
,
et ainsi,  est une asymptote à la courbe
est une asymptote à la courbe  en
en  .
.
-
 .
.
Pour ,
,  , et donc
, et donc  est au-dessus de
est au-dessus de  .
Pour
.
Pour  ,
,  , et donc,
, et donc,  est au-dessous de
est au-dessous de  .
.
- Pour tout
Partie C.
- Si
 , alors
, alors  , et donc de même
, et donc de même  ,
…
Si
,
…
Si  , la suite
, la suite  est constante et égale à
est constante et égale à  .
.
- On suppose que
 .
.
- Montrons par récurrence que pour tout entier
 ,
,  .
.
La propriété est initialement vraie car on suppose justement que .
.
Hérédité: Supposons docn que pour un entier , on ait
, on ait  .
.
Alors, comme est strictement croissante sur
est strictement croissante sur  avec
avec
 ,
on a donc,
,
on a donc,  , et la propriété est encore
vraie au rang
, et la propriété est encore
vraie au rang  .
.
Finalement, d'après le principe de récurrence, pour tout entier ,
,  .
.
-
 est positif lorsque
est positif lorsque  ,
et est négatif lorsque
,
et est négatif lorsque  .
.
Ainsi, comme pour tout entier ,
,  ,
on a
,
on a
 et ainsi la suite
et ainsi la suite  est décroisssante.
est décroisssante.
- D'après de ce qui précède que la suite
 est
décroissante et minorée par
est
décroissante et minorée par  :
elle est donc convergente vers une limite
:
elle est donc convergente vers une limite  .
.
D'après le théorème du point fixe, on a alors, .
.
- Montrons par récurrence que pour tout entier
- Si
 , alors
, alors  ,
soit
,
soit  .
.
Ainsi, toute l'étude et les résultats précédents sont encore vrais à partir de :
:
 est décroissante et converge vers
est décroissante et converge vers  .
.
Cacher la correction
Quelques autres devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
Quelques exercices corrigés
Exercices corrigés
Bac 2022 (11 mai): Exponentielle et suite récurrente
Exercices corrigés
Inégalité (de cours) avec une exponentielle
Exercices corrigés
variations et TVI
Exercices corrigés
Fonction rationnelle en exponentielle
Exercices corrigés
Encadrement de e
Voir aussi: