Oral du bac: primitive, intégration par parties, logarithme, suite
Terminale générale, spécialité mathématiques
- L'utilisation d'une calculatrice est autorisée.
- La qualité des raisonnements, de l'expression, et la précision des justifications prendront une part importante dans l'appréciation de l'interrogation orale.
- Il s'agit d'une épreuve orale: il n'est pas indispensable de rédiger l'ensemble des réponses, des calculs, du raisonnement …
Par contre vous devez être en mesure d'apporter toutes les justifications nécessaires.
L'exposé de la méthode et du raisonnement sera pris en compte.
Exercice 1: Logarithme et son carré, intégration par parties
Les courbes C et C' données ci-dessous représentent respectivement, dans un repère orthonormal 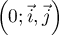 , les fonctions
, les fonctions 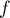 et
et 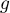 définies sur l'intervalle
définies sur l'intervalle ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/4.png) par
par 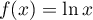 et
et 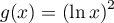 .
.
![\[\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-3.2)(4,3.2)
\newcommand{\f}[1]{x ln}
\newcommand{\g}[1]{x ln 2 exp}
\pscustom{
\psplot{1}{2.718}{\f{x}} \gsave
\psplot{2.718}{1}{\g{x}}
\fill[fillstyle=solid,fillcolor=lightgray]
%\fill[fillstyle=vlines]
\grestore}
\psline(-.2,0)(4,0)
\psline(0,-3)(0,3)
\multido{\i=1+1}{4}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\multido{\i=-3+1}{7}{\psline(-.1,\i)(.1,\i)\rput[r](-.1,\i){\i}}
\psplot{.05}{4}{\f{x}}
\psplot{.1}{4}{\g{x}}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/7.png)
Bac juin 2008
Cacher la correction
![\[\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-3.2)(4,3.2)
\newcommand{\f}[1]{x ln}
\newcommand{\g}[1]{x ln 2 exp}
\pscustom{
\psplot{1}{2.718}{\f{x}} \gsave
\psplot{2.718}{1}{\g{x}}
\fill[fillstyle=solid,fillcolor=lightgray]
%\fill[fillstyle=vlines]
\grestore}
\psline(-.2,0)(4,0)
\psline(0,-3)(0,3)
\multido{\i=1+1}{4}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\multido{\i=-3+1}{7}{\psline(-.1,\i)(.1,\i)\rput[r](-.1,\i){\i}}
\psplot{.05}{4}{\f{x}}
\psplot{.1}{4}{\g{x}}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/7.png)
- On cherche à déterminer l'aire A (en unités d'aire) de la partie grisée.
On note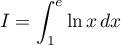 et
et 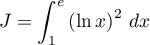 .
.
- Vérifier que la fonction
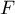 définie sur l'intervalle
définie sur l'intervalle ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/11.png) par
par
 est une primitive de la fonction logarithme népérien.
En déduire
est une primitive de la fonction logarithme népérien.
En déduire 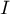 .
.
- Démontrer à l'aide d'une intégration par partie que
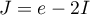 .
.
- Donner la valeur de A.
- Vérifier que la fonction
- Pour
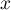 appartenant à l'intervalle
appartenant à l'intervalle ![$[1;e]$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/16.png) , on note
, on note 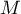 le point de la courbe C d'abscisse
le point de la courbe C d'abscisse 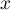 et
et  le point de la courbe C' de même abscisse.
le point de la courbe C' de même abscisse.
Pour quelle valeur de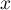 la distance MN est-elle maxiale ?
Calculer la valeur maximale de MN.
la distance MN est-elle maxiale ?
Calculer la valeur maximale de MN.
Correction exercice 1
Bac juin 2008
-
- On dérive:
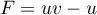 avec
avec 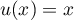 donc
donc  et
et 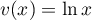 donc
donc  ,
,
et alors,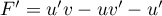 ,
,
soit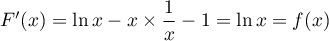
ce qui montre que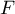 est bien une primtive de
est bien une primtive de 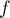 .
.
On en déduit
![\[\begin{array}{ll}I&=\dsp\int_1^e\ln x\,dx
=\Bigl[\,F(x)\,\Bigr]_1^e
=F(e)-F(1)\\[1em]
&=\left( e\ln e-e\rp-\left( 1\ln 1-1\rp
=1\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/10.png)
- On pose
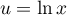 donc
donc 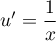 et
et 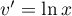 donc
donc 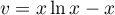 et et alors, en intégrant par parties,
et et alors, en intégrant par parties,
![\[\begin{array}{ll}J&=\Bigl[\ln x\left( x\ln x-x\rp\Bigr]_1^e
-\dsp\int_1^e\dfrac1x\left( x\ln x-x\rp\\[1em]
&=0-\dsp\int_1^e\lp\ln x-1\rp\,dx\\[1em]
&=-\dsp\int_1^e\ln x\,dx+\int_1^e1dx\\[1em]
&=-I+e-1=e-2I\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/15.png)
car .
.
- On en déduit la valeur de A:
![\[\begin{array}{ll}A&=\dsp\int_1^e\left( f(x)-g(x)\rp\,dx\\[1em]
&=\dsp\int_1^ef(x)\,dx-\int_1^eg(x)\,dx\\[1em]
&=I-J
=1-\left( e-2I\rp\\
&=1-\left( e-2\rp=3-e\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/17.png)
- On dérive:
- Pour
![$x\in[1;e]$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/18.png) , on a
, on a
![\[\begin{array}{ll}MN&=d(x)=f(x)-g(x)\\[.5em]&=\ln x-\lp\ln x\rp^2\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/19.png)
Pour trouver le maximum de cette fonction, il suffit de connaître ses variations.
On a
![\[d'(x)=\dfrac1x-2\dfrac1x\ln x=\dfrac1x\lp1-2\ln x\rp\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/20.png)
avec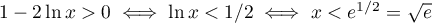 et donc
et donc
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ &$1$ && $\sqrt{e}$ && $e$\\\hline
$1/x$ && $+$ &$|$&$+$&\\\hline
$1-2\ln x$ && $+$ &\zb&$-$&\\\hline
$d'(x)$ && $+$ &\zb&$-$&\\\hline
&&&$d\lp\sqrt{e}\rp$&&\\
$d$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/22.png)
La distance est donc maximale en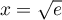 et cette distance maximale est
et cette distance maximale est
![\[d\lp\sqrt{e}\rp=\ln\sqrt{e}-\lp\ln\sqrt{e}\rp^2
=\dfrac12-\lp\dfrac12\rp^2=\dfrac14\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/24.png)
Cacher la correction
Exercice 2: Suite récurrente et suite auxiliaire géométrique
Soit la suite 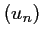 définie par
définie par
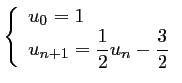 .
.
Cacher la correction
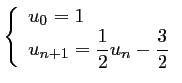 .
.
- Calculer
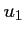 et
et 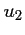 .
.
- On considère la suite
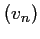 définie par
définie par
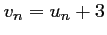 .
.
Montrer que la suite
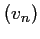 est géométrique.
est géométrique.
- En déduire une expression de
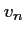 en fonction de
en fonction de 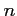 ,
puis de
,
puis de 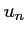 en fonction de
en fonction de 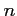 .
.
- Etudier les variations de la suite
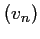 puis de la suite
puis de la suite
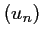 .
.
Correction exercice 2
-
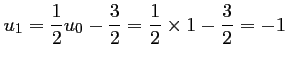 ;
;
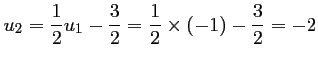 ;
;
-
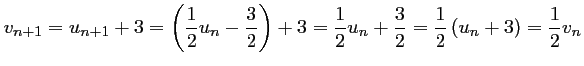 .
.
Ainsi, la suite
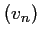 est géométrique de raison
est géométrique de raison 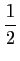 .
.
- On en déduit que pour tout entier naturel
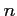 ,
,
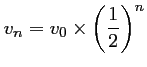 ,
avec
,
avec
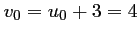 ,
d'où,
,
d'où,
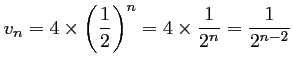 .
.
On a alors,
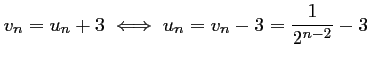 .
.
- Comme
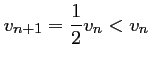 , la suite
, la suite 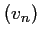 est
décroissante.
est
décroissante.
On a donc aussi,
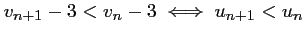 , et donc la
suite
, et donc la
suite 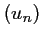 est aussi décroissante.
est aussi décroissante.
Cacher la correction
Quelques autres devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
Quelques exercices corrigés
Exercices corrigés
Limites de 2 suites
Exercices corrigés
Limites de 4 suites
Exercices corrigés
Une petite récurrence
Exercices corrigés
Une petite récurrence
Exercices corrigés
Suite auxiliaire géométrique
Voir aussi: