Oral du bac: logarithme et suites
Terminale générale, spécialité mathématiques
- L'utilisation d'une calculatrice est autorisée.
- La qualité des raisonnements, de l'expression, et la précision des justifications prendront une part importante dans l'appréciation de l'interrogation orale.
- Il s'agit d'une épreuve orale: il n'est pas indispensable de rédiger l'ensemble des réponses, des calculs, du raisonnement …
Par contre vous devez être en mesure d'apporter toutes les justifications nécessaires.
L'exposé de la méthode et du raisonnement sera pris en compte.
Exercice 1: Fonction logarithme népérien, variations et limites
Soit 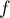 la fonction définie sur
la fonction définie sur ![$]0;+\infty[](/Generateur-Devoirs/TS/ChapLogarithme/exOral01/2.png) par
par  .
.
Etudier la fonction 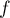 (Sens de variation et limites aux bornes de l'ensemble de définition).
(Sens de variation et limites aux bornes de l'ensemble de définition).
Cacher la correction
Correction exercice 1
- Pour tout
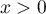 ,
, 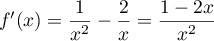 .
.
![\begin{tabular}{|c|ccccc|}\hline
$x$ & $0$ &&$\dfrac12$&& $+\infty$ \\\hline
$1-2x$ && $+$ &\zb& $-$ &\\\hline
$x^2$ &\db& $+$ &$|$& $+$ &\\\hline
$f'(x)$ &\db& $-$ &\zb& $+$ &\\\hline
&&&$-1+2\ln(2)$&&\\
$g$ && \psline[arrowsize=7pt]{->}(-.6,-.4)(.6,.4)&&
\psline[arrowsize=7pt]{->}(-.6,.4)(.6,-.4)&\\
&$-\infty$&&&&$-\infty$\\\hline
\end{tabular}](/Generateur-Devoirs/TS/ChapLogarithme/exOral01_c/3.png)
Limite en 0: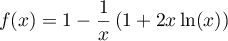 ,
avec, par croissances comparées,
,
avec, par croissances comparées,
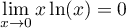 , donc
, donc
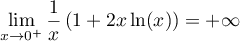 ,
et alors,
,
et alors,
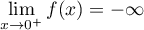 .
.
Limite en :
:  et
et 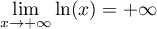 .
.
Ainsi, par addition des limites,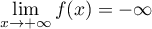 .
.
Cacher la correction
Exercice 2: Suite récurrente arithmético-géométrique - Suite auxiliaire géométrique
On considère la suite 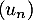 définie par son premier terme
définie par son premier terme
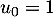 et par la relation, pour tout entier naturel
et par la relation, pour tout entier naturel  ,
,
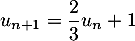 .
.
On considère la suite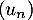 définie par son premier terme
définie par son premier terme
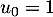 et par la relation, pour tout entier naturel
et par la relation, pour tout entier naturel 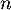 ,
,
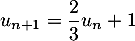 .
.
Cacher la correction
- Calculer
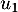 et
et 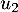 .
.
- Montrer que
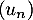 n'est ni arithmétique, ni géométrique.
n'est ni arithmétique, ni géométrique.
- On pose, pour tout entier naturel
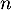 ,
,
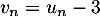 .
.
- Montrer que
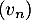 est une suite géométrique,
dont on précisera le premier terme et la raison.
est une suite géométrique,
dont on précisera le premier terme et la raison.
- Exprimer
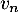 en fonction de
en fonction de 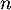 .
.
- En déduire l'expression de
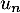 en fonction de
en fonction de 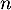 .
.
- Montrer que
Correction exercice 2
On considère la suite
-
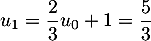 et
et 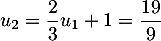 .
.
- On a
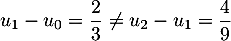 donc
donc 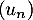 n'est pas arithmétique.
n'est pas arithmétique.
De même,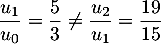 donc
donc 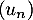 n'est pas géométrique non plus.
n'est pas géométrique non plus.
- On pose, pour tout entier naturel
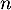 ,
,
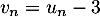 .
.
- Pour tout entier
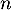 ,
,
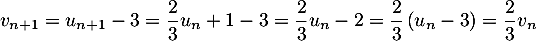 .
.
Ainsi,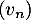 est une suite géométrique de raison
est une suite géométrique de raison 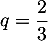 et de premier terme
et de premier terme 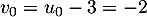 .
.
- On en déduit que, pour tout entier
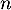 ,
,
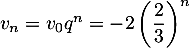 .
.
- On obtient alors,
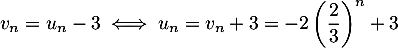 .
.
- Pour tout entier
Cacher la correction
Quelques autres devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
Quelques exercices corrigés
Exercices corrigés
Limites de 2 suites
Exercices corrigés
Limites de 4 suites
Exercices corrigés
Une petite récurrence
Exercices corrigés
Une petite récurrence
Exercices corrigés
Suite auxiliaire géométrique
Voir aussi: