Bac 2019 (Antille-Guyane): Fonction avec exponentielle, éléments graphiques, étude et primitive
Exercice corrigé - Spécialité maths, terminale générale
Partie A
Soit
La courbe
La courbe
![\[\psset{xunit=0.675cm,yunit=4.8cm,comma=true}
\begin{pspicture}(-1,-0.05)(20,1,2)
\psaxes[linewidth=1.25pt,Dy=0.1]{->}(0,0)(0,0)(20,1.2)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{20}{1 1 2.71828 x 0.2 mul neg exp add div}
\psplot[plotpoints=2000,linewidth=1.25pt]{0}{14}{x 0.05 mul 0.5 add}
\psdots(10,1)\uput[ul](10,1){B}
\uput[u](17,0.95){\blue $\mathcal{C}_f$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019/10.png)
- Justifier que
 .
.
On obtient alors, pour tout réel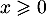 ,
,
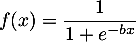 .
.
- On admet que la fonction
 est dérivable sur
est dérivable sur  et on note
et on note 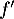 sa fonction
dérivée.
sa fonction
dérivée.
Vérifier que, pour tout réel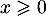
![\[f'(x)=\dfrac{be^{-bx}}{\lp1+e^{-bx}\rp^2}.\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019/18.png)
- En utilisant les données de l'énoncé, déterminer
 .
.
Partie B
La proportion d'individus qui possèdent un certain type d'équipement dans une population est modélisée par la fonction
Le réel
Le nombre
Ainsi, pour ce modèle,
- Quelle est, pour ce modèle, la proportion d'individus équipés au 1er janvier 2010? On en donnera une valeur arrondie au centième.
-
- Déterminer le sens de variation de la fonction
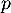 sur
sur  .
.
- Calculer la limite de la fonction
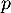 en
en 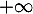 .
.
- Interpréter cette limite dans le contexte de l'exercice.
- Déterminer le sens de variation de la fonction
- On considère que, lorsque la proportion d'individus équipés dépasse 95 %, le marché est saturé. Déterminer, en expliquant la démarche, l'année au cours de laquelle cela se produit.
-
- Vérifier que, pour tout réel
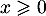 ,
,
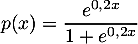 .
.
- En déduire une primitive
 de la fonction
de la fonction 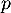 .
.
- La proportion moyenne d'individus équipés entre 2008 et 2010
est donnée par le nombre
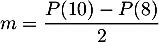 .
Déterminer une valeur arrondie au centième de
.
Déterminer une valeur arrondie au centième de 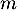 .
.
- Vérifier que, pour tout réel
Correction
Partie A
Partie B
Cacher la correction
Partie A
-

- On a
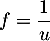 avec
avec 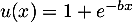 donc
donc 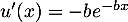
et alors , soit
, soit
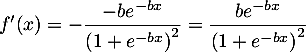
- La tangente à
 en
en  passe par
passe par
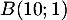 .
Le coefficient directeur de cette tangente est
donc
.
Le coefficient directeur de cette tangente est
donc
![\[m=\dfrac{1-0,5}{10-0}=\dfrac1{20}=0,05\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/10.png)
Par ailleurs, ce coefficient directeur est aussi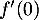 ,
et donc
,
et donc
![\[f'(0)=\dfrac{b}{\lp1+e^0\rp^2}=\dfrac{b}4=0,05
\iff b=0,2\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/12.png)
Partie B
- En 2010, on a
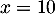 , et donc la proportion d'individus équipés
est
, et donc la proportion d'individus équipés
est 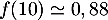 .
.
-
- Comme vu à la question 2, partie A,
on a, avec
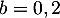 ,
,
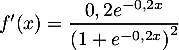 et donc, comme
et donc, comme 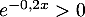 et
et
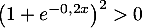 ,
la fonction
,
la fonction  est strictement croissante sur
est strictement croissante sur  donc aussi sur
donc aussi sur
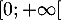 .
.
- En
 , on a
, on a
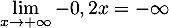 , donc par composition
, donc par composition
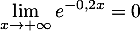 et donc, finalement
et donc, finalement
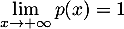 .
.
- Au bout d'un temps assez long, tout le monde va posséder ce type d'équipement.
- Comme vu à la question 2, partie A,
on a, avec
- On cherche
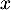 tel que
tel que
![\[\begin{array}{ll}p(x)>95\%=0,95
&\iff \dfrac{1}{1 + e^{-0,2x}}>0,95\\
&\iff 1 + e^{-0,2x}<\dfrac1{0,95}\\
&\iff e^{-0,2x}<\dfrac1{0,95}-1=\dfrac{0,05}{0,95}\\
&\iff -0,2x<\ln\lp\dfrac{0,05}{0,95}\rp\\
&\iff x>-\dfrac1{0,2}\ln\lp\dfrac{0,05}{0,95}\rp\simeq14,7
\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/27.png)
Cela se produit donc au cours de la 14ème année. -
-
![\[p(x) = \dfrac{1}{1 + e^{-0,2x}}
=\dfrac{e^{0,2x}}{e^{0,2x}}\tm\dfrac{1}{1 + e^{-0,2x}}
=\dfrac{e^{0,2x}}{1 + e^{0,2x}}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/28.png)
- Exprimer sous cette forme, on a donc
 de la forme
de la forme 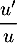 , et on trouve donc une primitive
, et on trouve donc une primitive
![\[P(x)=\dfrac1{0,2}\ln\lp1+e^{0,2x}\rp=5\ln\lp1+e^{0,2x}\rp\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/31.png)
- La proportion moyenne d'individus équipés entre 2008 et 2010
est alors
![\[m=\dfrac{P(10)-P(8)}2
=\dfrac12\left(
\dfrac1{0,2}\ln\lp1+e^{2}\right)
+
\dfrac1{0,2}\ln\lp1+e^{1,6}\rp\rp\simeq 0,86
\]](/Generateur-Devoirs/TS/ChapExponentielle/ex2019_c/32.png)
-
Cacher la correction
Tags:ExponentiellePrimitive
Voir aussi:
