Bac 2024: Vrai ou faux, limites et une équation différentielle

Exercice corrigé - Spécialité maths, terminale générale

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.

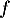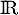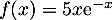  1. On considère la fonction $f$ définie sur $\R$ par : $f(x)=5 x \mathrm{e}^{-x}$.
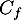    On note $C_{f}$ la courbe représentative de 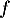$f$ dans un repère orthonormé.

    Affirmation 1 :
    L'axe des abscisses est une asymptote horizontale à la courbe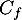 $C_{f}$.

    Affirmation 2 :
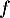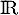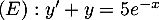    La fonction $f$ est solution sur $\R$ de l'équation différentielle $(E): y'+y=5e^{-x}$.


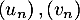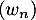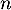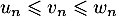  2. On considère les suites $\left( u_n\rp,\left( v_n\rp$ et $\left( w_{n}\rp$, telles que, pour tout entier naturel $n$ : $u_n \leqslant v_n \leqslant w_n$.
    De plus, la suite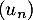 $\left( u_n\rp$ converge vers -1 et la suite 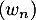$\left( w_n\rp$ converge vers 1.

    Affirmation 3 :
    La suite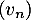 $\left( v_n\rp$ converge vers un nombre réel 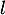$l$ appartenant à l'intervalle $[-1 ; 1]$.
    On suppose de plus que la suite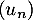 $\left( u_n\rp$ est croissante et que la suite 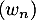$\left( w_n\rp$ est décroissante.

    Affirmation 4 :
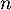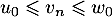    Pour tout entier naturel $n$, on a alors : $u_0 \leqslant v_n \leqslant w_0$.

Correction


Tags:QCMSuitesExponentielleÉquations différentielles

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 1 - h3: 0