Etude d'une fonction avec une exponentielle, convexité

Exercice corrigé - Spécialité maths, terminale générale

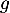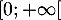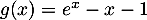On considère la fonction $g$ définie sur $[0;+\infty[$ par $g(x)=e^x-x-1$.
  1. Etudier les variations de la fonction $g$.
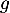  2. Déterminer le signe de 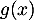$g(x)$ suivant les valeurs de $x$.
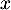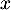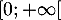  3. En déduire que pour tout $x$ de $[0;+\infty[$, $e^x>x$.
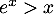  4. Étudier la convexité de la fonction $g$.

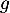Correction


Tags:ExponentielleConvexité

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 1 - h3: 0