Position relative, convexité
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction 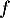 définie sur
définie sur 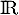 par
par 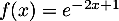 ,
et la droite
,
et la droite 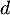 d'équation
d'équation 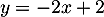 .
.
On cherche à déterminer la position relative de la courbe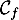 représentative de
représentative de 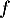 et de la droite
et de la droite 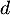 .
.
Correction
On cherche à déterminer la position relative de la courbe
- On note
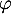 la fonction définie sur
la fonction définie sur 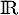 par
par 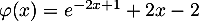 .
.
- Montrer que la fonction
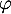 est convexe sur
est convexe sur 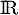 .
.
- Donner une équation de la tangente à la courbe de
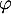 au point d'abscisse
au point d'abscisse  .
.
- Montrer que la fonction
- En utilisant les résultats précédents, donner le signe de
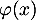 .
.
- Dresser le tableau de variation de
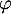 , puis retrouver le résultat
de la question précédente.
, puis retrouver le résultat
de la question précédente.
- Conclure.
Correction
Tags:ExponentielleConvexité
Voir aussi:
