Bac 2018 (Pondichéry, 4 mai): Droite, plan, intersection

Exercice corrigé - Spécialité maths, terminale générale

Dans l'espace muni du repère orthonormé 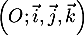$\left( O; \vec{i}, \vec{j}, \vec{k}\rp$ d'unité 1 cm, on considère les points A, B, C et D de coordonnées respectives (2 ; 1 ; 4), (4 ; -1 ; 0), (0 ; 3 ; 2) et (4 ; 3 ; -2).

Déterminer une représentation paramétrique de la droite (CD).
Soit M un point de la droite (CD).
1. Déterminer les coordonnées du point M tel que la distance BM soit minimale.
2. On note H le point de la droite (CD) ayant pour coordonnées (3 ; 3 ; - 1). Vérifier que les droites (BH) et (CD) sont perpendiculaires.
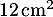3. Montrer que l'aire du triangle BCD est égale à $12\,\text{cm}^2$ .
1. Démontrer que le vecteur 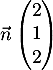$\vec{n}\begin{pmatrix}2\\1\\2\end{pmatrix}$ est un vecteur normal au plan (BCD).
2. Déterminer une équation cartésienne du plan (BCD).
3. Déterminer une représentation paramétrique de la droite $\Delta$ passant par A et orthogonale au plan (BCD).
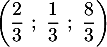4. Démontrer que le point I, intersection de la droite $\Delta$ et du plan (BCD) a pour coordonnées $\left(\dfrac{2}{3}~;~\dfrac{1}{3}~;~\dfrac{8}{3}\right)$ .
Calculer le volume du tétraèdre ABCD.

Correction

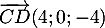$\overrightarrow{CD}(4;0;-4)$ est un vecteur directeur de la droite 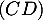, d'où la représentation paramétrique

$(CD):\la\begin{array}{ll}x=4t\\y=3\\z=2-4t\enar\right.\,, \ t\in\R$
Soit M un point de la droite (CD).
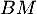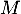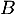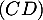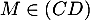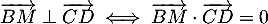1. est minimale si et seulement si est le projeté orthogonal de sur la droite : donc $M\in(CD)$ et $\overrightarrow{BM}\perp\overrightarrow{CD}\iff\overrightarrow{BM}\cdot\overrightarrow{CD}=0$ .
  Soit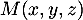 , alors il existe 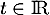$t\in\R$ tel que
  
  $M\in(CD)\iff\la\begin{array}{ll}x=4t\\y=3\\z=2-4t\enar\right. \quad\text{ et } \quad \begin{array}[t]{ll}\overrightarrow{BM}\cdot\overrightarrow{CD}&=4(x-4)+0(y+1)+(-4)(z-0)=0 \\ &\iff 4x-4z=16\end{array}$
  
  On doit donc avoir
  
  $4x-4z=4(4t)-4(2-4t)=16\iff 32t-8=16\iff t=\dfrac{24}{32}=\dfrac34$
  
  et donc finalement, .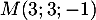
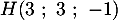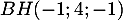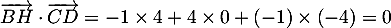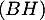2. donc et alors $\overrightarrow{BH}\cdot\overrightarrow{CD}=-1\tm4+4\tm0+(-1)\tm(-4)=0$ , ce qui montre que les droites et 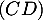sont orthogonales.
  De plus, on sait que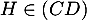 $H\in(CD)$ , donc que ces deux droites sont sécantes en .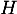
  On en déduit donc que ces deux droites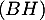 et 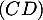sont bien perpendiculaires.
3. D'après ce qui précède, 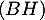est la hauteur issue de 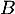dans 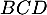, et donc
  
  $\mathcal{A}_{BCD} = \dfrac12\times CD \times BH = \dfrac12\tm\sqrt{32}\tm\sqrt{18}= \sqrt{144}= 12$
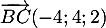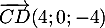1. On a $\overrightarrow{BC}(-4;4;2)$ et $\overrightarrow{CD}(4;0;-4)$ , d'où
  
  $\begin{array}{lcl} \vec{n}\cdot\overrightarrow{BC}&=&2\tm(-4)+1\tm4+2\tm2=0\\[.4em] \vec{n}\cdot\overrightarrow{CD}&=&2\tm(4)+1\tm0+2\tm(-4)=0 \enar$
  
  Ainsi, le vecteur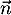 $\vec{n}$ est orthogonal à deux vecteurs non colinéaires du plan 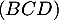et ainsi il est orthogonal à tous les vecteurs de ce plan, c'est-à-dire orthogonal au plan .
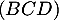2. On déduit de ce qui précède qu'une équation cartésienne du plan 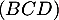s'écrit sous la forme
  
  $2x+y+2z+d=0$
  
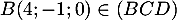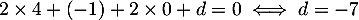  avec de plus, par exemple, $B(4;-1;0)\in(BCD)$ donc $2\tm4+(-1)+2\tm0+d=0\iff d=-7$ , d'où l'équation
  
  $2x+y+2z-7=0$
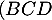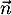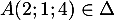3. La droite $\Delta$ est orthogonale au plan ) et donc $\vec{n}$ en est un vecteur directeur, avec de plus $A(2;1;4)\in\Delta$ , d'où une représentation paramétrique
  
  $\Delta:\la\begin{array}{ll}x=2+2t\\y=1+t\\z=4+2t\enar\right.\ , \ t\in\R$
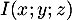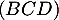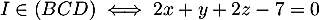4. Soit , intersection de la droite $\Delta$ et du plan , alors d'une part $I\in(BCD)\iff 2x+y+2z-7=0$ .
  D'autre part, comme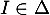 $I\in\Delta$ , et d'après la question précèdente, il existe un réel 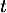tel que les coordonnées de 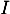vérifient les équations paramétriques de $\Delta$ .
  On a donc
  
  $2(2+2t)+(1+t)+2(4+2t)-7=0 \iff 9t+6=0\iff t=-\dfrac69=-\dfrac23$
  
  et on trouve alors les coordonnées
  
  $\la\begin{array}{ll}x=2+2\lp-\dfrac23\rp=\dfrac23\\ y=1+\lp-\dfrac23\rp=\dfrac13\\ z=4+2\lp-\dfrac23\rp=\dfrac83\enar\right.$
  
  qui sont les coordonnées recherchées.
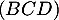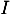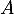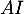Comme $\Delta$ est perpendiculaire au plan en et passe par , on en déduit que est la hauteur du tétraèdre 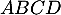de base 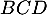, et donc

$\mathcal{V}_{ABCD} = \dfrac13\times AI\times \mathcal{A}_{ABCD} =\dfrac13\times AI\times12$

avec

$\begin{array}{ll}AI&=\sqrt{\lp\dfrac23-2\rp^2+\lp\dfrac13-1\rp^2+\lp\dfrac83-4\rp^2}\\[1.4em] &=\sqrt{\dfrac{4^2+2^2+4^2}{3^2}}=\sqrt{\dfrac{36}{3^2}}=\dfrac63=2 \enar$

d'où le volume du tétraèdre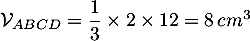 $\mathcal{V}_{ABCD}=\dfrac13\tm2\tm12=8\,cm^3$

Cacher la correction

Tag:Géométrie dans l'espace

Autres sujets au hasard:

Voir aussi:

Quelques devoirs

Devoir corrigé

Géométrie plane et exponentielle

maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente

Devoir corrigé

Géométrie plane, équation de droites

géométrie plane analytique, vecteurs et équations de droites, géométrie avec une hyperbole et ses tangentes, courbe représentative de la fonction inverse

Devoir corrigé

Géométrie dans l'espace, tangente à une courbe, étude de fonction avec exponentielle

géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle

Devoir corrigé

Géométrie dans l'espace - Étude d'une fonction rationnelle

géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle - Analyse: étude d'une fonction: variations, limites, TVI, asymptotes, ...

Devoir corrigé

Convexité et géométrie dans l'espace

étude de la convexité de fonctions (et variations, tangentes, limites, ...) et géométrie dans l'espace