Bac 2015 (Nouvelle Calédonie) - Droites perpendiculaires dans l'espace
Exercice corrigé - Spécialité maths, terminale générale
L'espace est rapporté au repère orthonormé
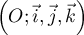 .
On désigne par
.
On désigne par  l'ensemble des
nombres réels.
l'ensemble des
nombres réels.
On rappelle que deux droites de l'espace sont dites perpendiculaires si et seulement si elles sont orthogonales et sécantes.
Soient le point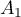 de coordonnées
de coordonnées 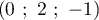 et le vecteur
et le vecteur
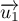 de coordonnées
de coordonnées 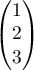 .
.
On appelle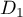 la droite passant par
la droite passant par 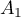 et de vecteur directeur
et de vecteur directeur
 .
.
On appelle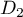 la droite qui admet pour représentation paramétrique
la droite qui admet pour représentation paramétrique
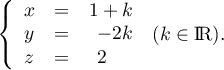
Le but de l'exercice est de prouver l'existence d'une droite perpendiculaire à la fois à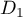 et
et 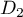 .
.
Correction
On rappelle que deux droites de l'espace sont dites perpendiculaires si et seulement si elles sont orthogonales et sécantes.
Soient le point
On appelle
On appelle
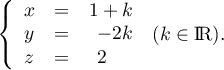
Le but de l'exercice est de prouver l'existence d'une droite perpendiculaire à la fois à
-
- Donner une représentation paramétrique de
 .
.
- Donner un vecteur directeur de
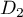 (on le notera :
(on le notera : 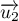 ).
).
- Le point
 appartient-il à
appartient-il à 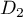 ?
?
- Donner une représentation paramétrique de
- Démontrer que les droites
 et
et 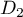 sont non coplanaires.
sont non coplanaires.
- Soit le vecteur
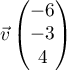 .
On définit la droite
.
On définit la droite  passant par
passant par 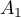 et de vecteur directeur
et de vecteur directeur 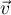 et la droite
et la droite 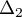 passant
par
passant
par 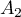 et parallèle à
et parallèle à  .
Justifier que les droites
.
Justifier que les droites 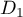 et
et  sont
perpendiculaires.
sont
perpendiculaires.
Dans la suite, on admettra que les droites et
et 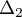 sont perpendiculaires.
sont perpendiculaires.
- Soit
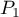 le plan défini par les droites
le plan défini par les droites 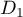 et
et  et
et
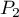 le plan défini par les droites
le plan défini par les droites  et
et  .
.
- Soit le vecteur
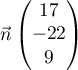 .
Vérifier que
.
Vérifier que 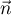 est un vecteur normal au plan
est un vecteur normal au plan  .
.
- Montrer que
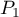 et
et 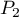 ne sont pas parallèles.
ne sont pas parallèles.
- Soit le vecteur
- Soit
 la droite d'intersection des plans
la droite d'intersection des plans 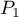 et
et
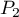 . On admettra que le vecteur
. On admettra que le vecteur 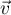 est un vecteur directeur
de
est un vecteur directeur
de 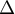 .
Utiliser les questions précédentes pour prouver qu'il existe une
droite de l'espace perpendiculaire à la fois à
.
Utiliser les questions précédentes pour prouver qu'il existe une
droite de l'espace perpendiculaire à la fois à 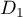 et à
et à 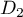 .
.
Correction
Tag:Géométrie dans l'espace
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie plane analytique, vecteurs et équations de droites, géométrie avec une hyperbole et ses tangentes, courbe représentative de la fonction inverse
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle - Analyse: étude d'une fonction: variations, limites, TVI, asymptotes, ...
étude de la convexité de fonctions (et variations, tangentes, limites, ...) et géométrie dans l'espace
