2nd degré, récurrence et théorème de comparaison

Exercice corrigé - Spécialité maths, terminale générale

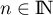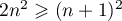  1. Déterminer les valeurs de $n\in\N telles que $2n^2\geqslant (n+1)^2.
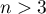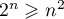  2. Montrer que, pour tout entier $n>3, $2^n\geqslant n^2.
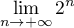  3. En déduire la limite $\dsp\lim_{n\to+\infty} 2^n.

Correction
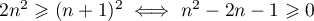  1. $2n^2\geqslant (n+1)^2 \iff n^2-2n-1\geqslant 0.
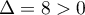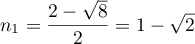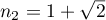    Ce trinôme du 2nd degré a pour discriminant $\Delta=8>0, et admet donc 2 racines $n_1=\dfrac{2-\sqrt{8}}{2}=1-\sqrt{2} et $n_2=1+\sqrt{2}.
    Le trinôme est ici positif à l'extérieur de ses racines, soit pour $n\in]-\infty;1-\sqrt{2}]\cup[1+\sqrt{2};+\infty[.
    Comme on s'intéresse aux solutions entières, on a donc, $2n^2\geqslant (n+1)^2 \iff n\in]-\infty;-2]\cup[3;+\infty[.
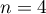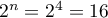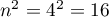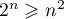  2. On peut démontrer cette propriété par récurrence: Initialisation: Pour $n=4, $2^n=2^4=16 et $n^2=4^2=16, donc on a bien $2^n\geqslant n^2 pour $n=4.
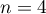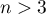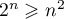    Hérédité: Supposons que pour un entier $n>3, on ait $2^n\geqslant n^2.
    Alors, au rang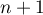 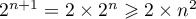$n+1, $2^{n+1}=2\times2^n\geqslant 2\times n^2, d'après l'hypothèse de récurrence.
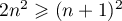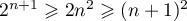    Or, d'après la question précédente, pour $n\geqslant 3, on a $2n^2\geqslant (n+1)^2, et donc, on a bien, $2^{n+1}\geqslant 2n^2\geqslant (n+1)^2.
    Ceci montre que la propriété est encore vraie au rang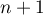 $n+1.
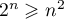    Conclusion: On vient donc de démontrer, d'après le principe de récurrence, que pour tout entier $n\geqslant 4, $2^n\geqslant n^2.
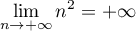  3. On sait que $\dsp\lim_{n\to+\infty}n^2=+\infty.
    Ainsi, d'après le théorème de comparaison des limites (corollaire du théorème des gendarmes), on a aussi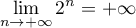 $\dsp\lim_{n\to+\infty}2^n=+\infty.


Cacher la correction


Tag:Suites

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 1 - h3: 0