Valeur d'un réel pour lequel un triangle est isocèle ou rectangle
Exercice corrigé - maths en seconde générale
Énoncé
Soit 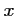 un nombre réel.
On considère les points
un nombre réel.
On considère les points 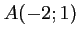 ,
, 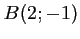 et
et 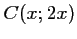 .
.
- Montrer que pour tout
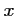 le triangle
le triangle 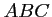 est isocèle de
sommet
est isocèle de
sommet 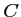 .
.
- Déterminer
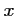 pour que le triangle
pour que le triangle 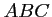 soit rectangle en
soit rectangle en
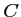 .
.
Correction
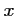 un nombre réel.
On considère les points
un nombre réel.
On considère les points 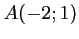 ,
, 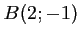 et
et 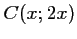 .
.
Correction
Soit
- On calcule les longueurs
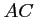 et
et 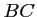 :
:
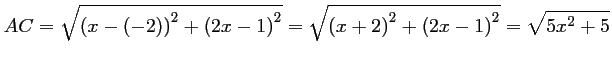
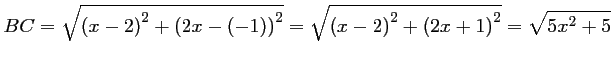
On trouve donc que, pour tout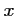 réel,
réel, 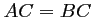 :
le triangle
:
le triangle 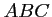 est isocèle de sommet
est isocèle de sommet 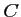 .
.
- On veut que le triangle
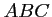 soit rectangle en
soit rectangle en 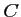 .
Alors, d'après le théorème de Pythagore,
.
Alors, d'après le théorème de Pythagore,
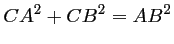
D'après la question précédente, on connaît déjà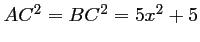 .
.
De plus,
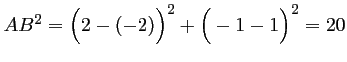 .
.
Pour que le triangle
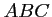 soit rectangle en
soit rectangle en 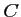 , on doit donc avoir
, on doit donc avoir
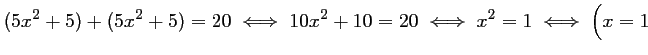 ou
ou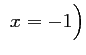
Pour que le triangle soit rectangle en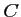 ,
on doit donc avoir
,
on doit donc avoir 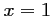 ou
ou 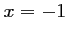 .
.
Tag:Vecteurs et coordonnées
Voir aussi:
Quelques devoirs
sur quelques équations à résoudre, systèmes d'équations à deux inconnues, et la construction géométrique graphique de points et vecteurs
sur les vecteurs et coordonnées: calculs de coordonnées, et montrer l'alignement de points. Quelques équations et un système à résoudre
résolution de systèmes d'équations, les vecteurs (vecteurs colinéaires et alignement de points), et la courbe d'une fonction
sur les systèmes d'équations, les vecteurs (vecteurs colinéaires et alignement de points), et étude du sens de variation d'une fonction
résolutions d'équations et vecteurs: représentation graphique de points et vecteurs avec des coordonnées, somme de vecteurs
