Alignement de 3 points
Exercice corrigé - maths en seconde générale
Énoncé
Soit dans un repère
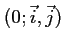 les points
les points
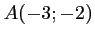 ,
,
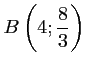 ,
,
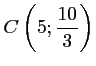 .
.
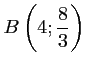 ,
,
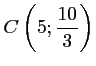 .
.
Démontrer que les points ![]() ,
, ![]() et
et ![]() sont alignés.
sont alignés.
Correction
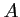 ,
, 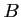 et
et 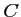 sont alignés si et seulement si les
vecteurs
sont alignés si et seulement si les
vecteurs
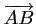 et
et
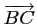 sont colinéaires.
sont colinéaires.
Correction
Les points
![]() a pour coordonnées
a pour coordonnées
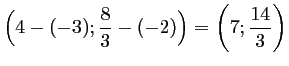
![]() a pour coordonnées
a pour coordonnées
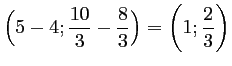 .
.
Pour ces deux vecteurs, on a:
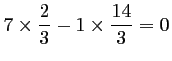 ,
ce qui montre que ces vecteurs sont colinéaires.
,
ce qui montre que ces vecteurs sont colinéaires.
Ainsi, les points ![]() ,
, ![]() et
et ![]() sont alignés.
sont alignés.
Tag:Vecteurs et coordonnées
Voir aussi:
Quelques devoirs
sur quelques équations à résoudre, systèmes d'équations à deux inconnues, et la construction géométrique graphique de points et vecteurs
sur les vecteurs et coordonnées: calculs de coordonnées, et montrer l'alignement de points. Quelques équations et un système à résoudre
résolution de systèmes d'équations, les vecteurs (vecteurs colinéaires et alignement de points), et la courbe d'une fonction
sur les systèmes d'équations, les vecteurs (vecteurs colinéaires et alignement de points), et étude du sens de variation d'une fonction
résolutions d'équations et vecteurs: représentation graphique de points et vecteurs avec des coordonnées, somme de vecteurs
