Suites récurrentes
Algorithmique / programmation en python
Suites définies explicitement, à partir d'une fonction
Exercice 1:
Définition d'une suite explicite, à partir d'une fonction - Boucles et détermination d'un seuil
- L'instruction
defpermet de définir une fonction en python. (voir éventuellement, en complément, les fonctions en python)
Qu'affiche le programme suivant ? (en python,*désigne la multiplication:3*2vaut 6, et**désigne la puissance:3**2vaut 9)def u(n): return 0.2*n**2-2 print(u(2)) n=10 print(u(n)) - Modifier le programme précédent pour qu'il calcule les termes de la suite
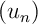 définie par l'expression
Afficher en particulier les termes
définie par l'expression
Afficher en particulier les termes .
.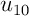 ,
,
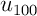 et
et
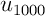 .
.
Qu'observe-t-on pour des valeurs de plus en plus grandes de n ? - Avec une boucle
for: ajouter les deux lignes suivantes au programme précédent:
Voir éventuellement à ce sujet les bouclesfor n in range(1,10): print(u(n))foret plus spécialement le paragraphe boucles sur des entiers - Détermination d'un seuil: boucle
while. Pour quelle valeur de n, les valeurs un de la suite de la question 1. dépassent-elles 1000 ?
Déterminer la valeur algébriquement, par le calcul.
Ajouter ensuite dans le programme précédent les quelques lignes suivantes:
Voir éventuellement à ce sujet les boucles conditonnellesn=0 while u(n)<1000: print(u(n)) n=n+1 print(n)while
Suites définies par récurrence
Une suite est définie par récurrence lorsque chaque terme (sauf le premier) est défini à partir du précédent (ou des précédents). Exercice 2:
- Qu'affiche le programme suivant ?
La fonction définie et utilisée ici s'appelle une fonction récursive: c'est une fonction qui s'appelle elle-même…def u(n): if n==0: return 2 else: return 3*u(n-1)-2 print(u(0)) print(u(1)) print(u(2)) n=10 print(u(n))
Donner une formule algébrique définissant par récurrence la suite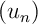 de ce programme.
de ce programme.
- Modifier le programme précédent pour qu'il calcule les termes de la suite
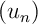 définie par l'expression
Afficher en particulier les premiers termes jusqu'à
définie par l'expression
Afficher en particulier les premiers termes jusqu'à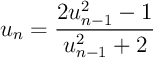 .
.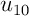 ,
puis jusqu'à
,
puis jusqu'à
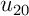 ,
et enfin jusqu'à
,
et enfin jusqu'à
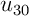 ,
,
Cette méthode de calcul est simple, fonctionne, mais n'est clairement pas efficace. Expliquer pourquoi, quelle est la difficulté ? - Une autre manière de programmer les calculs des termes d'une telle suite est d'utiliser directement la relation de récurrence reliant deux termes consécutifs:
Ce programme calcule et affiche tous les premiers termes jusqu'àu=2 n=10 for i in range(n): u=(2*u**2-1)/(u**2+2) print(u)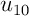 .
.
Utiliser ce programme pour afficher en particulier les termes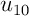 ,
,
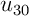 ,
et même
,
et même 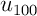 et pourquoi pas
et pourquoi pas
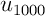 .
.
Qu'observe-t-on pour des valeurs de plus en plus grandes de n ?
Exercice 3:
Suite de Héron
Soit

- Écrire un programme qui permet de calculer et afficher les 10 premiers termes de cette suite.
- Conjecturer le sens de variation et la limite de cette suite.
- Démontrer ces résultats en faisant l'exercice complet.
Exercice 4:
On considère la suite numérique 
- On souhaite écrire un algorithme affichant, pour un entier naturel donné, tous les termes de la suite, du rang 0 au rang n .
Parmi les trois algorithmes suivants, un seul convient. Préciser lequel en justifiant la réponse.
Algorithme no1 Variables:
v est un réel
i et n sont des entiers naturels
Début de l'algorithme:
Lire n
v prend la valeur 1
Pour i variant de 1 à n faire
v prend la valeur9 6-v
Fin pour
Afficher v
Fin algorithme Algorithme no2 Variables:
v est un réel
i et n sont des entiers naturels
Début de l'algorithme:
Lire n
Pour i variant de 1 à n faire
v prend la valeur 1
v prend la valeur9 6-v
Fin pour
Afficher v
Fin algorithme Algorithme no3 Variables:
v est un réel
i et n sont des entiers naturels
Début de l'algorithme:
Lire n
v prend la valeur 1
Pour i variant de 1 à n faire
Afficher v
v prend la valeur9 6-v
Fin pour
Afficher v
Fin algorithme - Programmer l'algorithme et afficher les premiers termes de la suite. Quelle conjecture peut-on faire ? (variation, convergence, limite)
- Démontrer ces résultats en faisant l'exercice complet (exercice posé au Bac S, en 2013 au Liban).
Exercice 5:
Suite récurrente définie par une racine carrée
On considère la suite
- Calculer à l'aide d'un algorithme / programme les premiers termes de cette suite et conjecturer son sens de variation et sa limite.
- Calculs à l'aide d'un algorithme et d'une suite intermédiaire logarithmique: Démontrer les résultats précédents en faisant l'exercice complet (exercice posé au Bac S, en 2013 en Amérique du nord).
Somme des termes d'une suite
Exercice 6:
- Que calcule le programme suivant:
n=int(input("Entrer n: ")) s=0 for i in range(n+1): s=s+i print("i= ",i, " - s= ",s) - Modifier le programme précédent pour qu'il calcule, à un nombre
ndonné (ou demandé à l'utilisateur), les sommes:- 1+
+1 2
+1 3
+ … +1 4 1 n -
+1 12
+1 22
+ … +1 32 1 42
+1 20
+1 21
+1 22
+ … +1 23 1 2n
- 1+
- Quelles conjectures peut-on faire pour ces trois suites ?
Exercice 7:
On considère la suite On définit de plus, pour tout entier naturel
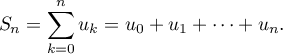
- Calculer
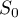 ,
, 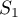 et
et 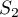 . Donner une valeur approchée des résultats à
10-2 près.
. Donner une valeur approchée des résultats à
10-2 près.
- Compléter l'algorithme suivant pour qu'il affiche la somme
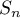 pour la valeur de l'entier
pour la valeur de l'entier 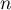 demandée à l'utilisateur.
demandée à l'utilisateur.
Entrée: n, un entier naturel Variables: u et s sont des variables réelles
n et i sont des variables entièresInitialisation: u prend la valeur 1
s prend la valeur u
i prend la valeur 0
Demander la valeur de nTraitement: Tant que ...
Affecter à i la valeur i+1
Affecter à u la valeur ...
Affecter à s la valeur ...
Fin Tant queSortie: Afficher s - Faire l'exercice complet (exercice posé au Bac S, en Nouvelle Calédonie en 2014).
Exercice 8:
Une association sportive compte 500 adhérents.
On constate que, chaque mois,
- 5% des adhérents ne renouvellent pas leur adhésion
- 30 nouveaux adhérents s'inscrivent dans l'association
- Écrire un programme qui calcule et affiche le nombre d'adhérents dans l'association mois après mois, pendant 2 ans.
- Calculer le montant total des cotisations perçues en 2 ans.
- Quel devrait être le montant de l'adhésion mensuelle pour que l'association puisse financer complètement une nouvelle installation qui coûte 20 000 euros ?
Suites récurrentes imbriquées
Exercice 9:
Deux suites imbriquéesOn définit les suites
![\[\la\begin{array}{ll}
u_{n+1}=\dfrac13u_n+\dfrac23v_n\\[.8em]
v_{n+1}=\dfrac15u_n+\dfrac45v_n\enar\right.\]](/Generateur-Devoirs/1S/Chap9/Suites-Imbriquees/6.png)
- Écrire un programme qui calcule et affiche les 10 premiers termes de ces deux suites.
- Pour tout entier
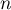 , on pose
, on pose
 .
.
Modifier le programme précédent pour qu'il calcule et affiche les 10 premiers termes de cette nouvelle suite.
Quelle conjecture peut-on faire ?
Démontrer cette conjecture. - On pose, pour tout entier
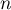 ,
,
 .
Modifier le programme précédent pour qu'il calcule et affiche les 10 premiers termes de cette nouvelle suite.
.
Modifier le programme précédent pour qu'il calcule et affiche les 10 premiers termes de cette nouvelle suite.
Quelle conjecture peut-on faire ?
Démontrer cette conjecture. - Conjecturer le comportement asymptotique des deux suites
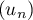 et
et  .
.
Démontrer ces résultats à l'aide des questions précédentes.
Voir éventuellement le sujet complet et corrigé
Exercice 10:
Dynamique de populations
Une grande ville de 300 000 habitants et un village de 60 000 sont à proximité.
Chaque année, 3% des habitants du village partent s'installer dans la ville tandis que
1% des habitants de la ville vont s'installer dans le village.
On note un le nombre d'habitants en ville la n-ième année et vn le nombre d'habitants du village la n-ième année.
Initialement, on a donc u0=300 000 et v0=60 000.
- Écrire un programme qui permet de calculer et d'afficher le nombre d'habitants un de la ville et du village vn pendant 10 ans.
- Conjecturer la limite de ces deux suites.
- Calculer, en modifiant le programme précédent, le nombre d'habitants en 10 ans partis de la campagne pour aller s'installer en ville.
- Modifier le programme précédent pour qu'il prenne en compte les données supplémentaires:
- chaque année, en ville, il y a 0,2% de naissances et 0,05% de morts.
- chaque année, dans le village, il y a 0,01% de naissances et 0,15% de morts.
Conjecturer avec ce nouveau modèle le comportement des populations.