Exercice corrigé Bac, Amérique du nord 2013: Suite récurrente
Calculs à l'aide d'un algorithme et d'une suite intermédiaire logarithmique
Exercice corrigé de mathématiques: Exercice corrigé Bac, Amérique du nord 2013: un exercice complet sur les suites récurrentes, démonstration par récurrence, et algorithme
Exercice - énoncé:
On considère la suite 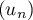 définie par
définie par 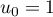 et, pour tout entier naturel
et, pour tout entier naturel 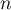 ,
,
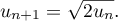
Amérique du Nord, 2013
On considère la suite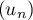 définie par
définie par 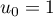 et, pour tout entier naturel
et, pour tout entier naturel 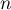 ,
,
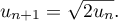
Cacher la correction
- On considère l'algorithme suivant:

- Donner une valeur approchée à
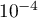 près du résultat qu'affiche cet algorithme lorsque l'on choisit
près du résultat qu'affiche cet algorithme lorsque l'on choisit 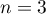 .
.
- Que permet de calculer cet algorithme ?
- Le tableau ci-dessous donne des valeurs approchées obtenues à l'aide de cet algorithme pour certaines valeurs de
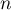 .
.
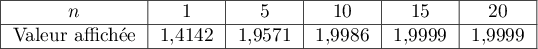
Quelles conjectures peut-on émettre concernant la suite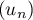 ?
?
- Donner une valeur approchée à
-
- Démontrer que, pour tout entier naturel
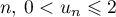 .
.
- Déterminer le sens de variation de la suite
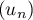 .
.
- Démontrer que la suite
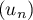 est convergente. On ne demande pas la valeur de sa limite.
est convergente. On ne demande pas la valeur de sa limite.
- Démontrer que, pour tout entier naturel
- On considère la suite
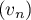 définie, pour tout entier naturel
définie, pour tout entier naturel 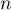 , par
, par 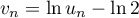 .
.
- Démontrer que la suite
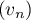 est la suite géométrique de raison
est la suite géométrique de raison  et de premier terme
et de premier terme
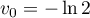 .
.
- Déterminer, pour tout entier naturel
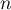 , l'expression de
, l'expression de 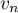 en fonction de
en fonction de 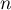 , puis de
, puis de 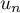 en fonction de
en fonction de 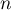 .
.
- Déterminer la limite de la suite
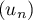 .
.
- Recopier l'algorithme ci-dessous et le compléter par les instructions du traitement et de la sortie, de façon à afficher en sortie la plus petite valeur de
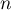 telle que
telle que 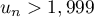 .
.

- Démontrer que la suite
Correction exercice
Amérique du Nord, 2013
On considère la suite
-
- Pour
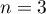 , la variable
, la variable 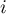 de la boucle varie de 1 à 3:
de la boucle varie de 1 à 3:
- Pour
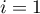 , on affecte à
, on affecte à 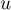 la valeur
la valeur 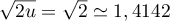
- Pour
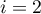 , on affecte à
, on affecte à 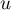 la valeur
la valeur 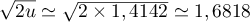
- Pour
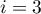 , on affecte à
, on affecte à 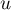 la valeur
la valeur 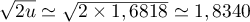
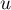 trouvée:
trouvée: 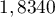 .
.
- Pour
- Cet algorithme permet de calculer et d'afficher le terme de rang
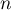 de la suite
de la suite 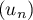 .
.
- D'après ce tableau des valeurs approchées, on peut conjecturer que la suite est croissante et converge vers 2.
- Pour
-
- Démontrons par récurrence que, pour tout entier naturel
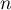 ,
, 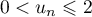 .
Initialisation: Pour
.
Initialisation: Pour 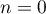 ,
, 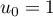 , donc on a bien
, donc on a bien 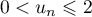 .
Hérédité: Supposons que pour un entier naturel
.
Hérédité: Supposons que pour un entier naturel 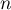 on ait
on ait 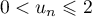 , alors,
, alors,
en multiplinat ces inégalités par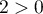 ,
, 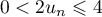 ,
,
puis, comme la fonction racine carrée est strictement croissante sur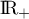 , on a
, on a 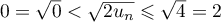 .
.
Ainsi, comme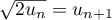 , on a donc bien encore, au rang
, on a donc bien encore, au rang
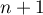 ,
, 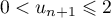 .
.
Conclusion: On vient donc de démontrer, d'après le principe de récurrence, que pour tout entier naturel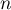 ,
,
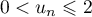 .
.
- Pour déterminer le sens de variation de la suite, on peut
procéder de (au moins) deux façons:
1ère méthode: par récurrence.
Initialisation: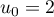 et
et 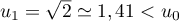 .
On a donc initialement, pour
.
On a donc initialement, pour 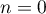 ,
, 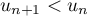 .
.
Hérédité: Supposons que pour un entier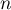 , on ait
, on ait 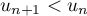 , alors,
, alors,
en multipliant par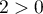 ,
, 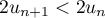 ,
,
puis, comme la fonction racine carrée est strictement croissante sur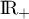 et que, d'après la question précédente,
et que, d'après la question précédente, 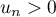 pour
tout
pour
tout 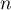 , on a donc
, on a donc
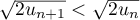 ,
,
soit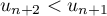 , et la propriété
, et la propriété 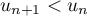 est encore
vraie au rang
est encore
vraie au rang 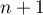 suivant.
suivant.
Conclusion: On vient donc de démontrer, d'après le principe de récurrence, que pour tout entier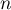 ,
, 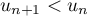 ,
c'est-à-dire que la suite
,
c'est-à-dire que la suite 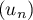 est strictement
croissante.
est strictement
croissante.
2ème méthode: démonstration directe.
Pour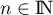 , on a
, on a
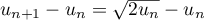 ,
soit, en utilisant la quantité conjuguée:
,
soit, en utilisant la quantité conjuguée:
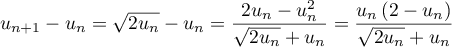
Or, d'après la question précédente,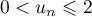 , et donc,
, et donc, 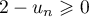 ,
et
,
et 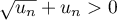 .
.
On a donc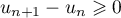 , et la suite
, et la suite 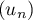 est
donc croissante.
est
donc croissante.
- On vient de prouver la suite
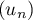 est strictement
croissante et est majorée par 2, on en déduit qu'elle converge
vers une limite réelle
est strictement
croissante et est majorée par 2, on en déduit qu'elle converge
vers une limite réelle 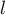 .
.
- Démontrons par récurrence que, pour tout entier naturel
-
- Pour tout entier naturel
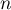 ,
, 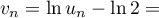 ,
donc,
,
donc,
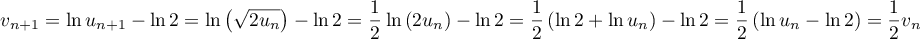
Ainsi,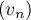 est la suite géométrique de raison
est la suite géométrique de raison  et de 1er terme
et de 1er terme 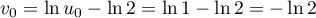 .
.
- On déduit de ce qui précède que pour tout entier naturel
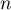 ,
,
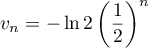 ,
puis que
,
puis que 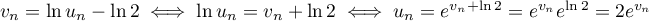 .
.
- Comme
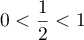 ,
,
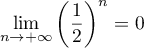 et donc
et donc 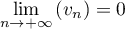 .
.
Comme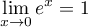 , par composition des limites on obtient:
, par composition des limites on obtient:
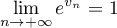 et finalement:
et finalement: 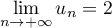 .
.
-

- Pour tout entier naturel
Cacher la correction
Voir aussi: