Exercice corrigé - Deux Suites imbriquées
Exercice corrigé sur les suites
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé sur les suites: deux suites imbriquées définies par récurrence. Utilisation de suites intermédiaires, géométrique et constante, et détermination des expressions explicites, en fonction de n
Exercice - énoncé:
On considère les suites 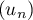 et
et  définies
par leur premier terme
définies
par leur premier terme  et
et 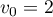 et, pour tout entier
et, pour tout entier 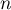 ,
,
![\[\la\begin{array}{ll}
u_{n+1}=\dfrac13u_n+\dfrac23v_n\\[.8em]
v_{n+1}=\dfrac15u_n+\dfrac45v_n\enar\right.\]](/Generateur-Devoirs/1S/Chap9/Suites-Imbriquees/6.png)
Cacher la correction
![\[\la\begin{array}{ll}
u_{n+1}=\dfrac13u_n+\dfrac23v_n\\[.8em]
v_{n+1}=\dfrac15u_n+\dfrac45v_n\enar\right.\]](/Generateur-Devoirs/1S/Chap9/Suites-Imbriquees/6.png)
- Calculer
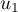 et
et  .
.
- On pose, pout tout entier
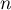 ,
,  .
.
- Calculer
 et
et 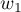 .
.
- Montrer que la suite
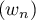 est géométrique.
Préciser sa raison et son premier terme.
est géométrique.
Préciser sa raison et son premier terme.
Donner alors l'expression explicite de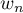 en fonction de
en fonction de  .
.
- Calculer
- On pose, pour tout entier
 ,
,
 .
.
- Calculer
 et
et 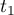 .
.
- Montrer que la suite
 est constante.
est constante.
- Calculer
- Exprimer alors, explicitement en fonction de
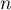 ,
les termes
,
les termes 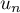 et
et 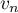 .
.
- Quelles sont les limites de ces deux suites ?
Correction exercice
-
![\[\la\begin{array}{ll}
u_1&=\dfrac13\tm1+\dfrac23\tm2=\dfrac53\\[.8em]
v_1&=\dfrac15\tm1+\dfrac45\tm2=\dfrac95\enar\right.\]](/Generateur-Devoirs/1S/Chap9/Suites-Imbriquees_c/1.png)
- On pose, pout tout entier
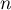 ,
, 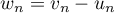 .
.
-
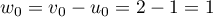 et
et
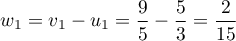
- Pour tout entier
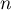 on a,
on a,
![\[\begin{array}{ll}
w_n+1&=v_{n+1}-u_{n+1}\\[.8em]
&=\lp\dfrac15u_n+\dfrac45v_n\rp-\lp\dfrac13u_n+\dfrac23v_n\rp\\[1.2em]
&=-\dfrac2{15}u_n+\dfrac2{15}v_n\\[.8em]
&=\dfrac2{15}\left( v_n-u_n\rp=\dfrac2{15}w_n
\enar\]](/Generateur-Devoirs/1S/Chap9/Suites-Imbriquees_c/7.png)
ce qui montre que cette suite est géométrique de raison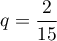 et de premier terme
et de premier terme 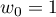 .
.
On a alors directement,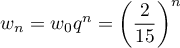 pour tout entier
pour tout entier 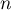 .
.
-
-
-
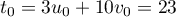 et
et
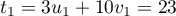 .
.
- Pour tout entier
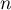 , on a
, on a
![\[\begin{array}{ll}
t_{n+1}&=3u_{n+1}+10v_{n+1}\\[.6em]
&=3\lp\dfrac13u_n+\dfrac23v_n\rp+10\lp\dfrac15u_n+\dfrac45v_n\rp\\[1em]
&=3u_n+10v_n=t_n\enar\]](/Generateur-Devoirs/1S/Chap9/Suites-Imbriquees_c/15.png)
ce qui montre que la suite est constante, égale à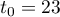 .
.
-
- D'après ce ui précède, on a montré que
![\[\la\begin{array}{ll}
w_n=v_n-u_n=\lp\dfrac2{15}\rp^n\\[1em]
t_n=3u_n+10v_n=23\enar\right.\]](/Generateur-Devoirs/1S/Chap9/Suites-Imbriquees_c/17.png)
On peut résoudre ce système dont les inconnues sont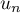 et
et 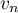 .
.
Par substitution par exemple, la première relation donne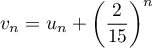 , puis, dans la deuxième relation,
, puis, dans la deuxième relation,
![\[\begin{array}{ll}&3u_n+10v_n=23\\[.6em]
\iff&3u_n+10\left( u_n+\left(\dfrac2{15}\rp^n\rp=23\\[1.2em]
\iff&13u_n=23-10\lp\dfrac2{15}\rp^n\\[1.2em]
\iff&u_n=\dfrac{23}{13}-\dfrac{10}{13}\lp\dfrac2{15}\rp^n\enar\]](/Generateur-Devoirs/1S/Chap9/Suites-Imbriquees_c/21.png)
puis, en reprenant la première relation,
![\[\begin{array}{ll}v_n&=u_n+\lp\dfrac2{15}\rp^n\\[1.2em]
&=\dfrac{23}{13}-\dfrac{10}{13}\lp\dfrac2{15}\rp^n+\lp\dfrac2{15}\rp^n\\[1.2em]
&=\dfrac{23}{13}+\dfrac3{13}\lp\dfrac2{15}\rp^n\enar\]](/Generateur-Devoirs/1S/Chap9/Suites-Imbriquees_c/22.png)
- Comme
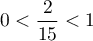 , on a
, on a
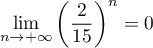 , et alors
, et alors
![\[\lim_{n\to+\infty}u_n=\lim_{n\to+\infty}v_n=\dfrac{23}{13}\]](/Generateur-Devoirs/1S/Chap9/Suites-Imbriquees_c/25.png)
Cacher la correction
Voir aussi: