Exercice corrigé Bac, Nouvelle Calédonie 2014: Suite récurrente
Suites récurrentes - Construction graphique - Algorithme et limite
Exercice corrigé de mathématiques: Exercice corrigé Bac, Nouvelle Calédonie 2014: un exercice complet sur les suites récurrentes, démonstration par récurrence, et algorithme
Exercice - énoncé:
On considère la fonction 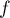 définie sur l'intervalle
définie sur l'intervalle 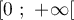 par
par
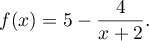
On admettra que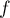 est dérivable sur l'intervalle
est dérivable sur l'intervalle 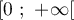 .
.
On a tracé en annexe 1 dans un repère orthonormé la courbe représentative de
représentative de 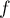 ainsi que la droite
ainsi que la droite 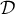 d'équation
d'équation 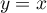 .
.
Annexe 1 à rendre avec la copie
![\psset{unit=1.35cm}
\begin{pspicture}(-0.5,-0.25)(8.1,7.2)
\psaxes[linewidth=1.25pt]{->}(0,0)(-0.5,-0.25)(8.1,7.2)
\psline[linecolor=cyan](7.2,7.2)
\psplot[plotpoints=4000,linewidth=1.25pt,linecolor=blue]{0}{8.1}{5 4 x 2 add div sub}
\uput[dl](0,0){O}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/ex114.NC/45.png)
Annexe 2 à rendre avec la copie

Nouvelle Calédonie, 2014
On considère la fonction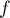 définie sur l'intervalle
définie sur l'intervalle 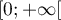 par
par
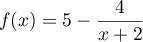 .
.
Annexe
![\psset{unit=1.35cm}
\begin{pspicture}(-0.5,-0.25)(8.1,7.2)
\psaxes[linewidth=1.25pt,arrowsize=2pt 3]{->}(0,0)(-0.5,-0.25)(8.1,7.2)
\psline[linecolor=cyan](7.2,7.2)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{8.1}{5 4 x 2 add div sub}
\uput[dl](0,0){O}
\psset{linecolor=red}
\psline(1,0)(1,3.67)
\psline(0,3.67)(3.67,3.67)
\psline(3.67,0)(3.67,4.294)
\psline(0,4.294)(4.294,4.294)
\psline(4.294,0)(4.294,4.364)
\uput*{8pt}[d](1,0){\red $M_0$}
\uput*{8pt}[d](3.67,0){\red $M_1$} \uput[l](0,3.67){\red $u_1$}
\uput*{8pt}[d](4.294,0){\red $M_2$} \uput[l](0,4.294){\red $u_2$}
\psline[linecolor=blue,linestyle=dashed](4.37,0)(4.37,4.37)
\uput[dr](4.37,0){\blue $\alpha$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/ex114.NC_c/81.png)
Annexe 2

Cacher la correction
On admettra que
On a tracé en annexe 1 dans un repère orthonormé la courbe
- Démontrer que
 est croissante sur l'intervalle
est croissante sur l'intervalle 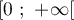 .
.
- Résoudre l'équation
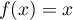 sur l'intervalle
sur l'intervalle 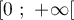 . On note
. On note 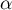 la solution.
la solution.
On donnera la valeur exacte de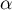 puis on en donnera une valeur approchée à
puis on en donnera une valeur approchée à 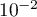 près.
près.
- On considère la suite
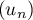 définie par
définie par 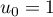 et, pour tout entier naturel
et, pour tout entier naturel 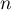 ,
, 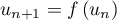 .
.
Sur la figure de annexe 1, en utilisant la courbe et la droite
et la droite  , placer les points
, placer les points  ,
, 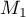 et
et 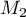 d'ordonnée nulle et d'abscisses respectives
d'ordonnée nulle et d'abscisses respectives 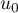 ,
, 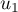 et
et 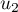 .
.
Quelles conjectures peut-on faire sur le sens de variation et la convergence de la suite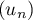 ?
?
-
- Démontrer, par récurrence, que, pour tout entier naturel
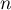 ,
,
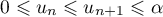
où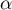 est le réel défini dans la question 2.
est le réel défini dans la question 2.
- Peut-on affirmer que la suite
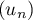 est convergente ? On justifiera la réponse.
est convergente ? On justifiera la réponse.
- Démontrer, par récurrence, que, pour tout entier naturel
- Pour tout entier naturel
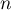 , on définit la suite
, on définit la suite 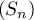 par
par
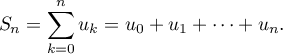
- Calculer
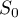 ,
, 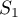 et
et 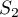 . Donner une valeur approchée des résultats à
. Donner une valeur approchée des résultats à 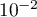 près.
près.
- Compléter l'algorithme donné en annexe 2 pour qu'il affiche la somme
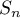 pour la valeur de l'entier
pour la valeur de l'entier 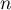 demandée à l'utilisateur.
demandée à l'utilisateur.
- Montrer que la suite
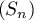 diverge vers
diverge vers 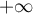 .
.
- Calculer
Annexe 1 à rendre avec la copie
![\psset{unit=1.35cm}
\begin{pspicture}(-0.5,-0.25)(8.1,7.2)
\psaxes[linewidth=1.25pt]{->}(0,0)(-0.5,-0.25)(8.1,7.2)
\psline[linecolor=cyan](7.2,7.2)
\psplot[plotpoints=4000,linewidth=1.25pt,linecolor=blue]{0}{8.1}{5 4 x 2 add div sub}
\uput[dl](0,0){O}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/ex114.NC/45.png)
Annexe 2 à rendre avec la copie

Correction exercice
Nouvelle Calédonie, 2014
On considère la fonction
-
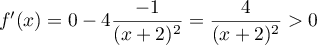 sur
sur 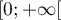 .
.
Donc la fonction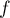 est strictement croissante sur
est strictement croissante sur 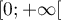 .
.
- On résout dans
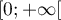 l'équation
l'équation 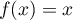 :
:
![$f(x) = x \iff 5-\dfrac{4}{x+2}=x \iff \dfrac{5(x+2)-4 -x(x+2)}{x+2} = 0 \iff
\dfrac{5x+10-4-x^2-2x}{x+2}=0\\[5pt]
\phantom{f(x)=x} \iff \dfrac{-x^2+3x+6}{x+2}=0 \iff
-x^2+3x+6 = 0 \text{ et }x+2 \neq 0](/Generateur-Devoirs/TS/ChapSuites/ex114.NC_c/10.png)
Le trinôme du second degré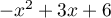 a pour discriminant
a pour discriminant 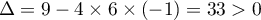 ,
et admet donc 2 solutions réelles:
,
et admet donc 2 solutions réelles: 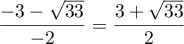 et
et 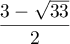 .
.
Cette deuxième solution est négative donc l'unique solution de l'équation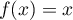 dans l'intervalle
dans l'intervalle 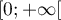 est
est 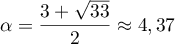 .
.
- On considère la suite
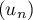 définie par
définie par 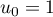 et, pour tout entier naturel
et, pour tout entier naturel 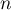 ,
, 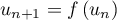 .
.
Sur la figure de annexe 1, on place les points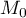 ,
, 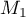 et
et 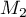 d'ordonnée nulle et d'abscisses respectives
d'ordonnée nulle et d'abscisses respectives 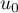 ,
, 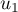 et
et 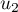 .
.
On peut conjecturer que la suite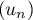 est croissante et converge vers
est croissante et converge vers 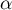 .
.
-
- On cherche à montrer que la propriété
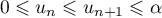 est vraie pour tout entier
est vraie pour tout entier 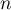 .
.
Initialisation: Pour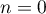 ,
, 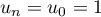 et
et 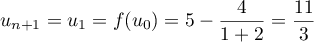 ; de plus
; de plus 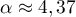 .
On a
.
On a 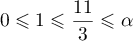 ce qui veut dire que la propriété est vraie au rang 0.
ce qui veut dire que la propriété est vraie au rang 0.
Hérédité: On suppose la propriété vraie au rang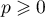 , autrement dit:
, autrement dit: 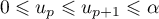 .
.
On sait d'après la question 1. que la fonction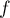 est strictement croissante sur
est strictement croissante sur 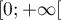 donc:
donc:
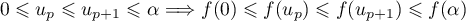
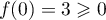 ,
, 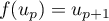 et
et 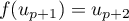 .
.
De plus,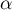 est solution de l'équation
est solution de l'équation 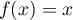 donc
donc 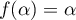 .
.
On a donc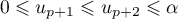 ; on peut dire que la propriété est vraie au rang
; on peut dire que la propriété est vraie au rang 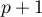 .
.
Conclusion: On a donc démontré d'après le principe de récurrence, que, pour tout entier naturel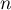 ,
, 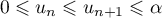 .
.
- Pour tout
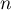 ,
, 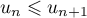 donc la suite
donc la suite 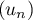 est croissante.
Pour tout
est croissante.
Pour tout 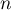 ,
,  donc la suite
donc la suite 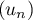 est majorée par
est majorée par 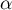 .
.
On en déduit que la suite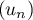 est convergente.
est convergente.
- On cherche à montrer que la propriété
- Pour tout entier naturel
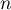 , on définit la suite
, on définit la suite 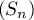 par
par
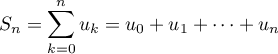 .
.
-
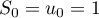 ;
;
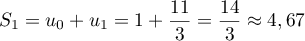
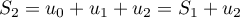 ;
; 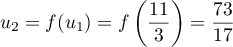 donc
donc
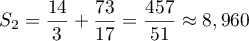 donc
donc 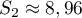 .
.
- On complète l'algorithme donné en annexe 2 pour qu'il affiche la somme
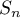 pour la valeur de l'entier
pour la valeur de l'entier 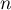 demandée à l'utilisateur.
demandée à l'utilisateur.
- On sait que la suite
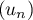 est croissante donc, pour tout
est croissante donc, pour tout 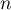 de
de 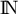 ,
,  .
.
Or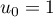 , donc, pour tout
, donc, pour tout 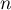 ,
, 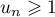 et donc
et donc
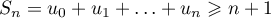 .
Or
.
Or 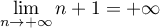 donc, d'après les théorèmes de comparaison sur les limites:
donc, d'après les théorèmes de comparaison sur les limites:
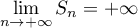
-
Annexe
![\psset{unit=1.35cm}
\begin{pspicture}(-0.5,-0.25)(8.1,7.2)
\psaxes[linewidth=1.25pt,arrowsize=2pt 3]{->}(0,0)(-0.5,-0.25)(8.1,7.2)
\psline[linecolor=cyan](7.2,7.2)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{0}{8.1}{5 4 x 2 add div sub}
\uput[dl](0,0){O}
\psset{linecolor=red}
\psline(1,0)(1,3.67)
\psline(0,3.67)(3.67,3.67)
\psline(3.67,0)(3.67,4.294)
\psline(0,4.294)(4.294,4.294)
\psline(4.294,0)(4.294,4.364)
\uput*{8pt}[d](1,0){\red $M_0$}
\uput*{8pt}[d](3.67,0){\red $M_1$} \uput[l](0,3.67){\red $u_1$}
\uput*{8pt}[d](4.294,0){\red $M_2$} \uput[l](0,4.294){\red $u_2$}
\psline[linecolor=blue,linestyle=dashed](4.37,0)(4.37,4.37)
\uput[dr](4.37,0){\blue $\alpha$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/ex114.NC_c/81.png)
Annexe 2

Cacher la correction
Voir aussi: