Suites récurrentes - Bac Amérique du nord 2013
Calculs à l'aide d'un algorithme et d'une suite intermédiaire logarithmique
On considère la suite
- On considère l'algorithme suivant:
Variables: n est un entier naturel
u est un réel positifInitialisation: Demander la valeur de n
Affecter à u la valeur 1
Traitement: Pour i variant de 1 à n:
— Affecter à u la valeur √2u
Fin de PourSortie: Afficher u - Donner une valeur approchée à 10-4 près du résultat qu'affiche cet algorithme lorsque l'on choisit
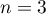 .
.
- Que permet de calculer cet algorithme ?
- Le tableau ci-dessous donne des valeurs approchées obtenues à l'aide de cet algorithme pour certaines valeurs de
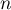 .
.
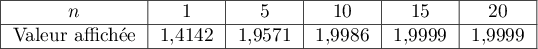
Quelles conjectures peut-on émettre concernant la suite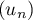 ?
?
- Donner une valeur approchée à 10-4 près du résultat qu'affiche cet algorithme lorsque l'on choisit
-
- Démontrer que, pour tout entier naturel
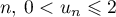 .
.
- Déterminer le sens de variation de la suite
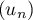 .
.
- Démontrer que la suite
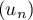 est convergente. On ne demande pas la valeur de sa limite.
est convergente. On ne demande pas la valeur de sa limite.
- Démontrer que, pour tout entier naturel
- On considère la suite
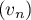 définie, pour tout entier naturel
définie, pour tout entier naturel 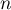 , par
, par 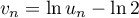 .
.
- Démontrer que la suite
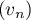 est la suite géométrique de raison
est la suite géométrique de raison  et de premier terme
et de premier terme
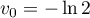 .
.
- Déterminer, pour tout entier naturel
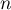 , l'expression de
, l'expression de 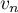 en fonction de
en fonction de 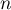 , puis de
, puis de 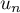 en fonction de
en fonction de 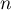 .
.
- Déterminer la limite de la suite
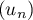 .
.
- Recopier l'algorithme ci-dessous et le compléter par les instructions du traitement et de la sortie, de façon à afficher en sortie la plus petite valeur de
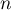 telle que
telle que 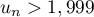 .
.
Variables: n est un entier naturel
u est un réelInitialisation: Affecter à n la valeur 0
Affecter à u la valeur 1
Traitement: Sortie:
- Démontrer que la suite
Voir aussi: